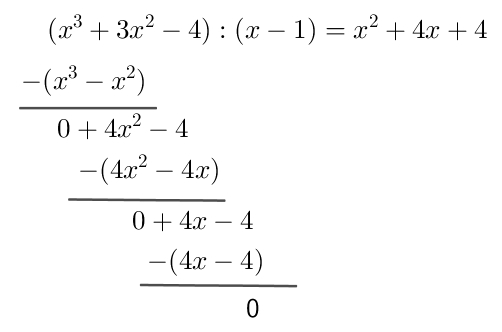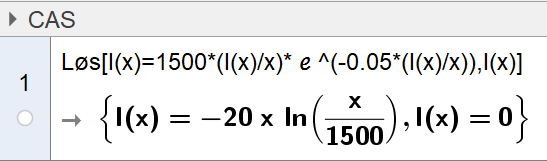S2 2019 høst LØSNING

oppgaven som pdf

diskusjon av oppgaven på matteprat

Løsningsforslag til del 2 laget av mattepratbruker Krisian Saug

Løsningsforslag del 1 og del 2 laget av Svein Arneson

DEL 1

Oppgave 1

a)

$f(x)=\frac{1}{2}\ln x$

$f^{\prime }(x)=\frac{1}{2x}$

b)

$g(x)=3x\cdot e^{2x}$

$$\begin{gathered} g^{\prime }(x)=3\cdot e^{2x}+3x\cdot 2\cdot e^{2x} \\ {g}^{\prime }(x)=3e^{2x}(2x+1) \end{gathered}$$

c)

$h(x)=\frac{x^2+1}{x-3}$

$$\begin{gathered} h^{\prime }(x)=\frac{2x\cdot (x-3)-(x^2+1)\cdot 1}{(x-3{)}^2} \\ {h}^{\prime }(x)=\frac{2x^2-6x-x^2-1}{x^2-6x+9} \\ {h}^{\prime }(x)=\frac{x^2-6x-1}{x^2-6x+9} \end{gathered}$$

Oppgave 2

a)

$$\begin{gathered} a_n=a_1+(n-1)\cdot d \\ {a}_4=a_1+(4-1)\cdot d \\ 7=-8+3d \\ 3d=15 \\ d=5 \end{gathered}$$

$$\begin{gathered} a_n=-8+(n-1)\cdot 5 \\ {a}_n=-8+5n-5 \\ {a}_n=5n-13 \end{gathered}$$

b)

$a_{40}=5\cdot 40-13=200-13=187$

$$\begin{gathered} S_n=\frac{a_1+a_n}{2}\cdot n \\ {S}_{40}=\frac{-8+187}{2}\cdot 40 \\ {S}_{40}=179\cdot 20 \\ {S}_{40}=3580 \end{gathered}$$

Oppgave 3

a)

$a_n=a_1\cdot k^{n-1}$

For denne rekka har vi:

$a_n=6\cdot (-\frac{1}{2}{)}^{n-1}$

Dersom $-1<k<1$ i en geometrisk tallfølge $a_n=a_1{k}^{n-1}$ sier vi at den konvergerer. I dette tilfelle er $k=-\frac{1}{2}$, så rekken konvergerer.

I slike tilfeller er summen $S=\frac{a_1}{1-k}$.

$S=\frac{6}{1-(-\frac{1}{2})}=\frac{6}{\frac{3}{2}}=\frac{6\cdot 2}{3}=4$

b)

$0,135135135...=0,135+1,000135+0,000000135+\dots =\frac{135}{1000}+\frac{135}{{1000}^2}+\frac{135}{{1000}^3}+...$

Dette kan uttrykkes som en geometrisk rekke:

$a_n=\frac{135}{1000}\cdot (\frac{1}{1000}{)}^{n-1}$

Vi har $-1<k<1$, så denne rekken konvergerer. Summen av den geometriske rekken, altså tallet $0,135135135...$ blir da:

$S=\frac{a_1}{1-k}=\frac{\frac{135}{1000}}{1-\frac{1}{1000}}=\frac{\frac{135}{1000}}{\frac{999}{1000}}=\frac{135}{999}=\frac{45}{333}=\frac{15}{111}=\frac{5}{37}$

Det kan være vanskelig å vite at teller og nevner i $\frac{135}{999}$ er delelig på 27, så jeg deler teller og nevner på 3, i tre omganger.

$0,135135135...=\frac{5}{37}$

Oppgave 4

I. $a\cdot x-2y+z=4$

II. $2x+z=6$

III. $3x+3y+z=7$

Setter inn $x=-2$ i likning II.

II. $$\begin{gathered} 2\cdot (-2)+z=6 \\ z=6+4 \\ z=10 \end{gathered}$$

Setter inn $x=-2$ og $z=10$ i likning III.

III. $$\begin{gathered} 3\cdot (-2)+3y+10=7 \\ 3y=7-10+6 \\ y=\frac{3}{3} \\ y=1 \end{gathered}$$

Setter inn $x=-2$, $y=1$ og $z=10$ i likning I.

I. $$\begin{gathered} a\cdot (-2)-2\cdot 1+10=4 \\ -2a=4-10+2 \\ a=\frac{-4}{-2} \\ a=2 \end{gathered}$$

Oppgave 5

$f(x)=x^3+3x^2-4$

a)

$f(x)=x^3+3x^2-4=(x^2+4x+4)(x-1)=(x+2{)}^2\cdot (x-1)$

b)

$f^{\prime }(x)=3x^2+6x=3x(x+2)$

Finner x-verdiene i ekstremalpunktene:

$$\begin{gathered} f^{\prime }(x)=0 \\ 3x(x+2)=0 \\ x=-2\vee x=0 \end{gathered}$$

Finner y-verdiene i ekstremalpunktene:

$f(-2)=(-2{)}^3+3\cdot (-2{)}^2-4=-8+12-4=0$

$f(0)=0^3+3\cdot 0^2-4=-4$

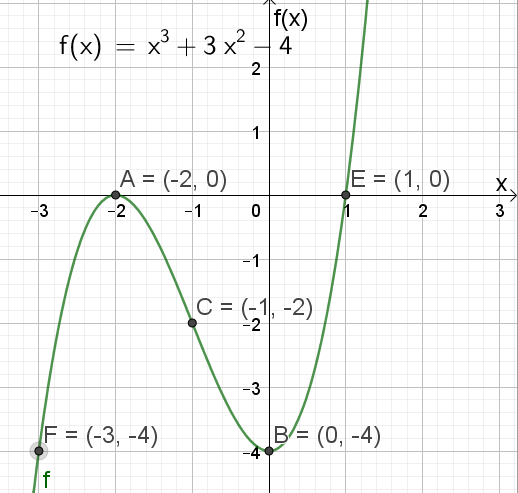
Funksjonen $f$ har et toppunkt i $(-2,0)$ og et bunnpunkt i $(0,-4)$

c)

$f^{\prime }{}^{\prime }(x)=6x+6$

Finner x-verdien i vendepunktet:

$$\begin{gathered} f^{\prime }{}^{\prime }(x)=0 \\ 6x+6=0 \\ x=-1 \end{gathered}$$

Finner y-verdien i vendepunktet:

$f(-1)=(-1{)}^3+3\cdot (-1{)}^2-4=-1+3-4=-2$

Finner den deriverte i vendepunktet:

$a=f^{\prime }(-1)=3\cdot (-1{)}^2+6\cdot (-1)=3-6=-3$

Finner vendetangenten:

$$\begin{gathered} (y-y_1)=a\cdot (x-x_1) \\ y-(-2)=-3(x-(-1)) \\ y+2=-3x-3 \\ y=-3x-5 \end{gathered}$$

d)

Husk at dette må gjøres for hånd på eksamen.

Har ekstremalpunktene A=(-2,0) og B=(0,-4), samt vendepunktet C=(-1, -2) fra før.

Finner f(-3) og f(1) i tillegg.

$f(-3)=(-3{)}^3+3\cdot (-3{)}^2-4=-27+27-4=-4$

$f(1)=1^3+3\cdot 1^2-4=1+3-4=0$

Vi har nå også punktene E=(1,0) og F=(-3,-4). Det holder for en skisse.

e)

Fra før av har vi nullpunktene til funksjonen $f$, A=(-2,0) og E=(1,0). Setter $u=\ln x$.

$$\begin{gathered} (\ln x{)}^3+3(\ln x{)}^2-4=0 \\ {u}^3+3u^2-4=0 \\ u=-2\vee u=1 \end{gathered}$$

$$\begin{gathered} \ln x=-2\vee \ln x=1 \\ x=e^{-2}\vee x=e \end{gathered}$$

Oppgave 6

$h(t)=\frac{100}{1+a\cdot e^{-0,0693\cdot t}}$

a)

$$\begin{gathered} h(0)=20 \\ \frac{100}{1+a\cdot e^{-0,0693\cdot 0}}=20 \\ \frac{100}{1+a\cdot 1}=20 \\ 100=20\cdot (1+a) \\ 100=20+20a \\ a=\frac{80}{20} \\ a=4 \end{gathered}$$

b)

Tallet 100 er den verdien h(t) konvergerer mot når t går mot uendelig. Dette fordi nevneren vil nærme seg 1 når t går mot uendelig (fordi $e^{-\mathrm{\infty }}\approx 0$), og brøken får da tellerens verdi.

Etter mange år vil altså antall gås på øya stabilisere seg på 100.

c)

Siden $h^{\prime }{}^{\prime }(20)=0$, er vendepunktet til funksjonen i $t=20$. Vendepunktet er der veksten er raskest.

Hekkebestanden øker raskest etter 20 år.

Oppgave 7

a)

$E(X)=0\cdot 0,45+1\cdot 0,30+2\cdot 0,10+3\cdot 0,10+4\cdot 0,05=0,30+0,20+0,30+0,20=1$

E(X) forteller oss at vi kan forvente 1 skade på et tilfeldig valgt epletre.

b)

$$\begin{gathered} VAR(X)=(0-1{)}^2\cdot 0,45+(1-1{)}^2\cdot 0,30+(2-1{)}^2\cdot 0,10+(3-1{)}^2\cdot 0,10+(4-1{)}^2\cdot 0,05 \\ =0,45+0,10+0,40+0,45=1,4 \end{gathered}$$

c)

S er summen av X antall skader på 400 uavhengige tilfeldige valg av trær. Sentralgrensesetningen sier at for et stort antall forsøk (slik som 400) er S tilnærmet normalfordelt.

$E(S)=n\cdot E(X)=400\cdot 1=400$

$STDAV(S)=\sqrt{400}\cdot STDAV(X)=\sqrt{400}\cdot \sqrt{VAR(X)}=\sqrt{400}\cdot \sqrt{1,4}$

$VAR(S)=(STDAV(S){)}^2=400\cdot 1,4=560$

d)

$x=50\cdot 1,2=60$

$z=\frac{x-\mu }{\sigma }=\frac{60-50}{8}=\frac{10}{8}=\frac{5}{4}=1,25$

$P(Z\ge 1,25)=1-P(Z\le 1,25)=1-0,8944=0,1056$

Det er 10,56% sannsynlighet for at denne eplegården må sette i verk tiltak dersom de får tilsyn.

DEL 2

Oppgave 1

a)

La x være antall kalkuner, y være antall griser, og z være antall juletrær.

$x+y+z=1284$

$2x+4y+z=2599$

$x=2(y+z)$

b)

Det er 153 griser på gården.

Oppgave 2

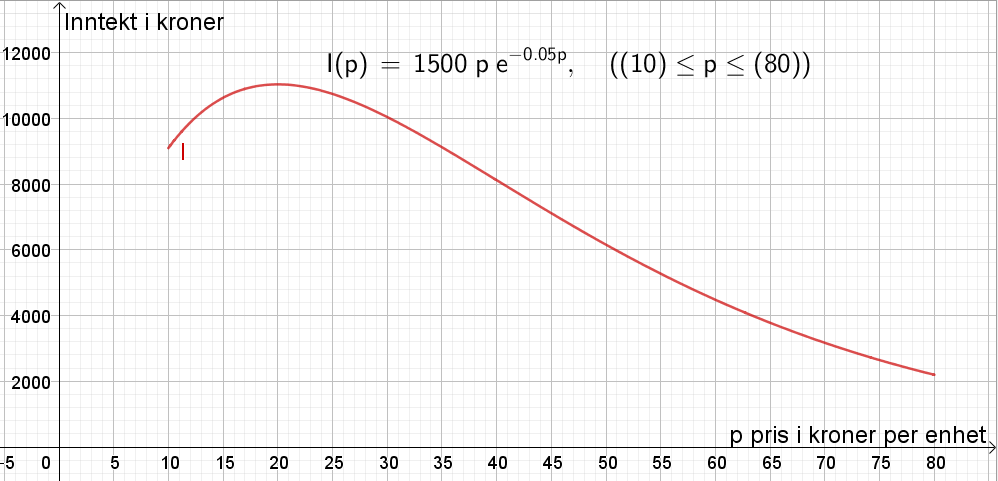
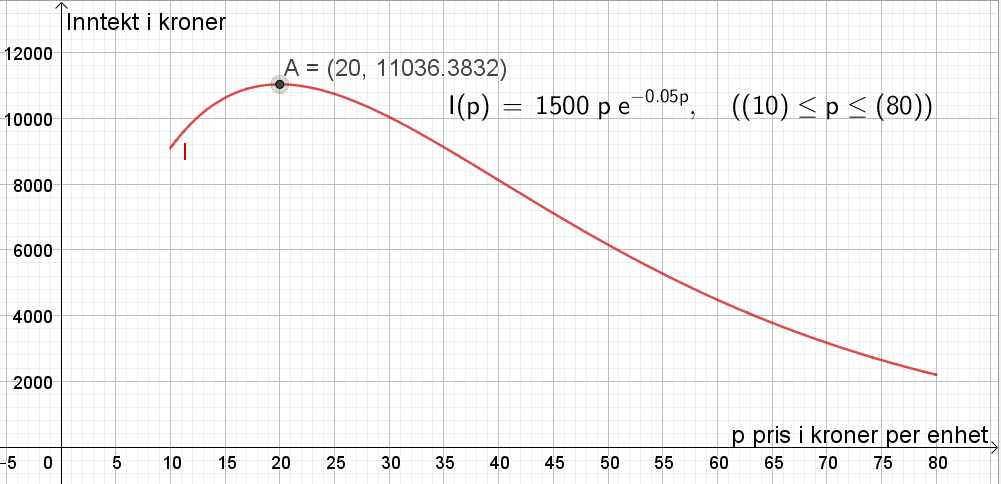
$I(p)=1500p\cdot e^{-0.05p},p\in [10,80]$

a)

Tegner grafen til $I$ i Geogebra.

b)

Bruker kommandoen Ekstremalpunkt[funksjon, start, slutt] og skriver Ekstremalpunkt[I,10,80]. Får punkt A=(20, 11036).

Den prisen som gir høyest inntekt er 20 kroner per enhet.

c)

Pris per enhet ganger antall solgte enheter gir oss den totale inntekten.

$$\begin{gathered} p\cdot x=I(x) \\ p=\frac{I(x)}{x} \end{gathered}$$

Setter inn $\frac{I(x)}{x}$ for p, i funksjonen $I(p)$

Får da:

$I(x)=1500\cdot \frac{I(x)}{x}\cdot e^{-0.05\frac{I(x)}{x}}$

Løser dette i CAS i Geogebra:

Svaret står ikke på samme måte som det vi skulle vise, men vi kan omforme det ved hjelp av logaritmereglene:

$-20x\cdot ln(\frac{x}{1500})=-20x\cdot (ln(x)-ln(1500))=-20x\cdot ln(x)+20x\cdot ln(1500)=20x\cdot (ln(1500)-lnx)=20x\cdot ln(\frac{1500}{x})$

Vi har nå vist at $I(x)=20x\cdot ln(\frac{1500}{x})$

d)

Kostnaden for x produserte enheter per uke kan uttrykkes ved:

$K(x)=15x+2000$

Overskuddet per uke kan uttrykkes ved:

$O(x)=I(x)-K(x)$

Bruker CAS i Geogebra til å finne et uttrykk for O (linje 3), og ekstremalpunktet til O (linje 4). Sjekker også at ekstremalpunktet er et toppunkt, ved å sjekke at funksjonen vokser før ekstremalpunktet, og synker etter ekstremalpunktet (linje 5 og 6).

Det største overskuddet bedriften kan få per uke er ca. 3212,22 kr.

Oppgave 3

a)

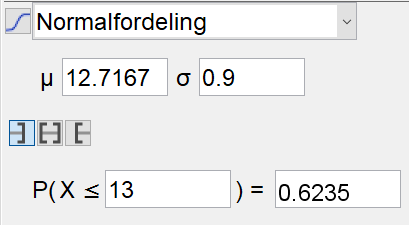
$\mu =12+\frac{43}{60}=12,7167$ min

$\sigma =\frac{54}{60}=0,9$ min

Bruker sannsynlighetskalkulatoren i Geogebra.

Sannsynligheten for at en tilfeldig valgt gutt greier tidskravet på 3000-meterløpet er 0,6235.

b)

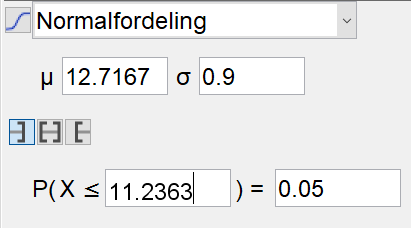
Bruker sannsynlighetskalkulatoren i Geogebra, og fyller ut en sannsynlighet på 0,05.

Vi finner ut at Pål må løpe på 11,2363 min. $0,2363\cdot 60=14,178$ sekunder.

Pål må løpe på under 11 minutter og 14 sekunder.

c)

Setter opp en nullhypotese om at en gutt løper på tidskravet.

$H_0:\mu =12,7167$ min

Alternativ hypotese er at en gutt løper raskere enn tidskravet.

$H_1:\mu <12,7167$

d)

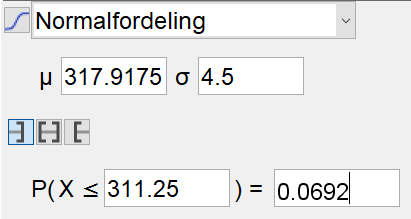
Ifølge sentralgrensesetningen er summen av tidene til de 25 guttene normalfordelt med:

$\mu =12,7167\cdot 25=317,9175$ min

$\sigma =0,9\cdot \sqrt{25}=4,5$ min

Gjennomsnittstiden for de 25 guttene er: $12+\frac{27}{60}=12,45$ min

Sumtiden for de 25 guttene er: $12,45\cdot 25=311,25$ min

Bruker sannsynlighetskalkulatoren i Geogebra for å finne sannsynligheten for at sumtiden for de 25 guttene er på 311,25 min når sumtiden er normalfordelt med forventningsverdi 317,9175 min og standardavvik på 4,5 min.

Sannsynligheten for dette er 6,92%, som er større enn signifikansnivået på 5%. Det er altså ikke grunnlag for å si at treningsprogrammet har god effekt.