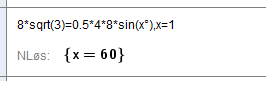1T 2021 vår K06 LØSNING

26.05.2021 MAT1013 Matematikk 1T Kunnskapsløftet K06

Oppgaven som pdf

Diskusjon av oppgaven på matteprat

Løsningsforslag laget av Marius Nilsen ved Bergen Private Gymnas

Videoløsningsforslag del 1 av Lektor Lainz

Oppgave 1

$\left[\begin{array}{r}2x-y=4\\ x-2y=5\end{array}\right]$

$\left[\begin{array}{r}2x-y=4\\ x=2y+5\end{array}\right]$

$\left[\begin{array}{r}2(2y+5)-y=4\\ x=2y+5\end{array}\right]$

$\left[\begin{array}{r}3y=-6\\ x=2y+5\end{array}\right]$

$\left[\begin{array}{r}y=-2\\ x=1\end{array}\right]$

Oppgave 2

Sin(60)

$(\frac{3}{4}{)}^{-1}=\frac{4}{3}$

$Sin({160}^{\circ })=sin({20}^{\circ })$

lg(1) = 0

Sinus avleses på y aksen i enhetssirkelen og er positiv i første og andre kvadrant. Sin(60) > Sin(20).

Vi får i stigende rekkefølge

lg (1) , $sin({160}^{\circ })$ , $sin({60}^{\circ })$ , $(\frac{3}{4}{)}^{-1}$

Oppgave 3

$\frac{x}{x-3}+\frac{x-6}{x+3}-\frac{18}{x^2-9}=\frac{x(x+3)+(x-6)(x-3)-18}{(x-3)(x+3)}=\frac{x^2+3x+x^2-9x+18-18}{(x-3)(x+3)}=\frac{2x^2-6x}{(x-3)(x+3)}=\frac{2x(x-3)}{(x-3)(x+3)}=\frac{2x}{x+3}$

Oppgave 4

$f(x)=(x+4)(x-2)=x^2+2x-8$

En ulikhet som har løsningsmengde $x\in [-4,2]$ er: $f(x)\le 0$

Oppgave 5

Grafen er symmetrisk om y aksen og er -2 når x= 0:

$f(x)=a{x}^2-2$

f(2)= 2 betyr at a = 1. Altså er funksjonsuttrykket $f(x)=x^2-2$

Oppgave 6

$f(x)=-2x+9$

g er parallell med f, dvs den har stigningstall -2.

g(x) = -2x +b

g går gjennom punktet (20, -72):

$$\begin{gathered} -72=-2\cdot 20+b \\ b=-32 \end{gathered}$$

g(x) = -2x - 32

Oppgave 7

$3^{-2}\frac{a^{\frac{1}{4}}\cdot \sqrt{a^3}}{(a^{\frac{3}{4}}{)}^3\cdot a^0}=\frac{1}{9}\cdot a^{\frac{1}{4}+\frac{3}{2}-\frac{9}{4}-0}=\frac{1}{9}{a}^{-\frac{1}{2}}$

a)

$$\begin{gathered} 3^{2x+2}=81 \\ {3}^{2x+2}=9^2 \\ {3}^{2x+2}=3^4 \\ 2x+2=4 \\ x=1 \end{gathered}$$

b)

$$\begin{gathered} lg(\frac{1}{2x+2})=-2 \\ {10}^{lg(\frac{1}{2x+2})}={10}^{-2} \\ \frac{1}{2x+2}=\frac{1}{100} \\ 2x+2=100 \\ x=49 \end{gathered}$$

a)

	Fornøyd	Ikke Fornøyd	Sum
VG 1	$48$	$72$	$120$
VG 3	$90$	$60$	$150$
Sum	$138$	$132$	$270$

b)

Tilfeldig elev fornøyd. $P(F)=\frac{138}{270}=0,5$

Oppgave 10

Bruker arealsetningen: $A=\frac{1}{2}ab\cdot sin(v)$

$$\begin{gathered} 15=\frac{1}{2}\cdot 5\cdot 15\cdot sin(v) \\ 30=60\cdot sin(v) \\ sin(v)=\frac{1}{2} \\ v={30}^{\circ } \end{gathered}$$

Oppgave 11

Posen er 1 kg. Vekt sjokolade = x. Vekt marsipan = y.

$x+y=1$

Det koster 116 kroner å lage en pose ( 166 kr gir 50 kroner i forteneste.:

$$\begin{gathered} 100x+140y=116 \\ 100x+140(1-x)=116 \\ -40x=-24 \\ x=0,6 \end{gathered}$$

Det er 600 gram marsipan, og 400 gram sjokolade i posen.

Oppgave 12

Setter sidekanten i kvadratene lik 1.

Finner cos(v) ved å bruke Pytagoras og definisjon av cosinus: $cos(v)=\frac{3}{\sqrt{10}}$

Finner cos(u) ved å bruke cosinussetningen og Pytagoras:

$$\begin{gathered} a^2=b^2+c^2-2bc\cdot cos(A) \\ cos(u)=\frac{1-(\sqrt{5}{)}^2-(\sqrt{8}{)}^2}{-2\cdot \sqrt{5}\sqrt{8}}=\frac{1-5-8}{-4\sqrt{5}\sqrt{2}}=\frac{3}{\sqrt{10}} \end{gathered}$$

Oppgave 13

Momentan vekst i (3, f(3))

$$\begin{gathered} f(x)=x^3-2x^2-4x+8 \\ {f}^{\prime }(x)=3x^2-4x-4 \\ {f}^{\prime }(3)=27-12-4=11 \end{gathered}$$

Gjennomsnittlig vekst i [-3, 0]: $\frac{f(0)-f(-3)}{3}=\frac{8-(-27-18+12+8)}{3}=\frac{33}{3}=11$

Oppgave 14

$f(x)=x^2+21$

Høyden i rektangelet er f(x). Bredden av rektangelet er (12 - x).

Arealet av rektangelet er $A(x)=f(x)(12-x)=(x^2+21)(12-x)=12x^2-x^3+252-21x=-x^3+12x^2-21x+252$

Deriverer:

$(A(x){)}^{\prime }=-3x^2+24x-21$

Finner den x verdi hvor A er størst, ved å sette den deriverte lik null: $$\begin{gathered} -3x^2+24x-21=0 \\ -3(x^2-8x+7)=0 \\ -3x(x-1)(x-7)=0 \\ x=1\vee x=7 \end{gathered}$$

Den deriverte vender sin hule side ned, maksimumspunktet vil derfor være for x=7.

$A(7)=-(7^3)+12\cdot 7^2-21\cdot 7+252=350$

Oppgave 1

a)

b)

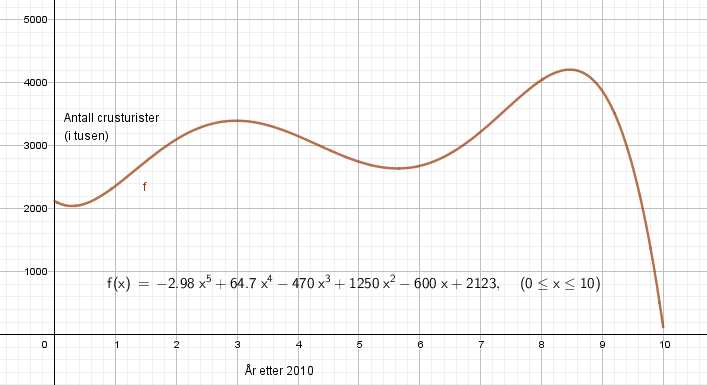
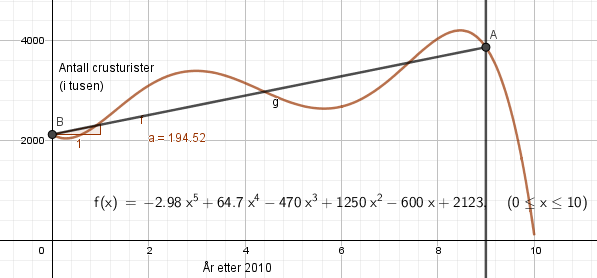
Stigningstallet er 194,5. Det betyr at antall cruiseturister i perioden 2010-2019 økte i gjennomsnitt med ca. 194 500 per år.

c)

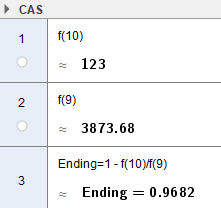
Nedgangen var på nesten 97%.

Oppgave 2

Ut fra gitt informasjon er det naturlig å prøve seg med arealsetningen. Innsatt i CAS:

Vinkelen mellom sidene i trekanten er 60 grader. Da vet vi også at en vinkel på 180 - 60 = 120 grader også tilfredsstiller betingelsene.

Oppgave 3

Dersom han trekker uten tilbakelegging:

P(to av samme farge:) = P(to hvite) + P( to røde) =$\frac{6}{16}\cdot \frac{5}{15}+\frac{10}{16}\cdot \frac{9}{15}=\frac{24}{48}=0,5$ = 50%

Vel dersom det er 50% sannsynlig at man trekker to drops med lik farge, må resten av mulighetene være ulik farge, altså 50% for det også.

Trekning med tilbakeligging:

P(to av samme farge:) = P(to hvite) + P( to røde) =$\frac{6}{16}\cdot \frac{6}{16}+\frac{10}{16}\cdot \frac{10}{16}=\frac{36+100}{256}=0,53$ = 53%

Med tilbakelegging er ikke sannsynligheten for to like farger den samme som for to ulike farger. Detter er en svakhet med oppgaven og trekningsmetode burde vært presisert.

=a)

Et rektangel som har en bredde på n enheter og en lengde på (n+1) enheter vil bestå av n(n+1) enheter. Deler man rektangelet diagonalt i to like store trekanter får man:

$T_n=\frac{n(n+1}{2}$