2P 2021 vår LØSNING

Oppgaven som pdf

Diskusjon av oppgaven på matteprat

Løsningsforslag laget av Marius Nilsen ved Bergen Private Gymnas

Videoløsninger til del 1 laget av Lektor Håkon Raustøl

Oppgave 1

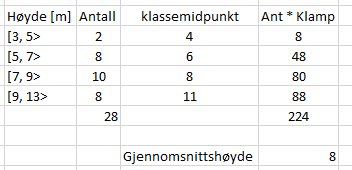
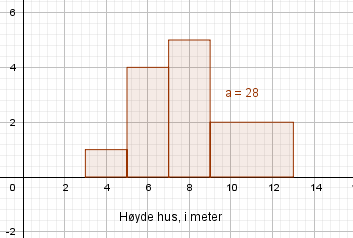
0,0,0,0, 4, 13, 15,17,20,26

Median er (4+13)/2 = 8,5.

Typetall er 0.

Gjennomsnitt er 95/10 = 9,5

Variasjonsbredde er 26 - 0 = 26.

Oppgave 2

Vi gjør alt om til standardform:

250 millioner = $2,5\cdot {10}^8$

$0,25\cdot {10}^{10}=2,5\cdot {10}^9$

$2500\cdot {10}^7=2,5\cdot {10}^{10}$

$0,250\cdot {10}^{-5}=2,5\cdot {10}^{-6}$

$0,025\cdot {10}^{-2}=2,5\cdot {10}^{-4}$

$0,0025\mathrm{\%}=\frac{0,0025}{100}=0,000025=2,5\cdot {10}^{-5}$

Da er det bare å ta utgangspunkt i eksponentene for å få stigende rekkefølge.

$0,250\cdot {10}^{-5}=2,5\cdot {10}^{-6}$

$0,0025\mathrm{\%}=\frac{0,0025}{100}=0,000025=2,5\cdot {10}^{-5}$

$0,025\cdot {10}^{-2}=2,5\cdot {10}^{-4}$

250 millioner = $2,5\cdot {10}^8$

$0,25\cdot {10}^{10}=2,5\cdot {10}^9$

$2500\cdot {10}^7=2,5\cdot {10}^{10}$

Oppgave 3

$(x\cdot 0,9)\cdot 0,8=720$

$0,72x=720$

$x=\frac{720}{0,72}=1000$

Varen kostet 1000 kroner før første nedsettelse.

Oppgave 4

a)

$P(x)=\frac{3000}{x}+100$

b)

$P(x)=130$

$130=\frac{3000}{x}+100$

$130x-100x=3000$

x =100

For at prisen skal bli lavere enn 130 kroner, må minst 101 personer komme på avslutningen.

Oppgave 5

a)

b)

Oppgave 6

a)

Dersom en størrelse forandrer seg med en gitt prosent hver eneste tidsperiode har man en situasjon med eksponentiell vekst. Bakterier kan vokse tilnærmet eksponentielt.

b)

I en bakteriekultur er det 50 000 bakterier. Kulturen vokser med 5% per time. Hvor lang tid tar det før man har 1 000 000 bakterier?

Kan løses på mange måter. Grafisk: tegn $f(x)=50000\cdot 1,{05}^x$ og y= 1 000 000 i samme koordinatsystem og finn skjæring.

Oppgave 7

a)

b)

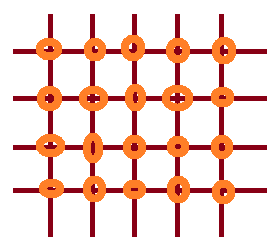
I figur 10 vil det vøre 10 + 9 pinner, altså 19. Det vil være 10 ganger 9 kuler, altså 90.

c)

Pinner: $P(n)=n+(n-1)=2n-1$.

Kuler: $K(n)=n\cdot (n-1)=n^2-n$