R2 2023 høst LØSNING

Oppgaven som PDF

Løsningsforslag fra Lektor Seland

Videoløsning del 1 av Lektor Lainz

Videoløsning del 2 av Lektor Lainz

Løsningsforslag laget av OpenMathBooks prosjektet

DEL 1

Oppgave 1

${\int }_{-1}^1(x^3+2x)dx$

$=[\frac{1}{4}{x}^4+x^2{]}_{-1}^1$

$=(\frac{1}{4}+1)-(\frac{1}{4}+1)=0$

Svaret forteller meg enten at arealet av området som er avgrenset av grafen, x-aksen og linjene x = −1 og x = 1 er lik 0, eller at det er et like stort område over og under x-aksen i dette intervallet. Det er det siste som er tilfellet her.

Oppgave 2

Den blå grafen er g(x)=sin x, fordi sin(0)=0. Den rød grafen er da f(x)=cos x, og den krysser y-aksen i y=1 fordi cos(0)=1.

Skjæringspunkt mellom f og g:

$sinx=cosx$

$x=\frac{\pi }{4}+k\pi$

Skjæringspunktene mellom f og g i det fargelagte området:

$x=-\frac{3\pi }{4}$ og $x=\frac{\pi }{4}$

Areal av det fargelagte området:

${\int }_{-\frac{3\pi }{4}}^{\frac{\pi }{4}}cosxdx-{\int }_{-\frac{3\pi }{4}}^{\frac{\pi }{4}}sinxdx$

$=(sin(\frac{\pi }{4})-sin(-\frac{3\pi }{4})-(-cos(\frac{\pi }{4})+cos(-\frac{3\pi }{4}))$

$=\frac{\sqrt{2}}{2}-(-\frac{\sqrt{2}}{2})-(-\frac{\sqrt{2}}{2}+(-\frac{\sqrt{2}}{2}))$

$=2\frac{\sqrt{2}}{2}+2\frac{\sqrt{2}}{2}=4\frac{\sqrt{2}}{2}=2\sqrt{2}$

Arealet av det fargelagte området vist på figuren er $2\sqrt{2}$.

Oppgave 3

a)

$S=\frac{a_1}{1-k}$

Siden rekken konverger mot 8 må k være $\frac{1}{2}$ :

$8=\frac{4}{1-k}\Rightarrow k=\frac{1}{2}$

$S_4=4+2+1+\frac{1}{2}=7,5$

b)

I en aritmetisk rekke øker leddene med en fast verdi d.

$a_1=a_4-3d$

$a_7=a_4+3d$

$a_1+a_4+a_7=114$

$a_4-3d+a_4+a_4+3d=114$

$3a_4=114$

$a_4=38$

Oppgave 4

a)

Vi har $\alpha :x-2y+2z+1=0$ og $A(4,2,2)$

${\overrightarrow{n}}_{\alpha }=[1,-2,2]$

$l=\{\begin{array}{l}x=4+t\\ y=2-2t\\ z=2+2t\end{array}$

b)

$d=\frac{|a{x}_0+b{y}_0+c{z}_0+d|}{\sqrt{a^2+b^2+c^2}}$, der $(x_0,y_0,z_0)$ er koordinatene til punkt A.

$=\frac{1\cdot 4-2\cdot 2+2\cdot 2+1}{\sqrt{1^2+(-2{)}^2+2^2}}$

$=\frac{5}{\sqrt{9}}=\frac{5}{3}$

Asvtanden fra A til $\alpha$ er $\frac{5}{3}$

Oppgave 5

a)

Programmet regner ut arealet av flaten som er avgrenset av f(x), x- aksen, linjen x = -2 og linjen x = 2.

b)

$f(x)=x^2-1$

Funksjonen har nullpunkter for x=-1 og x= 1. Mellom disse ligger den under x aksen. Den er symmetrisk om y-aksen. Vi integrerer fra -2 til -1 og fra -1 til 0. Til slutt multipliserer vi med 2, for å finne hele arealet.

$A=2\cdot ({\int }_{-2}^{-1}(x^2-1)dx+|{\int }_{-1}^{-0}(x^2-1))dx|$

$=2\cdot ([\frac{1}{3}{x}^3-x{]}_{-2}^{-1}+|[\frac{1}{3}{x}^3-x{]}_{-1}^0)|$

$=2\cdot ((\frac{-1}{3}+1)-(\frac{-8}{3}+2)+|((0)-(\frac{-1}{3}+1)|$

$=2\cdot (\frac{4}{3}+\frac{2}{3})$

$=2\cdot \frac{6}{3}$

$=4$

Oppgave 6

Arealet av sideflaten BCGF er

$\frac{1}{2}|\overrightarrow{BF}\times \overrightarrow{BC}|+\frac{1}{2}|\overrightarrow{GF}\times \overrightarrow{GC}|$

Regner ut $\overrightarrow{BF}\times \overrightarrow{BC}$

$=\left|\begin{array}{ccc}\overrightarrow{i}& \overrightarrow{j}& \overrightarrow{k}\\ -1& -1& 3\\ -4& 0& 0\end{array}\right|$

$=0\overrightarrow{i}-12\overrightarrow{j}-4\overrightarrow{k}$

$=[0,-12,-4]$

Regner ut $\overrightarrow{GF}\times \overrightarrow{GC}$

$=\left|\begin{array}{ccc}\overrightarrow{i}& \overrightarrow{j}& \overrightarrow{k}\\ 2& 0& 0\\ -1& 1& -3\end{array}\right|$

$=0\overrightarrow{i}+6\overrightarrow{j}+2\overrightarrow{k}$

$=[0,6,2]$

Arealet av sideflaten BCGF er

$\frac{1}{2}|\overrightarrow{BF}\times \overrightarrow{BC}|+\frac{1}{2}|\overrightarrow{GF}\times \overrightarrow{GC}|$

$\frac{1}{2}|[0,-12,-4]|+\frac{1}{2}|[0,6,2]|$

$=\frac{1}{2}\sqrt{0^2+{12}^2+4^2}+\frac{1}{2}\sqrt{0^2+6^2+2^2}$

$=\frac{1}{2}\sqrt{160}+\frac{1}{2}\sqrt{40}$

$=\frac{1}{2}\cdot 4\sqrt{10}+\frac{1}{2}\cdot 2\sqrt{10}$

$=3\sqrt{10}$

DEL 2

Oppgave 2

a)

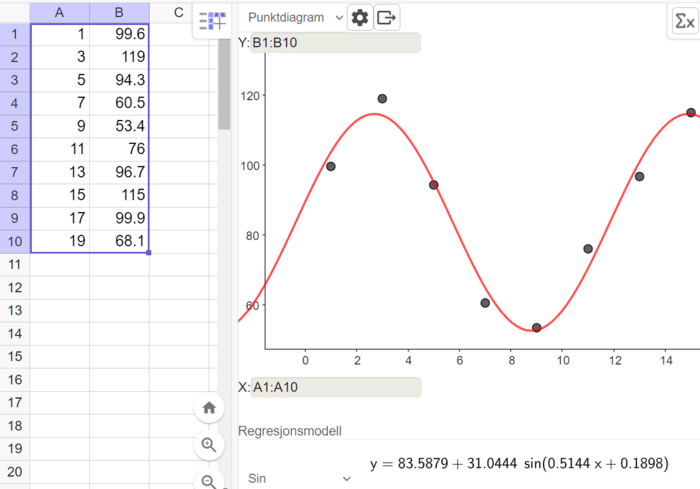
Bruker regresjonsanalyse i Geogebra og velger en sinusfunksjon som modell.

Modellen for vannstanden ved verftet er $f(x)=31sin(0,514x+0,19)+83,6$