1T 2024 høst LØSNING

Oppgaven som pdf

Diskusjon av oppgaven på matteprat

DEL EN

Oppgave 1

$u={30}^{\circ }$

$2\cdot \sin (u)\cdot \cos (u)=2\cdot \frac{1}{2}\cdot \frac{\sqrt{3}}{2}=\frac{\sqrt{3}}{2}$

2u blir 60 grader og fra figuren ser vi at $\sin (2u)=\sin ({60}^{\circ })=\frac{\sqrt{3}}{2}$ så formelen stemmer.

Oppgave 2

Vi ser at dette er en andregradsfunksjon med nullpunkter for x= -3 og x = 1. Vi har symmetri så funksjonen vil ha sin laveste verdi når x = -1.

$f(-1)=(-1-1)(-1+3)=-2\cdot 2=-4$

Bunnpunkt (-1, 4)

Oppgave 3

Vi utfører en polynom divisjon for å faktorisere uttrykket.

Vi observerer at f(1) = 0, da er f delelig med (x-1).

$(x^3+7x^2+4x-12):(x-1)=x^2+8x+12$

$-(x^3-x^2)$

$8x^2+4x-12$

$-(8x^2-8x)$

$12x-12$

$-(12x-12)$

$0$

Så faktoriserer vi andregradsuttrykket:

Bruker ABC formelen og finner at $x_1=-6\vee x_2=-2$

Da har vi at $x^3+7x^2+4x-12=(x-1)(x+2)(x+6)$

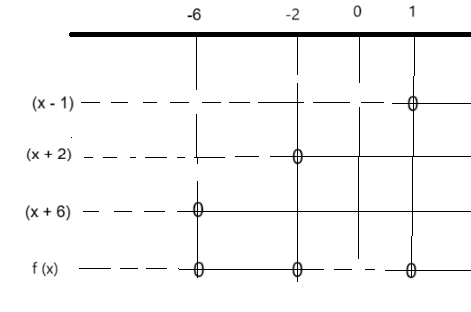
Så lager vi et fortegnsskjema for å finne ut for hvilke verdier f(x) er negativ, null og positiv:

Da har vi et fortegnsskjema som viser når f er positiv og negativ. Dette stemmer med grafen nedenfor.

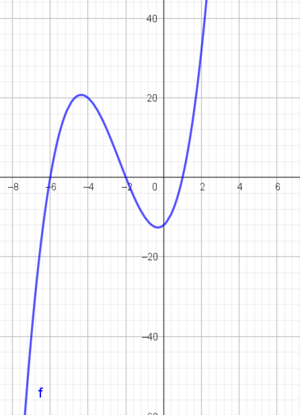
Da gjennstår det bare å se på $f(x)<0:$

f skal være mindre enn null. Det er den i området fra minus uendelig til -6 og mellom -2 og 1.

$x\in <\leftarrow ,-6>\cup <-2,1>$

Oppgave 4

a)

Tangens er sinus delt på cosinus. Tangens til 50 grader er større enn en fordi $\frac{0,77}{0,64}$ er større enn 1.

b)

Vinkelen befinner seg i andre kvadrant der cosinus er negativ og sinus positiv. Da er tangens negativ, altså mindre enn null.

Oppgave 5

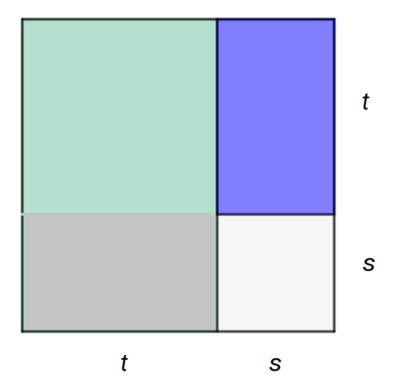
Arealet av det store kvadratet:

$(t+s)(t+s)=t^2+2ts+s^2$

Dette er en matematisk identitet, 1. kvadratsetning. Det andre leddet på høyre side, 2ts er arealet av de to rektangelene i fuguren, som begge har areal t ganger s.

DEL TO

Oppgave 1

a)

Abbonenter i 2010:

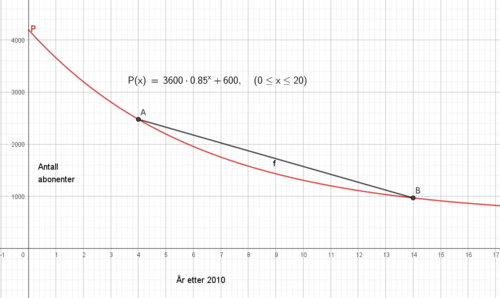
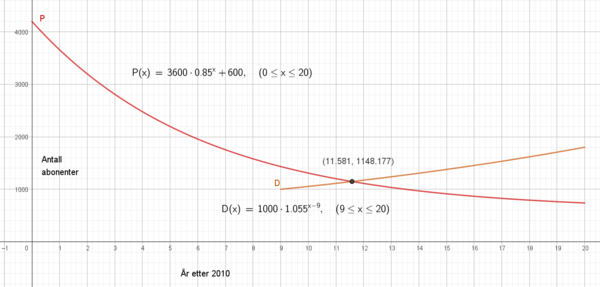
$P(0)=3600+600=4200$, eller man kan lese av grafen på y aksen og få samme resultat.

b)

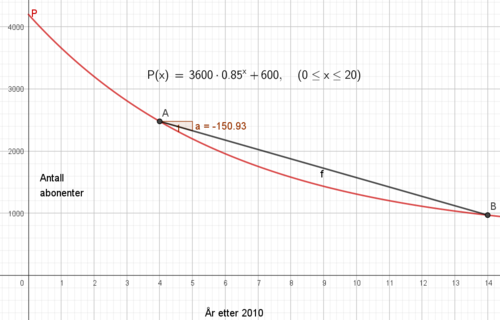
Mellom 2014 og 2024 mister avisen i gjennomsnitt 151 papir abonnenter per år.

c)

Dersom vi regner origo som 1. januar 2010 vi antall digitalabonnenter passere papirabonnentene på sommeren i 2021.

Oppgave 2

Vi har 12 likesidede trekanter. Vi bruker arealsetningen på en enkelt trekant og multipliserer med tolv, for å få arealet av hele stjernen: Alle sider i de små trekantene er 4 og alle vinkler er 60 grader.

$12A=12\cdot \frac{1}{2}\cdot 4\cdot 4\cdot \frac{\sqrt{3}}{2}=48\sqrt{3}$

Oppgave 3

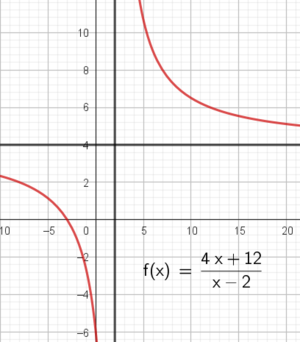
For vertikal asymptote i 2, må nevner bli null for x=2.

Når x = - 3 må telleren bli null (nullpunkt). I tillegg må hele brøken gå mot 4 når x går mot uendelig.

Oppgave 4

a)

b)

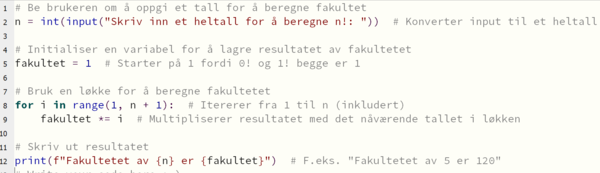
100! er et stort tall. For at et tall skal slutte på null må det ha en faktor 10 i seg. For at det skal slutte på 00 - to nuller, ma det ha en faktor 10 i seg to ganger. Tallet 10 kan faktorisers til faktorene 5 og 2. Faktoren 2 finnes mange ganger i 100!, den er jo en faktor i alle partall. Hvor mange ganger finner man faktoren 5?

Dersom vi deler 100 på 5 får vi 20: 5, 10, 15,.............. 95, 100

Tall som 25, 50 75 og 100 bidrar med to femmerfaktorer.

Vi får da: $\frac{100}{5^1}+\frac{100}{5^2}=20+4=24$

(Det minste tallet som bidrar med tre femmerfaktorer er 125, men det er jo ikke med.)

Oppgave 5

På linje 1 defineres f.

På linje 2 bruker man opplysningen om punktet (2,6)

På linje 3 bruker vi informasjon om koordinatene til toppunktet. Det andre kulepunktet i oppgaven inneholder dobbel informasjon: vi vet også at den deriverte er null når x = -2. Den informasjonen bruker vi i linje 4.

Informasjon om tangentens stigningstall i (3, f(3)) er brukt i linje 5.

Vi har nå fire likninger og fire ukjente og løser.

Oppgave 6

a)

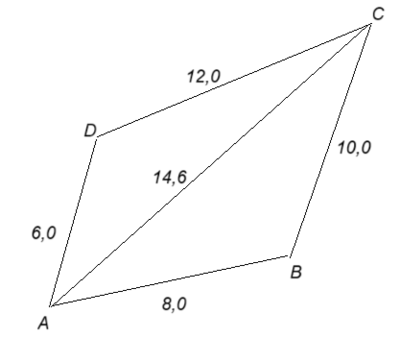
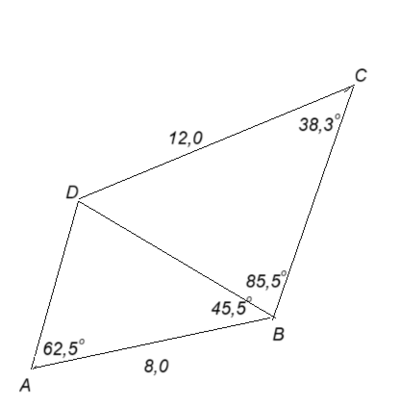
Vi kan se på firkanten ABCD som to trekanter som ligger inntil hverandre, ACD og ABC. Vi kjenner alle sidene i trekantene og bruker Cosinussetningen for å finne en vinkel i hver trekant. Så bruker vi arealsetningen på hver av trekantene og legger sammen. For å bruke arealsetningen trenger vi to sider i trekanten og vinkelen mellom dem.

b)

Diagonalen BD deler firkanten opp i to nye trekanter hvor alle vinkler er kjent (Den tredje vinkelen i en trekant finner du ved å ta 180 minus de to du allerede kjenner.). Bruk sinussetningen til å finne en side, for eksempel BD (sparer arbeid, da denne er en side i begge trekantene). Du kan nå bruke arealsetningen og kommer forhåpentligvis til å få samme svar som i a.

Oppgave 7

a)

100 m gjerde:

$100=2y+4x+2\cdot \sqrt{2}\cdot x$

Finner lengden av rektangelet, y, uttrykt ved x:

$y=50-2x-\sqrt{x}$

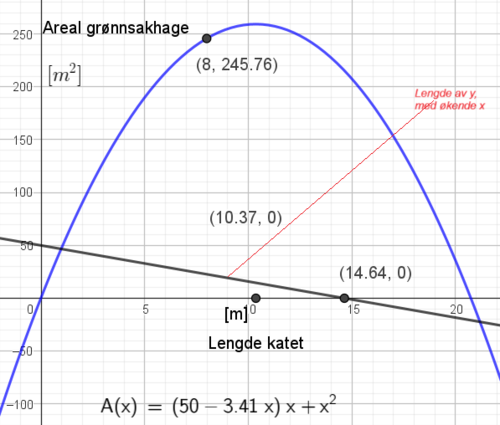
Arealet av grønnsakhagen blir:

$A(x)=y\cdot x+x^2=(50-2x-\sqrt{x})x+x^2$

Når katetet er 8 meter er arealet 245,76 kvadratmeter (linje 2).

b)

Fra figuren i a ser vi at dersom katetet har en lengde på 10 meter vil arealet være i nærheten av sin maksimale verdi (259 kvadratmeter).

c)