Løsning del 2 utrinn Vår 14

Oppgave 1

a)

$125\mathrm{kr}+105\mathrm{kr}+105=335\mathrm{kr}$

b)

Pris 25 enkeltbilletter:$25\cdot 125\mathrm{kr}=3125\mathrm{kr}$

Pris 1 klippekort à 25 klipp: $2665\mathrm{kr}$

Prisforskjell: $3125\mathrm{kr}-2665\mathrm{kr}=460\mathrm{kr}$

Anne sparer $\frac{460\mathrm{kr}}{3125\mathrm{kr}}=0,147=14,7\mathrm{\%}$

c)

Sum betalt: $2060\mathrm{kr}+910\mathrm{kr}+12\cdot 105\mathrm{kr}=4230\mathrm{kr}$

Gjennomsnitt per svømmetur: $\frac{4230\mathrm{kr}}{25+10+12}=\frac{4230\mathrm{kr}}{47}=90\mathrm{kr}/\mathrm{tur}$

Oppgave 2

a)

Til første bane kan vi velge blant 8 svømmere (8 muligheter). Til andre bane kan vi velge blant 7, osv helt til vi har igjen 1 svømmer som plasseres i den siste banen. Totalt antall kombinasjoner blir da $8\cdot 7\cdot 6\cdot 5\cdot 4\cdot 3\cdot 2\cdot 1=40320$.

b)

Eva svømmer med gjennomsnittsfarten $v=\frac{100\mathrm{m}}{100\mathrm{s}}=1\mathrm{m}/\mathrm{s}$. Etter $80\mathrm{s}$ er Anne i mål. Da har Eva bare svømt strekningen $s=1\mathrm{m}/\mathrm{s}\cdot 80\mathrm{s}=80\mathrm{m}$ (mens Anne har svømt de 100 metrene til mål). Eva vinner altså med $20\mathrm{m}$.

(I denne oppgaven må vi forutsette at de svømmer med konstant fart lik gjennomsnittsfarten.)

Oppgave 3

a), b)

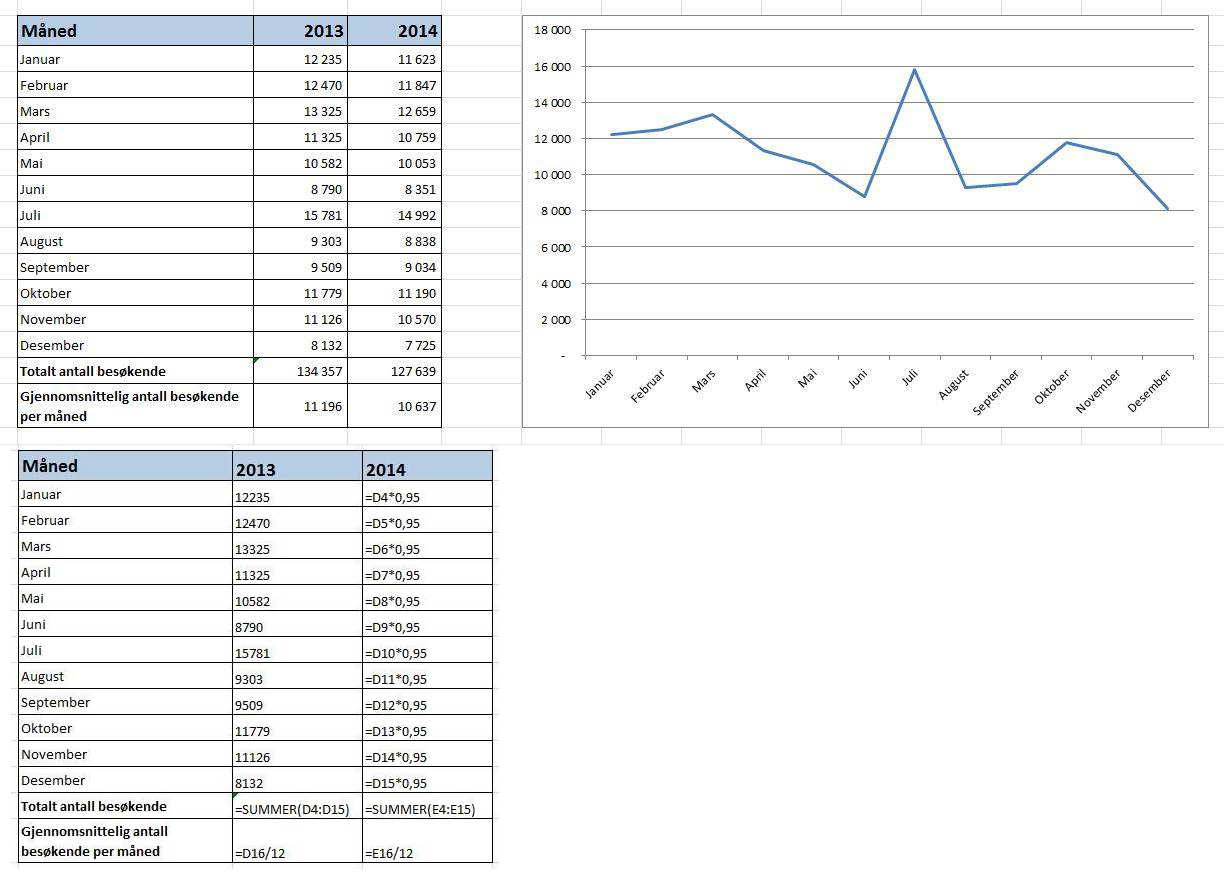
Se utklipp fra Excell under;

Oppgave 4

a)

Tegn et rektangel der lengden/den lengste siden er 10 cm og bredden/den korteste siden er 5 cm.

b)

Hele bassengets lengde er 25 m. Det betyr avstanden fra A til B horisontalt er $25\mathrm{m}-12,5\mathrm{m}-6,25\mathrm{m}=6,25\mathrm{m}.$. Høydeforskjellen mellom AB blir på tilsvarende måte $3,5\mathrm{m}-1,2\mathrm{m}=2,3\mathrm{m}$. Da gir Pytagoras' setning skråplanets lengde AB:

$(AB{)}^2=(6,25\mathrm{m}{)}^2+(2,3\mathrm{m}{)}^2$

$AB=\sqrt{44,35{\mathrm{m}}^2}$

$AB=6,66\mathrm{m}$

c)

Se for deg en vegg rett opp gjennom AD og en tilsvarende vegg ved BC. Kall bassenget/volumet lengst til venstre $V(1)$, det i midten $V(2)$ og det lengst til høyre $V(3)$. Regn ut disse volumene hver for seg, og summer dem til slutt:

$V(1)=6,25\mathrm{m}\cdot 12,5\mathrm{m}\cdot 3,5\mathrm{m}=273,44{\mathrm{m}}^3$

$V(2)=6,25\mathrm{m}\cdot 12,5\mathrm{m}\cdot 3,5\mathrm{m}-\frac{1}{2}\cdot 6,25\mathrm{m}\cdot 12,5\mathrm{m}\cdot 2,3\mathrm{m}=183,59{\mathrm{m}}^3$

$V(3)=12,5\mathrm{m}\cdot 12,5\mathrm{m}\cdot 1,2\mathrm{m}=187,50{\mathrm{m}}^3$

$V_{totalt}=V(1)+V(2)+V(3)=273,44{\mathrm{m}}^3+183,59{\mathrm{m}}^3+87,50{\mathrm{m}}^3=644,5{\mathrm{m}}^3$

d)

Etter en time (60 min) har det blitt tappet ut

$300\mathrm{L}/\min \cdot 60\min =18000\mathrm{L}=18{\mathrm{m}}^3$ vann. Dette er mindre enn volumet av det øverste sjiktet med vann (mindre enn volumet av vannet over skråplanet). Vi kan dermed sette opp likningen

$18{\mathrm{m}}^3=25\mathrm{m}\cdot 12,5\mathrm{m}\cdot h$

$h=\frac{18}{25\cdot 12,5}\mathrm{m}=0,058\mathrm{m}$,

Vannstanden har altså sunket 5,8 cm ned etter én time.

Oppgave 5

a)

Vi får et konstantledd på $+645000$ da dette er volumet vann ved start ($x=0$). Dessuten får vi et negativt førstegradsledd, $-1800x$. Dette skyldes at volumet minker med 18000 liter hver time.

b)

Tomt for vann når $V(x)=0$. Det gir:

$0=-18000x+645000$

$18000x=645000$

$x=\frac{645000}{18000}\mathrm{h}=35,83\mathrm{h}=35\mathrm{h}$ $50\min$

c)

Bruker Geogebra (Versjon 4.2). I inntastingsfeltet (nederst) bruker vi kommandoen:

"Funksjon[ <Funksjon>, <Start>, <Slutt> ]"

Helt konkret taster vi inn:

"Funksjon[-18000x + 645000, 0, 36]"

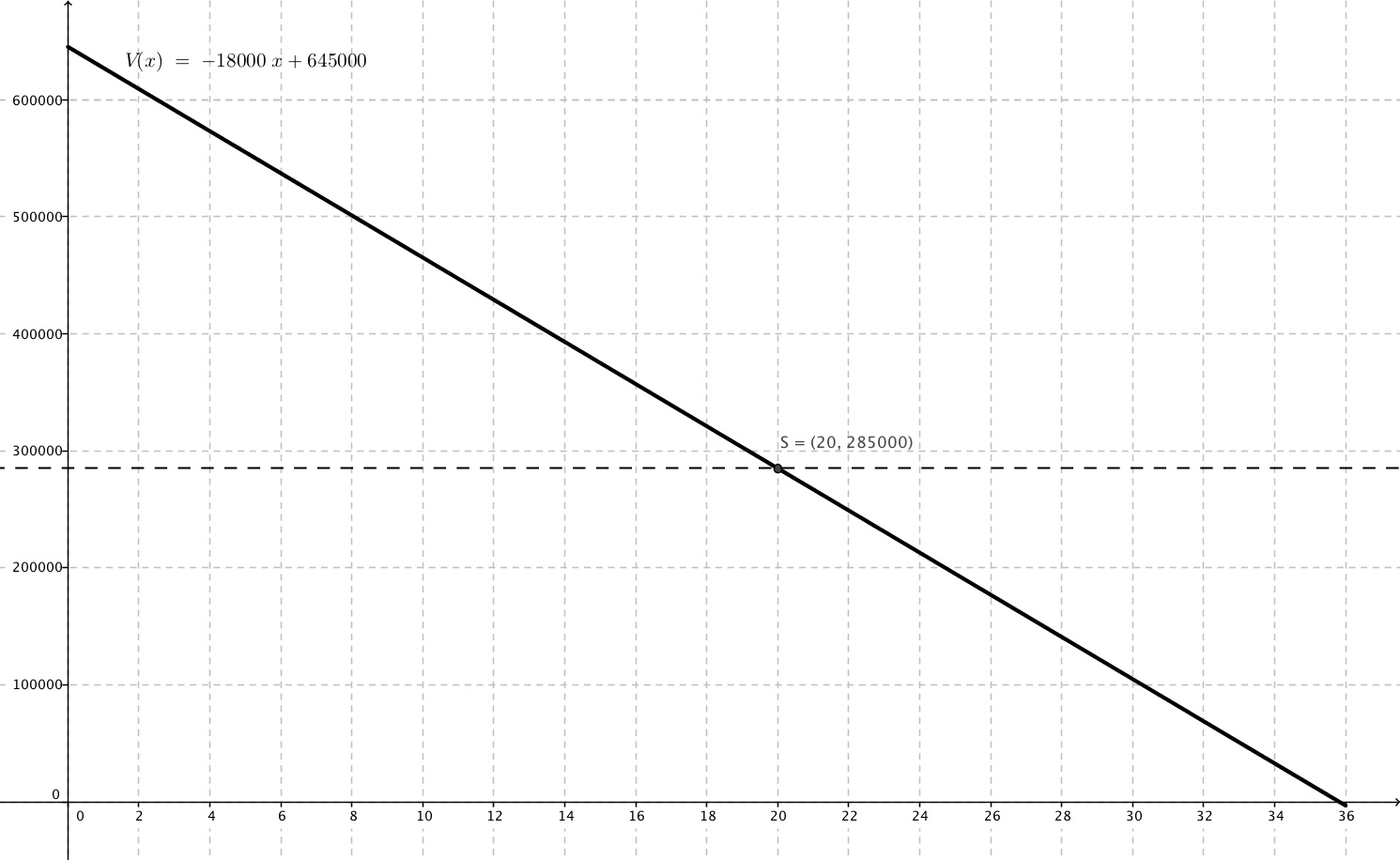
Funksjonen blir da hetende f. Høyreklikker på funksjonen i algebrafeltet og gir den nytt navn; V. Grafen blir seende ut som på figuren i deloppgave d) under.

d)

I inntsatingsfeltet skriver vi "y=285000". Deretter finner vi skjæring mellom de to linjene. Bruker da verktøyet "Skjæring mellom to objekt" fra menylinjen, og klikker deretter på de to linjene. Vi får skjæringspunktet $S$ med $x$-koordinat 20, se figur under. Det tar altså 20 timer før bassengets volum er 285 000 liter.

$x$-aksen er tiden målt i timer. $y$-aksen antall liter i bassenget.