S1 2014 vår LØSNING
Løsningsforslag som pdf laget av mattepratbruker Christianac
Diskusjon av denne oppgaven på matteprat
Del 1
Oppgave 1
a)
\begin{align*} -x^2+3x-3&=3-2x\\ -x^2+5x-6&=0 \end{align*} Bruker ABC-formelen: \begin{equation} x=\frac{-b \pm \sqrt{b^2-4ac}}{2a} \notag \end{equation} ABC-formelen gir $\underline{\underline{x=2 \lor x=3}}$
b)
\begin{align*} \lg(x+2) &= 2 \lg x \\ \lg(x+2) &= \lg x^2\\ 10^{\lg (x+2)} &= 10^{\lg x^2} \\ x+2 &= x^2\\ -x^2 + x +2 &= 0 \end{align*} ABC-formelen gir $x=2 \lor x=-1$, men $x=-1$ er ingen gyldig løsning siden man kun kan ta logaritmen til positive tall. $\underline{\underline{x=2}}$
Oppgave 2
\begin{align*} &\quad\;2 \cdot \lg \Big ( \frac{a^2}{b^2} \Big ) + 3 \cdot \lg \Big ( \frac{b^2}{a} \Big ) + \lg \Big ( \frac{b}{a} \Big ) \\ &= 2( \lg a^2 - \lg b^2) + 3 ( \lg b^2 - \lg a ) + \lg b - \lg a \\ &= 4 \lg a - 4 \lg b + 6 \lg b - 3 \lg a + \lg b - \lg a \\ &= \underline{\underline{3 \lg b}}\\ \end{align*}
Oppgave 3
a)
\begin{align*} &\quad\; 2(a+b)^2 -2(a-b)^2 \\ &= 2(a^2 + 2ab + b^2) -2(a^2-2ab + b^2)\\ &=4ab + 4ab \\ &=\underline{\underline{8ab}} \end{align*}
b)
\begin{align*} &\quad\;\frac{a^{-4}\cdot b^2 \cdot a^3}{(a^2\cdot b)^{-3} \cdot a^0} \\\\ &=\frac{a^{-1}\cdot b^2}{a^{-6}\cdot b^{-3} \cdot 1}\\\\ &= a^{6-1} \cdot b^{2+3}\\ &=\underline{\underline{(ab)^5}} \end{align*}
Oppgave 4
\begin{equation} \notag f(x)=\frac{ax+b}{x-1} \quad , \quad D_f=\mathbb{R} \backslash \{ 1 \}\\ \end{equation}
a)
Får oppgitt at funksjonen skjærer y-aksen i $y=6 \implies x=0 \land y=6$ \begin{align*} f(x)&=\frac{ax+b}{x-1}\\ 6&=\frac{a\cdot 0+b}{0-1}\\ 6&=\frac{b}{-1}\\ b&=\underline{\underline{-6}} \end{align*}
Får videre oppgitt at funksjonen skjærer x-aksen i $x=3 \implies x=3 \land y=0$ \begin{align*} f(x)&=\frac{ax+b}{x-1}\\ 0&=\frac{3a+b}{3-1}\\ 0&=\frac{3x-6}{2}\\ 3&=\frac{3x}{2}\\ x&=\underline{\underline{2}} \end{align*}
c)
Oppgave 5
a)
Et tall inne i Pascals trekant er alltid summen av de to tallene som står ovenfor. Dette gir følgende likningssett: \begin{align*} x + y &= 28\\ y + 35 &= 8x \end{align*} Løser likningssettet ved å bruke innsettingsmetoden: \begin{align*} y&= 28 - x \\ (28 - x) + 35 &= 8x\\ 63 &= 9x\\ x &= \underline{\underline{7}} \\\\ y &= 28 - 7 \\ y &= \underline{\underline{21}} \end{align*}
b)
Observerer mønsteret:
\begin{align*} (a+b)^4 &= 1\cdot a^4 + 4\cdot a^3b + 6 \cdot a^2b^2 + 4 \cdot a b^3 + 1\cdot b^4 \\ (a+b)^5 &= \underline{\underline{1\cdot a^5 + 5 \cdot a^4b + 10 \cdot a^3b^2 + 10 \cdot a^2 b^3 + 5 \cdot a b^4 + 1 \cdot b^5 }} \end{align*}
c)
Skal fylle ut tabellen med sannsynligheten for $A$ inntreffer $k$ ganger. Sannsynligheten for at $A$ inntreffer i hvert delforsøk er $a$. Sannsynligheten for at vi får $a$ tre ganger på rad i tre delforsøk er dermed $a^3$.
På hvilke måter kan $A$ inntreffe i 2 av 3 delforsøk? Vi kan ha:
$(A,A,\bar{A}),(A,\bar{A},A)$ eller $(\bar{A}, A, A)$ med sannsynligheter $(aab),(aba)$ og $(baa)$. Summen av disse sannsynlighetene blir da: $a^2b + a^2b + a^2b = \underline{3a^2b}$. På denne måten kan vi fylle ut det resterende av tabellen.
| k | 3 | 2 | 1 | 0 |
| P(X=k) | $a^3$ | $3a^2b$ | $3ab^2$ | $b^3$ |
Oppgave 6
a)
\begin{align*} O(x)&=I(x)-K(x)\\ O(x)&=p\cdot x -(0.1x^2 -10x + 20000)\\ O(x)&=-0.1x^2+10x + px - 20000\\ O(x)&=\underline{\underline{-0.1x^2+x(10+p)-20000}} \end{align*}
b)
\begin{align*} O(x)&=-0.1x^2+150x-20000 \end{align*}
Har et uttrykk på formen $ax^2+bx+c$. Hvis $a<0$ kan vi være sikre på at grafen til funksjonen har et toppunkt og ikke et bunnpunkt. Dermed kan vi trygt derivere og sette den deriverte lik null. Vi vil da finne produksjonsmengden som gir størst overskudd.
\begin{align*} O'(x)&=-0.2x+150\\ 0&=-0.2x+150\\ 0.2x&=150\\ x&=\underline{\underline{750}} \end{align*}
Med $p=140$ vil det gi størst overskudd å produsere $750$ enheter.
c)
Det er oppgitt at overskuddet er størst når bedriften produserer og selger 2000 enheter. Vi kan dermed anta at $O'(x)=0 \land x=2000$. \begin{align*} O'(x)&= -0.2x+(10+p)\\ 0 &= -0.2 \cdot 2000 + 10 + p \\ 0 &= -400 + 10 + p \\ p &= \underline{\underline{390}} \end{align*}
Oppgave 7
Har at definisjonen av den deriverte er: \begin{equation} f'(x)=\lim_{h \to 0} \frac{f(x+h) -f(x)}{h} \notag \end{equation} Vi har allerede fått oppgitt at $f(x)=x^2+2x$ så det eneste vi trenger å finne er $f(x+h)$. \begin{align*} f(x+h)&=(x+h)^2 + 2(x+h) \\ f(x+h)&=x^2 + 2xh + h^2 +2x +2h \end{align*} Setter så inn i definisjonen til den deriverte: \begin{align*} f'(x)&=\lim_{h \to 0} \frac{f(x+h) -f(x)}{h} \\ f'(x)&=\lim_{h \to 0} \frac{x^2 + 2xh + h^2 +2x +2h -(x^2 +2x)}{h}\\ f'(x)&=\lim_{h \to 0} \frac{2xh + h^2 +2h}{h}\\ f'(x)&=\lim_{h \to 0} \frac{\cancel{h}(2x + h +2)}{\cancel{h}}\\ f'(x)&=\lim_{h \to 0} 2x+2 +h\\ f'(x)&=\underline{\underline{2x+2}} \end{align*}
Del 2
Oppgave 1)
a)
$120m^2$ totalt og $20m^2$ er vindu. Da må $100m^2$ være isolert veggflate.Definerer varmetapet, V, til å være \begin{align*} V=0.009x + 0.048y \end{align*}
Setter inn i likingen for $V$ og får: \begin{align*} V=0.009\frac{kWh}{m^2} \cdot 100m^2 + 0.048\frac{kWh}{m^2} \cdot 20m^2 \end{align*} Løser denne på kalkulator: \begin{align*} V=1.86 kWh \end{align*} For å få varmetap per time deler vi da på antall timer $(h)$ og får svaret $\underline{\underline{1.86kW}}$
b)
\begin{align*} x+y &= 120\\ 0.009 \cdot x + 0.048 \cdot y &= 2 \end{align*} Løser også denne på kalkulator og får \begin{align*} x &\approx 96.4 \\ y &\approx 23.6\\ \end{align*} For at det totale varmetapet skal være $2kWh$ må arkitekten velge $96.4m^2$ med isolert veggflate og $23.6m^2$ med vindu.
Oppgave 2
\begin{align*} f(x)=x^4-8x^2+16 \quad, D_f =\mathbb{R} \end{align*}
a)
Skjærer y-aksen når $x=0$ \begin{align*} f(0)=0^4-8\cdot 0^2 +16 f(0)=16 \end{align*} $\underline{\underline{f(x) \text{skjærer y-aksen i} (0,16)}}$.
b)
Faktoriserer uttrykket ved hjelp av 2. og 3. kvadratsetning. \begin{align*} f(x)&=x^4-8x^2+16\\ f(x)&=(x^2-4)^2\\ f(x)&=((x+2)(x-2))^2\\ \end{align*} Ser at $f(x)=0$ hvis en av faktorene $(x+2)$ eller $(x-2)$ er lik null. Dermed har $f(x)$ nullpunkter for $x=2\lor x=-2$.
c)
\begin{align*} f'(x)&=4x^3-16x\\ f'(x)&=4x(x^2-4)\\ f'(x)&=4x(x+2)(x-2)\\ \end{align*} $f(x)$ har topp- og bunnpunkter når $f'(x)=0$, dermed \begin{align*} 4x(x+2)(x-2)=0 \end{align*} $f'(x)=0$ når $x=0 \lor x=2 \lor x=-2 $. Her bør det tegnes fortegnsskjema for å finne ut hva som er topp- og hva som er bunnpunkter! Ender opp med at $f(x)$ har bunnpunkt i $(2,0),(-2,0)$ og toppunkt i $(0,16)$.
Oppgave 3
a)
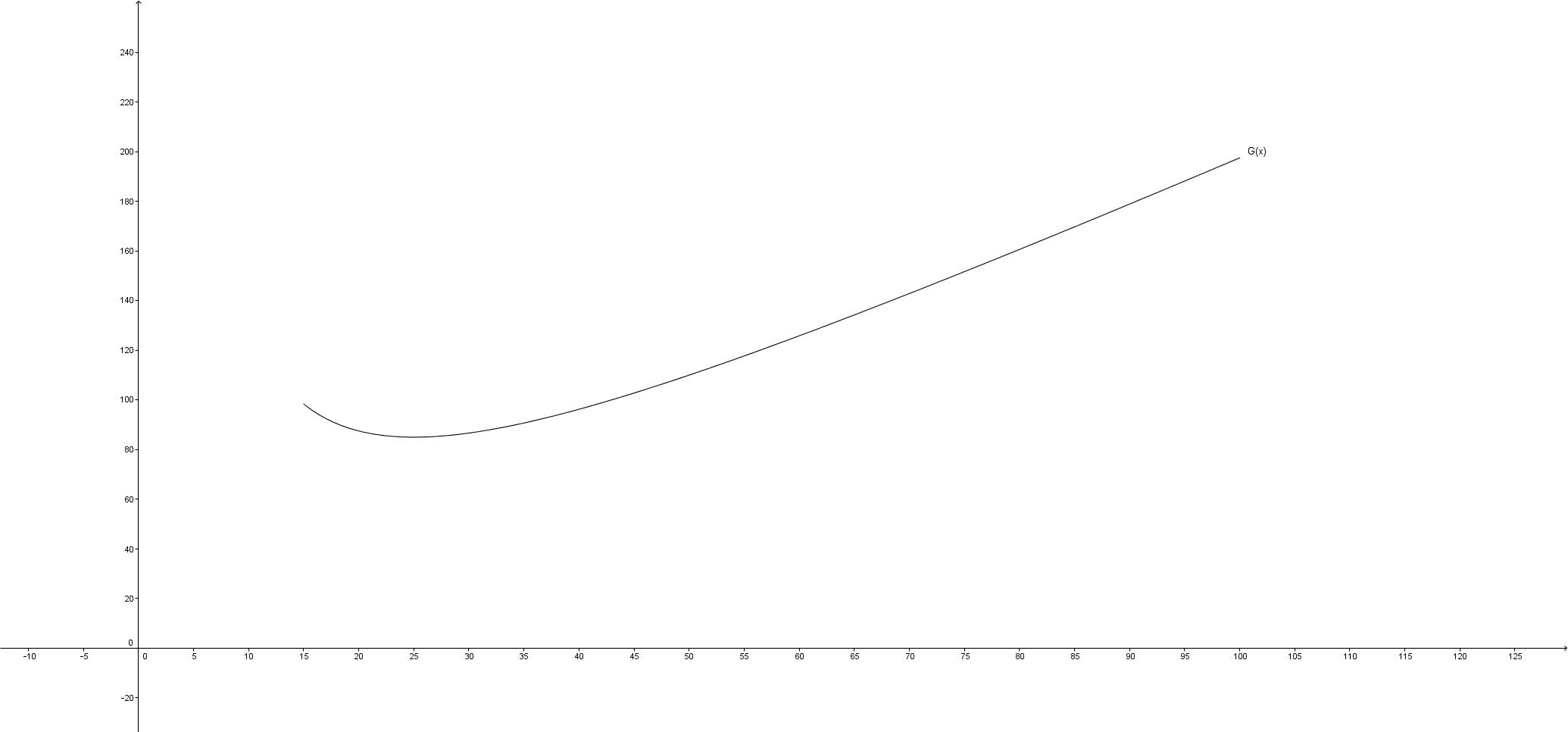
Har at Arealet til området er \begin{align*} A=x\cdot y \end{align*} Videre kan vi skrive lengden av gjerdet som omkretsen av området minus 15 meter som består av steinmur \begin{align*} G(x)&=2y + x + (x-15)\\ G(x)&=2y + 2x -15\\ \end{align*} Vi får oppgitt at arealet av området er lik $625m^2$. Setter inn for dette og løser med hensyn på y. \begin{align*} 625=x\cdot y\\ y=\frac{625}{x} \end{align*} Denne kan vi igjen sette inn i uttrykket for $G(x)$ som vil gi oss svaret vi ønsker: \begin{align*} G(x)&=2\Big ( \frac{625}{x} \Big ) +2x -15\\ G(x)&=\underline{\underline{ \frac{1250}{x} + 2x -15}}\\ \end{align*}
b)
c)
Ser at grafen til funksjonen kun har ett bunnpunkt i det aktuelle intervallet $<15,\infty>$. Vi kan derfor trygt derivere $G(x)$ for å finne det korteste gjerdet bonden kan bruke. \begin{align*} G'(x)&=-\frac{1250}{x^2}+2\\ G'(x)&=-\frac{1250}{x^2} + \frac{2x^2}{x^2}\\ G'(x)&=\frac{2x^2-1250}{x^2}\\ G'(x)&=\frac{2(x+25))(x-25)}{x^2} = 0 \end{align*} Siden det er forutsatt at $x>15$ er eneste løsning at bondens korteste gjerde er 25 meter. Å bruke et negativt antall meter med gjerde gir heller ingen mening. \begin{align*} x&=25\\ y&=\frac{625}{25}\\ y&=25 \end{align*} Kan da regne ut lengden av gjerdet som \begin{align*} G(25)&=\frac{1250}{25}+2\cdot 25 -15 \\ G(25)&=85 \end{align*} Ser at begge sidene er like lange, altså har rektangelet blitt til et kvadrat og gjerdet er 85 meter langt.
Oppgave 4
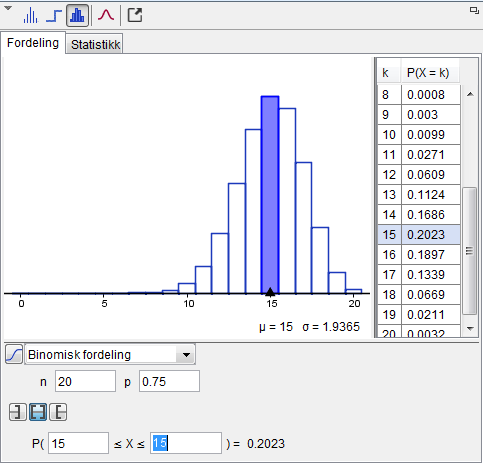
I denne oppgaven er det en stor fordel å bruke sannsynlighetskalkulatoren i Geogebra.\\ Vi har et utvalg på $20 \Leftrightarrow n = 20$\\ Sannsynligheten for suksess i forsøkene er $\frac{3}{4} \Leftrightarrow p = 0.75$\\
a)
$P(X=15)=P(15 \leq X \leq 15) = \underline{\underline{0.2023}}$
b)
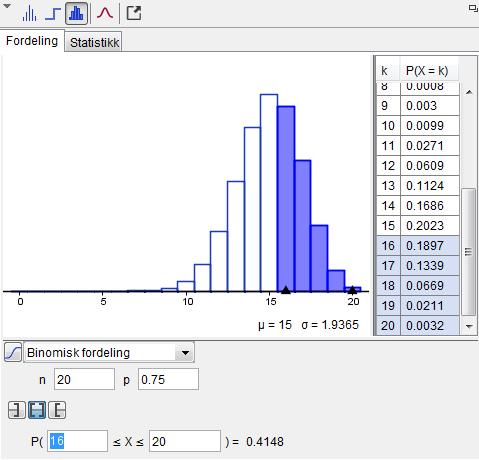 $P(X>15)=P(16 \leq X \leq 20) = \underline{\underline{0.4148}}$
$P(X>15)=P(16 \leq X \leq 20) = \underline{\underline{0.4148}}$
c)
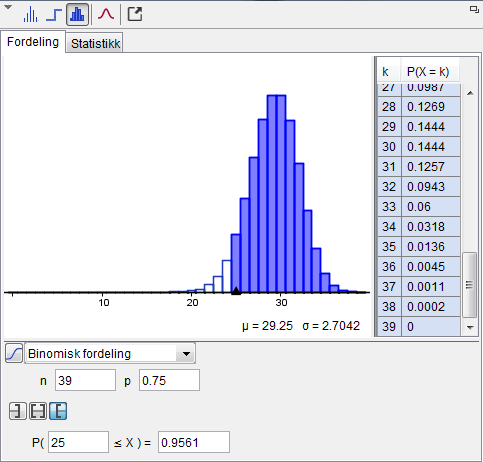
Her er det enkleste å prøve seg frem i kalkulatoren til du finner et utvalg som er stort nok til at det er $95\%$ sannsynlighet for at minst 25 arbeider som lærer. Dette er en løsningsmetode som vil gi full uttelling i følge sensorveiledningen.
Vi ser at $n=39$ det minste utvalget som oppfyller kriteriene i oppgaven.
Oppgave 5
a)
Deriverer for å finne toppunkt. Har også her at $(a<0)$. \begin{align*} F'(x)&=-0.02x+0.3 = 0\\ x&=15 \end{align*} Fortjenesten per enhet blir størst mulig dersom bedriften produserer 15 enheter.\\\\
b)
$F(x)$ er profitten per enhet. Dersom man multipliserer profitten per enhet med antall solgte enheter får du bedriftens totale profitt, altså overskuddet. \\
c)
\begin{align*} O(x)&=x\cdot F(x)\\ O(x)&=x(-0.01x^2+0.3x+120)\\ O(x)&=-0.01x^3+0.3x^2+120x\\\\ O'(x)&= -0.03x^2+0.6x+120 = 0 \end{align*}
$$x\approx -54 \lor x \approx 74$$
\begin{align*} O(74)&= 6471 \end{align*} Bedriften kan ikke produsere et negativt antall enheter, dermed oppnår bedriften størst overskudd ved å produsere 74 enheter. Overskuddet er da på 6471 kroner.\\
Oppgave 6
a)
\begin{align*} 0.35x + 0.20y &\leq 250\\ 0.15x + 0.40y &\leq 300\\ x+y &\leq 900\\ x &\geq 0 \\ y &\geq 0 \\ \end{align*}
b)
c)
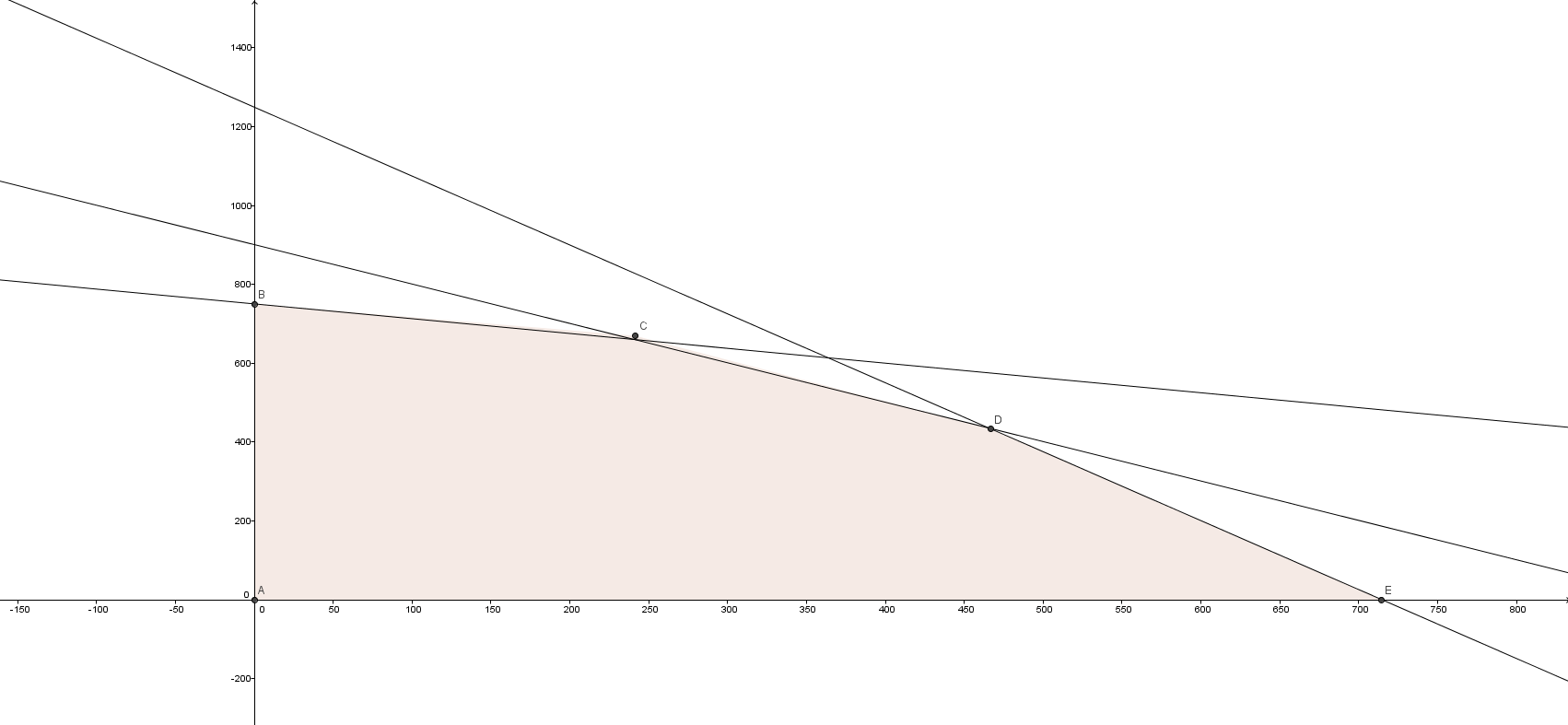
Lager en fortjenestefunksjon, $f$, og bruker en glider i Geogebra for å se hvor nivålinja tangerer det mulige produksjonsområdet.
\begin{align*} f=8x+12y \end{align*} Denne tangerer området i punktet $C(240,660)$, Altså bør hun produsere 240kg saft og 660kg syltetøy. \begin{align*} f&=8\cdot 240 + 12 \cdot 660\\ f&=9840 \end{align*} Fortjenesten hennes blir da 9840 kroner. \newpage
Oppgave 7
a)
\begin{align*} n^n \cdot \Big ( \frac{x}{n} \Big )^{\lg x} &= x^n\\ \Big ( \frac{x}{n} \Big )^{\lg x} &= \frac{x^n}{n^n}\\ \Big ( \frac{x}{n} \Big )^{\lg x} &= \Big (\frac{x}{n} \Big )^n\\ \lg \Big ( \frac{x}{n} \Big )^{\lg x} &= \lg \Big (\frac{x}{n} \Big )^n\\ \end{align*}
b)
\begin{align*} \lg \Big ( \frac{x}{n} \Big )^{\lg x} &= \lg \Big (\frac{x}{n} \Big )^n\\ \lg x^{\lg x} -\lg n^{\lg x}&= n \lg x - n\lg n\\ \lg x (\lg x - \lg n ) &= n(\lg x - \lg n)\\ \lg x (\lg x - \lg n) -n(\lg x - lg n) &= 0 \end{align*}
Trekker ut $(\lg x -\lg n)$ som felles faktor.
\begin{align*} (\lg x - n)(\lg x - \lg n) = 0 \end{align*}
c)
Likningen er kun oppfylt dersom én av faktorene er lik null. Dette gir:
\begin{align*} \lg x - n &= 0\\ \lg x &= n\\ x &= \underline{\underline{10^n}} \end{align*} eller \begin{align*} \lg x - \lg n &= 0\\ \lg x &= \lg n \\ x &= \underline{\underline{n}} \end{align*}