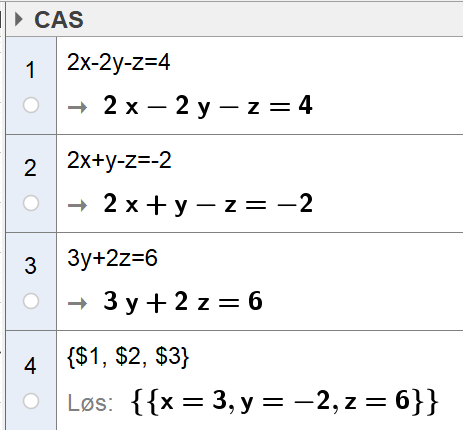R2 2019 høst LØSNING

oppgaven som pdf

Diskusjon av denne eksamensoppgaven

Løsningsforslag til del 1 laget av Emilga

Løsningsforslag til del 2 laget av Kristian Saug

Løsningsforslag laget av Ole Henrik Morgenstierne

Løsning til del 1 som videoer laget av Lektor Håkon Raustøl

Løsning til del 2 som videoer laget av Lektor Håkon Raustøl

DEL 1

Oppgave 1

a)

$f(x)=2cos(\pi x)$

$f^{\prime }(x)=-2\pi sin(\pi x)$

b)

$g(x)=co{s}^{2}x\cdot sinx$

$$\begin{gathered} g^{\prime }(x)=(co{s}^{2}x{)}^{\prime }\cdot sinx+co{s}^{2}x\cdot (sinx{)}^{\prime } \\ =2cosx\cdot (-sinx)\cdot sinx+co{s}^{2}x\cdot cosx \\ =-2si{n}^{2}x\cdot cosx+co{s}^{3}x \end{gathered}$$

Oppgave 2

a)

$$\begin{gathered} {\int }_{-1}^1(2x^3+3x-1)dx \\ =[\frac{2}{4}{x}^4+\frac{3}{2}{x}^2-x{]}_{-1}^1 \\ =(\frac{1}{2}\cdot 1^4+\frac{3}{2}\cdot 1^2-1)-(\frac{1}{2}\cdot (-1{)}^4+\frac{3}{2}\cdot (-1{)}^2-(-1)) \\ =(\frac{1}{2}+\frac{3}{2}-1)-(\frac{1}{2}+\frac{3}{2}+1) \\ =-1-1=-2 \end{gathered}$$

b)

$u=2x^2-1$

$\frac{du}{dx}=4x\Rightarrow dx=\frac{du}{4x}$

$$\begin{gathered} \int \frac{8x}{\sqrt{2x^2-1}}dx=\int \frac{8x}{\sqrt{u}}\cdot \frac{du}{4x}=\int \frac{2}{\sqrt{u}}du=2\int u^{-\frac{1}{2}}du \\ =\frac{2}{\frac{1}{2}}\cdot u^{\frac{1}{2}}+C=4\cdot \sqrt{u}+C=4\sqrt{2x^2-1}+C \end{gathered}$$

c)

$\int \frac{2}{(x+3)(x+1)}dx=\int \frac{A}{(x+3)}+\frac{B}{(x+1)}dx$

Vi bestemmer A og B ved å løse likningen:

$$\begin{gathered} 2=(x+1)A+(x+3)B \\ 2=Ax+A+Bx+3B \\ 2=(A+B)x+A+3B \end{gathered}$$

Telleren har ikke noe x-ledd, så vi har:

I $A+B=0$

II$A+3B=2$

Setter inn $A=-B$ i likning II:

$-B+3B=2\Rightarrow B=1$

Fra likning I har vi da $A=-1$

Integralet blir da:

$$\begin{gathered} \int \frac{2}{(x+3)(x+1)}dx=\int \frac{A}{(x+3)}+\frac{B}{(x+1)}dx=\int \frac{-1}{(x+3)}+\frac{1}{(x+1)}dx \\ =-\ln |x+3|+\ln |x+1|+C=\ln |\frac{x+1}{x+3}|+C \end{gathered}$$

Oppgave 3

a)

Summen av en aritmetisk rekke er gitt ved

$S_n=\frac{n\cdot (a_1+a_n)}{2}$

Vi må finne antall ledd i rekken $7+11+....+479+483$.

Ser at $d=4$, så antall ledd (n) blir:

$n=\frac{483-7}{4}+1=\frac{476}{4}+1=119+1=120$

Summen av denne rekken blir:

$S_{120}=\frac{120\cdot (7+483)}{2}=60\cdot (7+483)=420+28980=29400$

b)

For en geometrisk rekke har vi

$a_n=a_1\cdot k^{n-1}$

Vi vet at $a_2=6$ og får likning I:

$$\begin{gathered} a_2=a_1\cdot k^{2-1} \\ 6=a_1\cdot k \\ {a}_1=\frac{6}{k} \end{gathered}$$

Summen av en geometrisk rekke som konvergerer er gitt ved

$S=\frac{a_1}{(1-k)}$

Vi vet at summen av rekken er 24 og har dermed likning II:

$$\begin{gathered} 24=\frac{a_1}{(1-k)} \\ {a}_1=24(1-k) \end{gathered}$$

Setter inn $a_1=\frac{6}{k}$ i likning II:

$$\begin{gathered} \frac{6}{k}=24(1-k) \\ 6=24k(1-k) \\ 6=24k-24k^2 \\ 24k^2-24k+6=0 \\ {k}^2-k+\frac{1}{4}=0 \\ (k-\frac{1}{2})(k-\frac{1}{2})=0 \\ k=\frac{1}{2} \end{gathered}$$

Setter inn $k=\frac{1}{2}$ i likning I:

$a_1=\frac{6}{\frac{1}{2}}=12$

Oppgave 4

a)

$2sin(2x)=1$, der $x\in [0,\pi ]$

$sin(2x)=\frac{1}{2}$

$2x=\frac{\pi }{6}+k\cdot 2\pi \vee 2x=(\pi -\frac{\pi }{6})+k\cdot 2\pi k\in \mathbb{Z}$

$x=\frac{\pi }{12}\vee x=\frac{5\pi }{12}$ kun disse to løsningene gir $x\in [0,\pi ]$

$L=\{\frac{\pi }{12},\frac{5\pi }{12}\}$

b)

$2co{s}^{2}x-cosx=1$, der $x\in [0,4\pi ]$

$u=cosx$

$$\begin{gathered} 2u^2-u-1=0 \\ {u}^2-\frac{1}{2}u-\frac{1}{2}=0 \\ (u+\frac{1}{2})(u-1)=0 \\ u=-\frac{1}{2}\vee u=1 \\ cosx=-\frac{1}{2}\vee cosx=1 \end{gathered}$$

$cosx=-\frac{1}{2}\Rightarrow x=\frac{2\pi }{3}+k\cdot 2\pi \Rightarrow L=\{\frac{2\pi }{3},\frac{8\pi }{3}\}$ for $x\in [0,4\pi ]$

og $cosx=-\frac{1}{2}\Rightarrow x=\frac{4\pi }{3}+k\cdot 2\pi \Rightarrow L=\{\frac{4\pi }{3},\frac{10\pi }{3}\}$ for $x\in [0,4\pi ]$

$cosx=1\Rightarrow x=0+k\cdot 2\pi \Rightarrow L=\{0,2\pi ,4\pi \}$ for $x\in [0,4\pi ]$

$L=\{0,\frac{2\pi }{3},\frac{4\pi }{3},2\pi ,\frac{8\pi }{3},\frac{10\pi }{3},4\pi \}$

Oppgave 5

B er grafen til f.

Dette fordi $si{n}^2(x)=0$ for $x=0,x=\pi$ og $x=2\pi$ i intervallet $x\in [0,2\pi ]$. Dette er de samme nullpunktene som for $sin(x)$.

I tillegg er $si{n}^2(x)=1$ for $x=\frac{\pi }{2}$ og $x=\frac{3\pi }{2}$ i intervallet $x\in [0,2\pi ]$

Oppgave 6

a)

$f(x)=x+a,0\le x\le 2,a>0$

${\int }_0^{2}f(x)dx=3$

$[\frac{1}{2}{x}^2+ax{]}_0^2=3$

$(\frac{1}{2}\cdot 2^2+a\cdot 2)-(\frac{1}{2}\cdot 0^2+a\cdot 0)=3$

$\frac{4}{2}+2a-0=3$

$2a=3-2$

$a=\frac{1}{2}$

b)

$V={\int }_0^2\pi (f(x){)}^{2}dx$

$=\pi {\int }_0^2(x+a{)}^{2}dx$

$=\pi {\int }_0^2(x^2+2ax+a^2)dx$

$=\pi [\frac{1}{3}{x}^3+\frac{2a}{2}{x}^2+a^{2}x{]}_0^2$

$=\pi [(\frac{1}{3}\cdot (2{)}^3+a\cdot (2{)}^2+a^2\cdot 2)-(\frac{1}{3}\cdot (0{)}^3+a\cdot (0{)}^2+a^2\cdot 0)]$

$=\pi (\frac{8}{3}+4a+2a^2)$

Setter inn uttrykket for V i likningen:

$V=\frac{98}{3}\pi$

$\pi (\frac{8}{3}+4a+2a^2)=\frac{98}{3}\pi |:\pi$

$\frac{8}{3}+\frac{3\cdot 4a}{3}+\frac{3\cdot 2a^2}{3}=\frac{98}{3}$

$\frac{8}{3}+\frac{12a}{3}+\frac{6a^2}{3}=\frac{98}{3}|\cdot 3$

$6a^2+12a+8-98=0$

$6a^2+12a-90=0|:6$

$a^2+2a-15=0$

$(a+5)(a-3)=0$

$a=-5\vee a=3$

Forkaster $a=-5$ siden vi må ha $a>0$. Vi har da $a=3$.

Oppgave 7

a)

I xz-planet er $y=0$. Setter inn $y=0$ i uttrykket for $y$:

$$\begin{gathered} y=2-t \\ 0=2-t \\ t=2 \end{gathered}$$

Setter inn $t=2$ i uttrykket for $x$:

$$\begin{gathered} x=1+2t \\ x=1+2\cdot 2 \\ x=5 \end{gathered}$$

Setter inn $t=2$ i uttrykket for $z$:

$$\begin{gathered} z=6+t \\ z=6+2 \\ z=8 \end{gathered}$$

Skjæringspunktet mellom linjen $\ell$ og xz-planet er (5,0,8).

b)

Linjen $\ell$ står vinkelrett på planet $\alpha$, og retningsvektoren til linjen $\ell$ er derfor lik normalvektoren $\overrightarrow{n_{\alpha }}$ til planet $\alpha$. Dermed er skalarproduktet av $\overrightarrow{n_{\alpha }}$ og en vektor i planet, lik 0.

Likningen for planet er derfor gitt ved:

$[a,b,c]\cdot [x-x_0,y-y_0,z-z_0]=0$

$a(x-x_0)+b(y-y_0)+c(z-z_0)=0$

Der a,b og c er koordinatene til planets normalvektor, og $x_0,y_0,z_0$ er et punkt i planet. Vi har $\overrightarrow{n_{\alpha }}=[2,-1,1]$ og punktet $P(2,-2,6)$.

$$\begin{gathered} 2(x-2)-1\cdot (y-(-2))+1\cdot (z-6)=0 \\ 2x-4-(y+2)+z-6=0 \\ 2x-y+z-4-2-6=0 \\ 2x-y+z-12=0 \end{gathered}$$

Likningen for planet $\alpha$ er $2x-y+z-12=0$.

c)

Setter inn uttrykkene for x,y og z fra parameterfremstillingen til linjen $\ell$, i likningen for planet $\alpha$:

$$\begin{gathered} 2x-y+z-12=0 \\ 2\cdot (1+2t)-(2-t)+(6+t)-12=0 \\ 2+4t-2+t+6+t-12=0 \\ 6t-6=0 \\ t=1 \end{gathered}$$

Setter inn $t=1$ i uttrykkene for x,y og z fra parameterfremstillingen til linjen $\ell$:

$x=1+2t=1+2\cdot 1=3$

$y=2-t=2-1=1$

$z=6+t=6+1=7$

Skjæringspunktet mellom $\alpha$ og $\ell$ er (3,1,7).

Oppgave 8

Vi har gitt differensiallikningen:

$y^{\prime }-2y=x,y(0)=1$

a)

Integrerende faktor er $e^{-2x}$

$y^{\prime }-2y=x$

$e^{-2x}{y}^{\prime }-2e^{-2x}y=x{e}^{-2x}$

$(e^{-2x}y{)}^{\prime }=x{e}^{-2x}$

$y{e}^{-2x}=\int x{e}^{-2x}dx$

Bruker delvis integrasjon, der $u=x$, $u^{\prime }=1$, $v^{\prime }=e^{-2x}$, $v=-\frac{1}{2}{e}^{-2x}$

$y{e}^{-2x}=x\cdot (-\frac{1}{2}{e}^{-2x})-\int (-\frac{1}{2}{e}^{-2x})dx$

$y{e}^{-2x}=-\frac{1}{2}x{e}^{-2x}-(-\frac{1}{2})\cdot (-\frac{1}{2})\cdot e^{-2x}+C$

$y(x)=-\frac{1}{2}x-\frac{1}{4}+C{e}^{2x}$

Vi har $y(0)=1$

$-\frac{1}{2}\cdot 0-\frac{1}{4}+C{e}^{2\cdot 0}=1$

$0-\frac{1}{4}+C\cdot 1=1$

$C=1+\frac{1}{4}$

$C=\frac{5}{4}$

Setter inn verdien for C i likningen for y:

$y(x)=-\frac{1}{2}x-\frac{1}{4}+\frac{5}{4}{e}^{2x}$

b)

Finner stigningstallet til tangenten til y i punktet (0,1):

$$\begin{gathered} y^{\prime }=x+2y \\ {y}^{\prime }=0+2\cdot 1 \\ {y}^{\prime }=2 \end{gathered}$$

Finner likningen for tangenten til y i punktet (0,1):

$$\begin{gathered} (y-y_1)=a(x-x_1) \\ (y-1)=2(x-0) \\ y=2x+1 \end{gathered}$$

Oppgave 9

Finner lengden av vektorene mellom sentrum av sirklene:

$\overrightarrow{AB}=[1-1,2-(-1),4-0]=[0,3,4]$

$|\overrightarrow{AB}|=\sqrt{0^2+3^2+4^2}=\sqrt{25}=5$

$\overrightarrow{BC}=[5-1,1-2,-4-4]=[4,-1,-8]$

$|\overrightarrow{BC}|=\sqrt{4^2+(-1{)}^2+(-8{)}^2}=\sqrt{81}=9$

$\overrightarrow{AC}=[5-1,1-(-1),-4-0]=[4,2,-4]$

$|\overrightarrow{AC}|=\sqrt{4^2+2^2+(-4{)}^2}=\sqrt{36}=6$

Finner radien $a,b$ og $c$ til hver av kulene:

$$\begin{gathered} Ia+b=5 \\ IIb+c=9 \\ IIIa+c=6 \end{gathered}$$

$$\begin{gathered} Ia=5-b \\ IIc=9-b \\ III5-b+9-b=6 \\ -2b=6-5-9 \\ b=\frac{-8}{-2}=4 \end{gathered}$$

$$\begin{gathered} Ia=5-4=1 \\ IIc=9-4=5 \end{gathered}$$

Radien til kulen med sentrum i A er 1, radien til kulen med sentrum i B er 4, radien til kulen med sentrum i C er 5.

Oppgave 10

Vi skal vise at $n^3-n$ er delelig med 3 for alle $n\in \text{N}$

1. Induksjonsgrunnlag: $n=1$ gir $1^3-1=0$, som er delelig med 3.

2. Induksjonstrinnet: Vi antar at $n^3-n$ er delelig delelig med 3 når $n=k$. Med $n=k+1$ får vi:

$$\begin{gathered} (k+1{)}^3-(k+1) \\ =(k+1)((k+1{)}^2-1) \\ =(k+1)((k^2+2k+1)-1) \\ =(k+1)(k^2+2k) \\ =k^3+2k^2+k^2+2k \\ =k^3+3k^2+2k \\ =k^3+3k^2+2k+k-k \\ =k^3-k+3k^2+3k \\ =(k^3-k)+3(k^2+k) \end{gathered}$$

$k^3-k$ er delelig med 3, ifølge antakelsen for $n=k$. $3(k^2+k)$ er en faktor av 3, og er derfor delelig med 3. Summen av to ledd som begge er delelig med 3, er også delelig med 3. Vi har vist at $n^3-n$ er delelig med 3 for $n=k+1$.

$n^3-n$ er delelig med 3 for alle $n\in \text{N}$, hvilket skulle vises.

DEL 2

Oppgave 1

a)

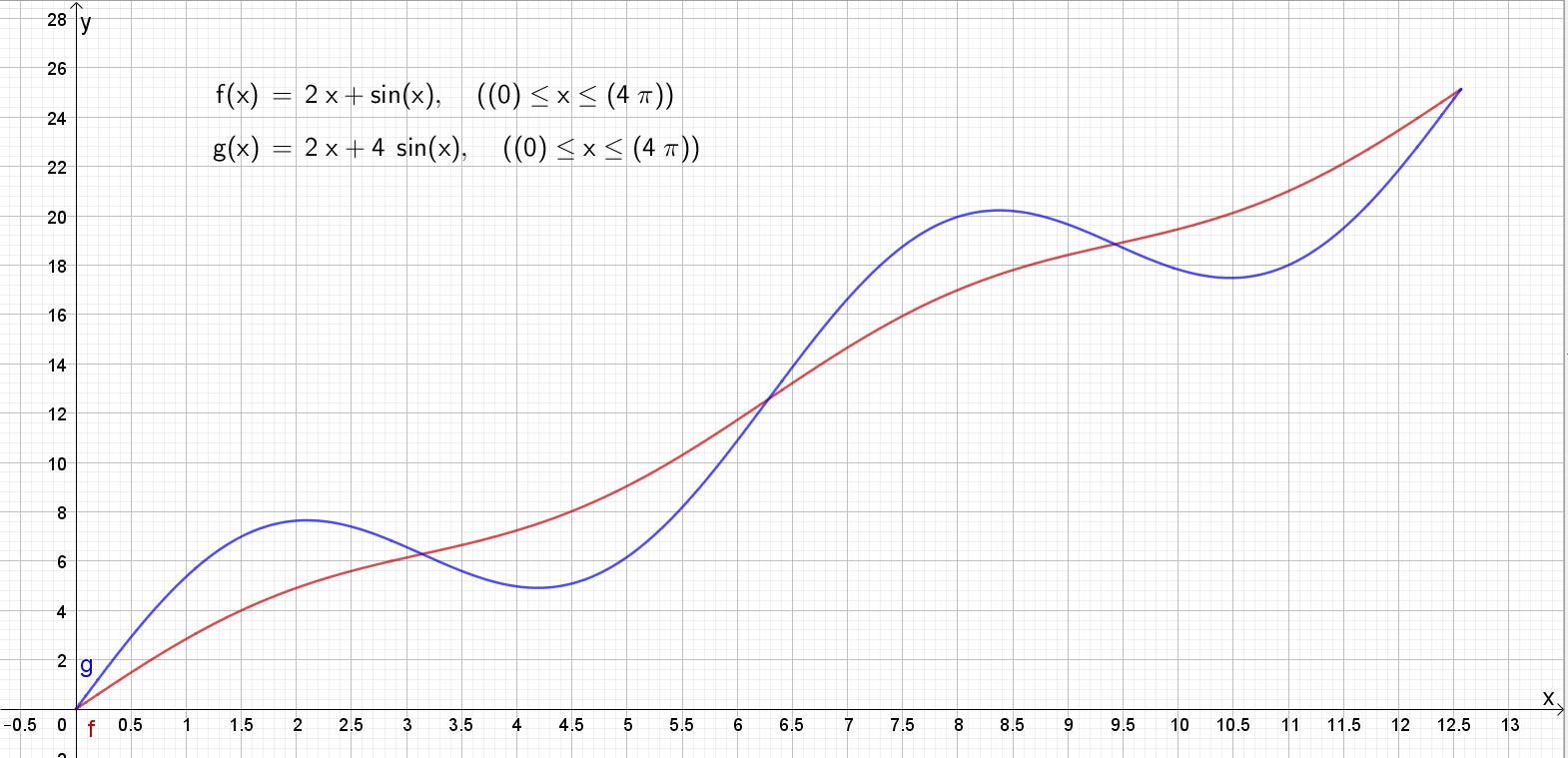
Bruker Geogebra til å tegne grafene til f og g i samme koordinatsystem.

b)

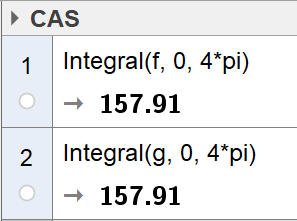
Bruker CAS i Geogebra til å bestemme arealet under grafen til f og arealet under grafen til g.

Arealet under grafen til f er 157,91 og arealet under grafen til g er også 157,91.

c)

Bruker CAS i Geogebra til å finne volumet til hvert av de to omdreiingslegemene.

Volumet til omdreiingslegemet til f er 8174,07.

Volumet til omdreiingslegemet til g er 7996,42.

d)

Bruker CAS i Geogebra til å vise at arealet til F er uavhengig av k.

Vi ser i linje 6 at arealet ikke er avhengig av k, hvilket skulle vises. $16{\pi }^2$ er for øvrig samme verdi som vi fikk i a).

e)

Bruker CAS til å bestemme hvilken verdi for k som gir minst volum til omdreiingslegemet.

$k=4$ gir minst volum.

Oppgave 2

a)

Bruker CAS i Geogebra til å finne skjæringspunktet til de tre planene.

Planene skjærer hverandre i punktet P(3,-2,6).

b)

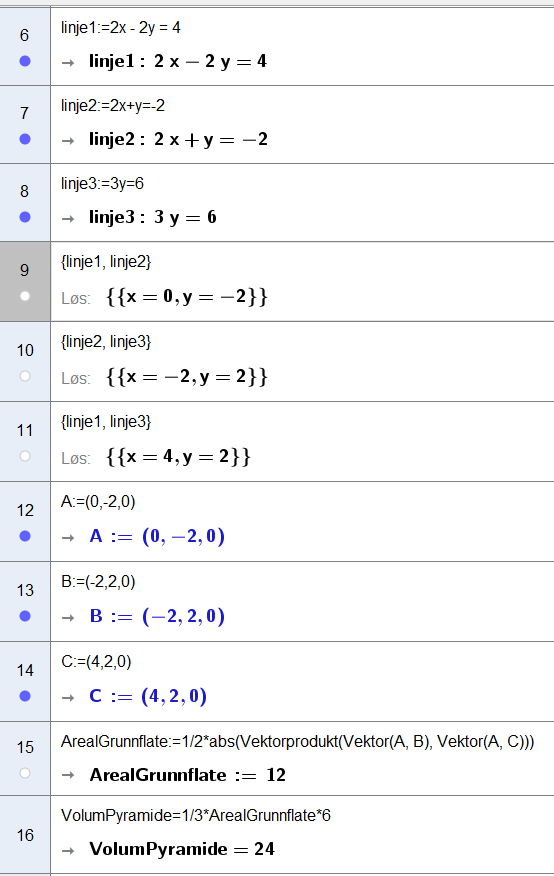
Bruker CAS i Geogebra til å finne volumet av pyramiden.

Linje 6,7,8 i CAS: z-verdien er 0 i xy-planet. Definerer de tre linjene som avgrenser grunnflaten til pyramiden.

Linje 9,10,11 i CAS: finner hjørnene til grunnflaten i pyramiden, i xy-planet.

Linje 12,13,14 i CAS: uttrykker hjørnene til grunnflaten som punkter i rommet, punkt A, B og C.

Linje 15 i CAS: Finner arealet av grunnflaten til pyramiden, ved å ta halvparten av absoluttverdien kryssproduktet til vektor AB og AC (siden kryssproduktet spenner ut et parallellogram, og arealet av en trekant er halvparten av arealet til et parallellogram).

Linje 16 i CAS: Finner volumet av pyramiden med formelen $V=\frac{1}{3}\cdot G\cdot h$. Høyden h er 6, siden z-verdien til punkt P er 6.

Volumet av pyramiden er 24.

Oppgave 3

a)

Bruker CAS i Geogebra.

Vi har vist at Sveins samlede inntekt i årene 2020–2029 da vil bli i overkant av 5,97 millioner kroner.