1P 2021 høst K06 LØSNING

Oppgave 1

Det betyr at 5 elever utgjør 20%, Da er 25 elever 100%.

Oppgave 2

I perioden har hun hatt en lønnsøkning på 12%. KPI var 12,2%, altså har hun hatt en nedgang i kjøpekraft.

Oppgave 3

Målestokk 5 : 1 er en forstørrelse av virkeligheten. Delen skal være $\frac{5}{1}=\frac{140}{x}$. Dvs. x = 28 mm lang.

Oppgave 4

Påstand 1 er riktig: $prisperelev=\frac{totalutgift}{Antallelever}$

Påstand 2 er feil: $x$ og $x^2$ er eksempler på størrelser der dersom x øker så øker kvadratet av x også, men de er ikke propirsjonale.

Påstand 3 er riktig: $y=\frac{k}{x}$, om vi dobler x : $y=\frac{k}{2x}$, halveres y.

Påstand 4 er feil: Forholdet mellom areal og omkrets vil være: $\frac{A}{O}=\frac{\pi r^2}{s\pi r}=\frac{r}{2}$. Dette forholdet er ikke konstant, men varierer med r. Derfor ikke proporsjonalitet.

Oppgave 5

Ja, vinduets diagonal er 20 dm (pytagoras), så det er mulig dersom platen ikke er for tykk.

Oppgave 6

a)

Sidekant kube:

$s^3=64$

$s=4$

b)

Volum av det rektangulære prismet.:

$x\cdot 4x\cdot 4=64$

$16x^2=64$

$x=2$

Bredden av grunnflaten er 2 cm, lengden er 8 cm, og høyden 4 cm.

Oppgave 7

a)

f(x) vi ser at grafen krysser y aksen i 3 og at stigningstallet er -2 (to til høyre og fire ned). Det gir f(x) = -2x + 3

g(x) = 1/2 x - 2 ( stigningstall: to til høyre og en opp (delta y delt på delta x)

b)

Høyden i trekanten er 1. Grunnlinjen er : g(x)=0 gir x = 4, og f(x)= 0 gir x = 1,5. Grunnlinjen G= 4 - 1,5 = 2,5. Arealet blir halvparten av G*h som er 1,25.

Oppgave 8

a)

Sannsynligheten for 10 i ett kast er 1/12. I to kast: $P(10og10)=\frac{1}{12}\cdot \frac{1}{12}=\frac{1}{144}$

b)

Det stemmer, hun kan få 10 og 12 eller 12 og 10: $P(10,12)=\frac{1}{144}+\frac{1}{144}=\frac{1}{72}$

c)

Det er 144 mulige utfall. Utfallene som gir 20 eller mer er vist her:

Gunstige delt på mulige gir 15/144, eller 10,4%

Oppgave 1

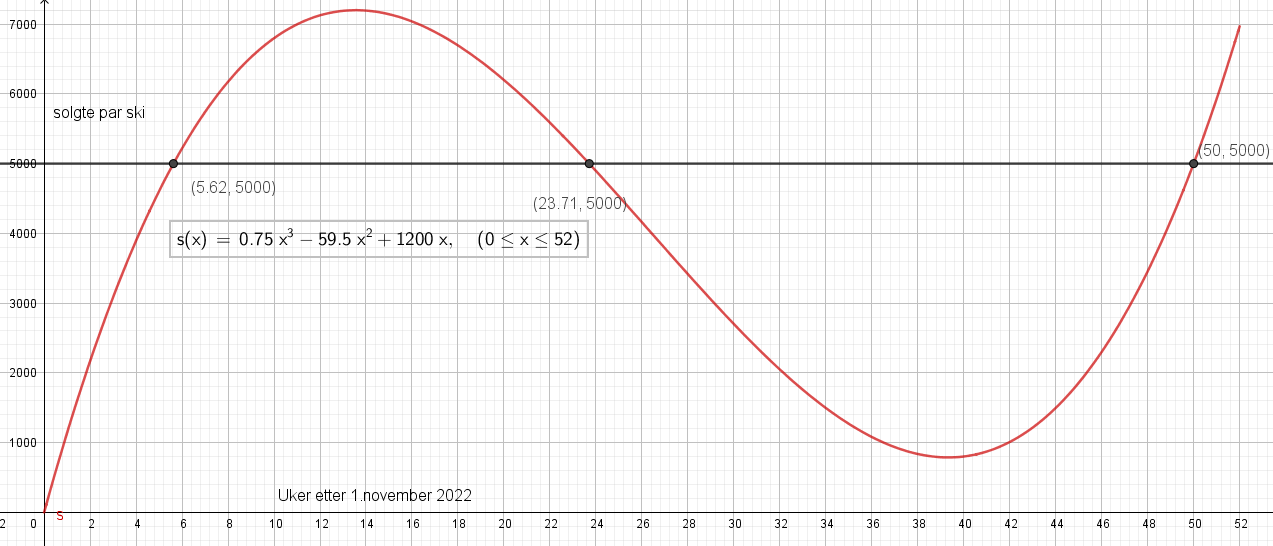
a)

b)

I ca. 18 + 2 uker ,altså 20 uker. Se figur i a.

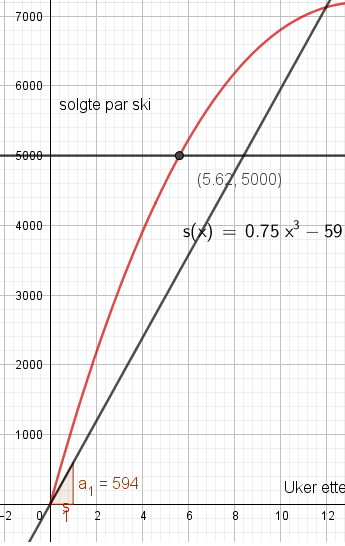
c)

Stigningstallet, 594, viser den gjennomsnittlige veksten i salget de 12 første ukene etter oppstart.

Oppgave 2

$reallønn=\frac{nominell\cdot 100}{KPI}$

$nominell=\frac{reallønncdotKPI}{100}=\frac{499109\cdot 112,2}{100}=560000$

Da må man ha en lønn på 560 tusen kroner.

Oppgave 3

a)

Boksen er 5 cm bredere fra toppen. Fra siden danner sidekanten på 13 cm, høyden og "overhenget på 5 cm en rettvinklet trekant.

$h=\sqrt{{13}^2-5^2}=12$ cm

b)

Volum boks:

$V=20cm\cdot 12cmcdot8cm=1920c{m}^3$, eller 1,92 liter.

c)

Overflate boks:

O = bunn + 2 kortsider + 2 langsider = $8cm\cdot 15cm+2\cdot 8cm\cdot 13cm+2\cdot 12cm\cdot 20cm=808c{m}^2$

Det er den ytre overflaten av boksen uten lokk.

Oppgave 4

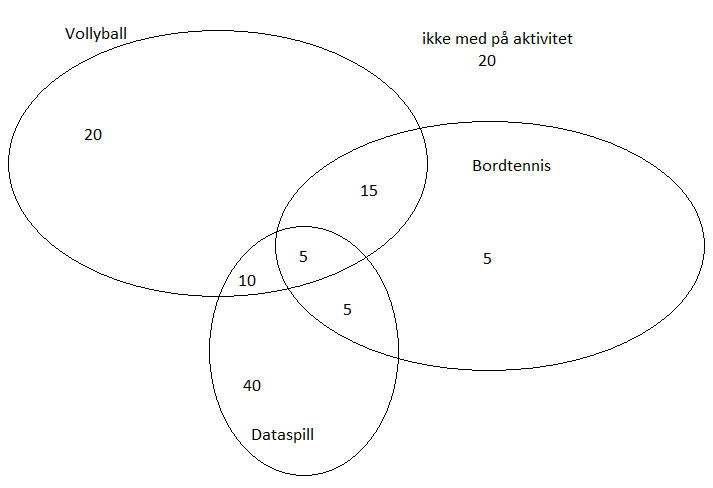
a)

b)

P(deltar ikke) = 20/120 = 1/6 = 16,67%