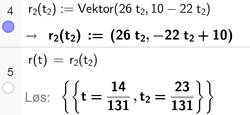R1 2022 Vår LK20 LØSNING

Oppgaven som pdf

Diskusjon av oppgaven på matteprat

Videoløsning del 1 av Lektor Lainz

Løsning som pdf av Farhan Omar

DEL 1

Oppgave 1

a)

$f(x)=x^3+lnx$

$f^{\prime }(x)=3x^2+\frac{1}{x}$

b)

$g(x)=x\cdot e^{2x}$

$g^{\prime }(x)=1\cdot e^{2x}+x\cdot 2\cdot e^{2x}=e^{2x}(1+2x)$

Oppgave 2

$e^{2x}-e^x=2$

$(e^x{)}^2-e^x-2=0$

Setter $u=e^x$

$u^2-u-2=0$

$(u+1)(u-2)=0$

$u=-1\vee u=2$

$e^x=-1\vee e^x=2$

Forkaster det negative svaret fordi ln(-1) ikke er definert.

$ln(e^x)=ln(2)$

$x=ln(2)$

Oppgave 3

$\underset{x\to 3}{lim}\frac{x-3}{x^2+x-12}$

$=\underset{x\to 3}{lim}\frac{x-3}{(x-3)(x+4)}$

$=\underset{x\to 3}{lim}\frac{1}{x+4}$

$=\frac{1}{7}$

Oppgave 4

a)

$\overrightarrow{AC}=[t-1,4-2]=[t-1,2]$

$\overrightarrow{AB}=[-1-1,5-2]=[-2,3]$

Dersom vinkelen mellom to vektorer er 90 grader, er skalarproduktet av disse to vektorene lik 0.

$\overrightarrow{AC}\cdot \overrightarrow{AB}=0$

$[t-1,2]\cdot [-2,3]=0$

$(t-1)\cdot (-2)+2\cdot 3=0$

$-2t+2+6=0$

$-2t=-8$

$t=4$

Anbefaler å tegne punktene i et koordinatsystem for å se at det stemmer.

b)

Dersom A, B og C skal ligge på en rett linje, er $\overrightarrow{AC}$ og $\overrightarrow{AB}$ parallelle. Da har vi at:

$\overrightarrow{AC}=k\cdot \overrightarrow{AB}$

$[t-1,2]=k\cdot [-2,3]$

Dette gir oss to likninger:

$It-1=-2k$

$II2=3k\Rightarrow k=\frac{2}{3}$

Setter inn k=2/3 inn i likning I:

$It-1=-2\cdot \frac{2}{3}$

$t=\frac{-4}{3}+1$

$t=-\frac{1}{3}$

Anbefaler å tegne punktene i et koordinatsystem for å se at det stemmer.

Oppgave 5

a)

Eleven ønsker å finne toppunktet til funksjonen f, i intervallet $x\in [0,\to ⟩$. (Er det flere enn ett toppunkt i dette intervallet, finner programmet kun det første toppunktet).

Linje 1-2: her defineres funksjonen f(x)

Linje 4: variabelen x gis verdien 0

Linje 5: variabelen h gis verdien 0,001

Linje 6: dette er en while-løkke som gjentar operasjonen i linje 7, så lenge funksjonsverdien f(x) er mindre enn eller lik funksjonsverdien f(x+h).

Linje 7 (inni while-løkka): verdien til x økes med h.

Linje 9: etter at while-løkken er ferdig, skrives verdien til x ut. Dette er en tilnærming til x-verdien hvor funksjonsverdien f(x) ikke lenger er mindre eller lik funksjonsverdien f(x+h). Vi har da funnet tilnærmet x-verdi for toppunktet til funksjonen.

b)

Vi kan finne toppunktet ved regning, ved å sette f'(x) lik 0.

$f(x)=\frac{x}{1+x^2}$

$f^{\prime }(x)=\frac{1\cdot (1+x^2)-x\cdot 2x}{(1+x^2{)}^2}=\frac{1+x^2-2x^2}{x^4+2x^2+1}=\frac{-x^2+1}{x^4+2x^2+1}$

Setter f'(x)=0:

$\frac{-x^2+1}{x^4+2x^2+1}=0$

$-x^2+1=0$

$x^2=1$

$x=-1\vee x=1$

Vi forkaster det negativet svaret, siden programmet bare finner toppunktet for $x\in [0,\to ⟩$

Sjekker at x=1 er et toppunkt, og ikke et bunnpunkt eller terrassepunkt, ved å sjekke at den deriverte er positiv før ekstremalpunktet (grafen til f vokser), og at den deriverte er negativ etter ekstremalpunktet (grafen til f synker):

$f^{\prime }(0)=\frac{-0^2+1}{0^4+2\cdot 0^2+1}=\frac{1}{1}=1$

$f^{\prime }(2)=\frac{-2^2+1}{2^4+2\cdot 2^2+1}=\frac{-4+1}{16+8+1}=\frac{-3}{25}$

Vi har nå vist at funksjonen har et toppunkt i x=1.

DEL 2

Oppgave 1

$f(x)=\{\begin{array}{lrr}{x}^2+1& ,& x<2\\ x-t& ,& x\ge 2\end{array}$

a)

For at funksjonen f skal være kontinuerlig, må grenseverdien når x går mot 2 fra venstre, være lik grenseverdien når x går mot 2 fra høyre.

$\underset{x\to 2^{-}}{lim}{x}^2+1=5$

$\underset{x\to 2^{+}}{lim}x-t=5\Rightarrow t=-3$

b)

Vi må sjekke om $\underset{x\to 2}{lim}{f}^{\prime }(x)$ eksisterer.

$f^{\prime }(x)=\{\begin{array}{lrr}2x& ,& x<2\\ 1& ,& x>2\end{array}$

$\underset{x\to 2^{-}}{lim}{f}^{\prime }(x)=\underset{x\to 2^{-}}{lim}2x=4$

$\underset{x\to 2^{+}}{lim}{f}^{\prime }(x)=\underset{x\to 2^{+}}{lim}1=1$

Grenseverdien eksisterer ikke, og $f^{\prime }(2)$ eksisterer derfor ikke. Funksjonen er ikke deriverbar i $x=2$, når $t=-3$.

Oppgave 2

a)

Vi har $\overrightarrow{u}=\overrightarrow{a}+\overrightarrow{b}$.

$|\overrightarrow{u}{|}^2={\overrightarrow{u}}^2=(\overrightarrow{a}+\overrightarrow{b}{)}^2={\overrightarrow{a}}^2+2\cdot \overrightarrow{a}\overrightarrow{b}\cdot {\overrightarrow{b}}^2$

$=|\overrightarrow{a}{|}^2+2\cdot \overrightarrow{a}\overrightarrow{b}\cdot |\overrightarrow{b}{|}^2=2^2+2\cdot (-3)+3^2=4-6+9=7$

$|\overrightarrow{u}|=\sqrt{7}\approx 2,6$

Vi har $\overrightarrow{v}=\overrightarrow{a}-6\overrightarrow{b}$.

$|\overrightarrow{v}{|}^2={\overrightarrow{v}}^2=(\overrightarrow{a}-6\overrightarrow{b}{)}^2={\overrightarrow{a}}^2-2\cdot \overrightarrow{a}\cdot 6\cdot \overrightarrow{b}+(-6\overrightarrow{b}{)}^2$

$=|\overrightarrow{a}{|}^2-12\cdot \overrightarrow{a}\cdot \overrightarrow{b}+36\cdot |\overrightarrow{b}{|}^2=2^2-12\cdot (-3)+36\cdot 3^2=4+36+36\cdot 9=364$

$|\overrightarrow{v}|=\sqrt{364}\approx 19,1$

b)

Finner skalarproduktet av $\overrightarrow{u}$ og $\overrightarrow{v}$:

$\overrightarrow{u}\cdot \overrightarrow{v}=(\overrightarrow{a}+\overrightarrow{b})\cdot (\overrightarrow{a}-6\overrightarrow{b})$

$={\overrightarrow{a}}^2-6\cdot \overrightarrow{a}\cdot \overrightarrow{b}+\overrightarrow{a}\cdot \overrightarrow{b}-6\cdot {\overrightarrow{b}}^2$

$={\overrightarrow{a}}^2-5\cdot \overrightarrow{a}\cdot \overrightarrow{b}-6\cdot {\overrightarrow{b}}^2$

$=|\overrightarrow{a}{|}^2-5\cdot \overrightarrow{a}\cdot \overrightarrow{b}-6\cdot |\overrightarrow{b}{|}^2$

$=2^2-5\cdot (-3)-6\cdot 3^2$

$=4+15-54$

$=-35$

Finner vinkelen mellom $\overrightarrow{u}$ og $\overrightarrow{v}$:

$cos\alpha =\frac{\overrightarrow{u}\cdot \overrightarrow{v}}{|\overrightarrow{u}|\cdot |\overrightarrow{v}|}$

$cos\alpha =\frac{-35}{\sqrt{7}\cdot \sqrt{364}}$

$\alpha \approx {134}^{\circ }$

Oppgave 4

Bruker CAS i Geogebra.

Det tar ca. 7,8 timer før temperaturen i kaffen er mindre enn 40 grader Celsius.

Oppgave 5

a)

Vi kan bruke Pytagorassetningen for å avgjøre om trekanten er rettvinklet.

- Ta inn koordinatene til punktene A, B og C

- Beregne $A{B}^2$, $B{C}^2$ og $A{C}^2$ ved hjelp av koordinatene (bruker pytagorassetningen)

- Sjekke om $A{B}^2=B{C}^2+A{C}^2$, eller $A{C}^2=B{C}^2+A{B}^2$, eller $B{C}^2=A{B}^2+A{C}^2$. I så fall er trekanten rettvinklet. Ellers er den ikke det.

b)

Oppgave 6

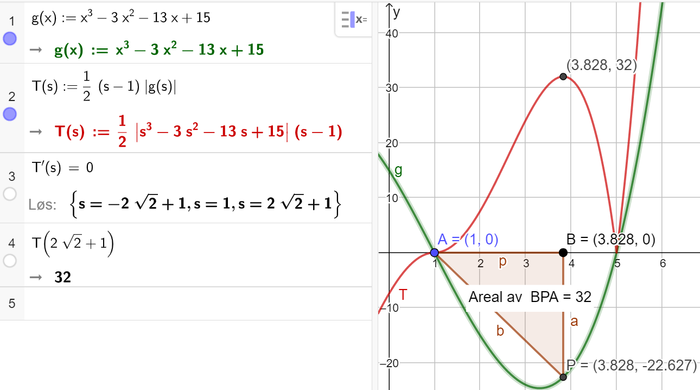
Løser oppgaven i CAS i Geogebra. Grafikkfeltet er med, fordi det kan være nyttig å tegne situasjonen i Geogebra, for å forstå oppgaven bedre.

Linje 1 i CAS: definerer funksjonen g(x)

Linje 2: Definerer funksjonen T for arealet av trekanten. Arealet av en trekant er 1/2*g*h. Her er grunnlinjen avstanden fra punkt A til punkt B, som er s-1. Høyden er avstanden fra punkt B til punkt P, som er absoluttverdien av g(s).

Linje 3: finner den s som gir størst areal til trekanten (finner s i ekstremalpunktene til T). Vi har at $s\in ⟨1,5⟩$, så det er kun $s=2\sqrt{2}+1$ som passer. Ser av grafen til T at vi har et toppunkt for denne verdien av s.

Linje 4: Den eksakte verdien av s som gir det største arealet til trekanten, er $s=2\sqrt{2}+1$. Arealet er da 32.

Oppgave 7

Løser oppgaven i CAS i Geogebra.

a)

Banefarten er ca. 31 km/t.

b)

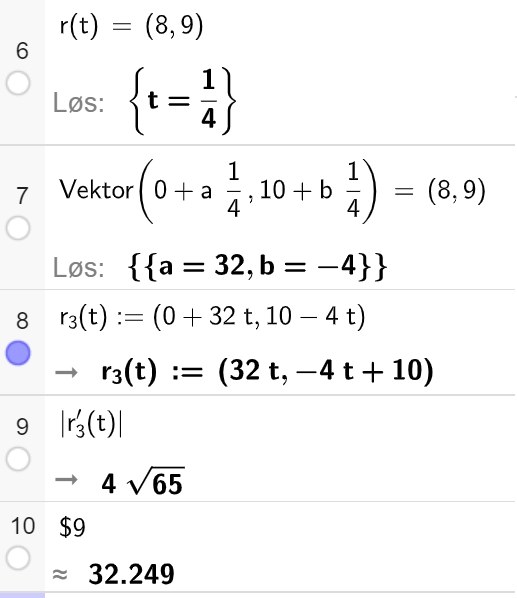
Undersøker for hvilken tid båtene har samme posisjon:

Politibåten og piratbåten er på samme sted til ulik tid. De møtes altså ikke.

c)