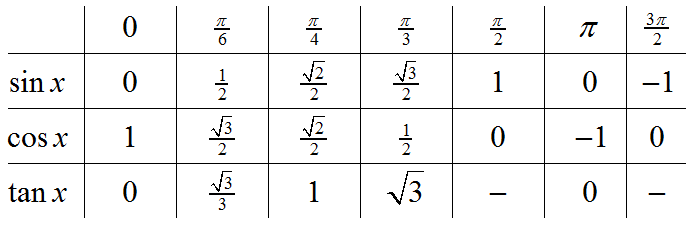Trigonometri R2

Absolutt vinkelmål

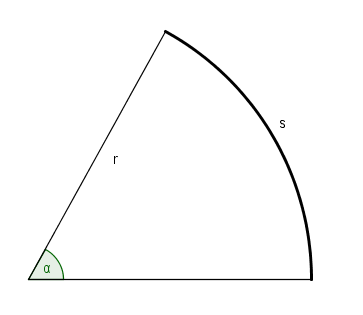
Radianer (også kalt absolutt vinkelmål) er definert som følger. Ta utgangspunkt i figuren:

Vi konstruerer en sirkelbue med lengde $s$ og radius $r$, som vist på figuren. Buen er avgrenset av de to radiene som går fra sentrum av buen. Vinkelen mellom de to radiene i radianer er da definert som

$\alpha =\frac{s}{r}$

Det følger at forholdet mellom radianer og grader er gitt ved

${360}^{\circ }=2\pi$

eller ekvivalent ved

$v{[}^{\circ }]=\frac{{180}^{\circ }}{\pi }v[\text{rad}]$ for en vinkel $v$

Trigonometeriske funksjoner

De tre sentrale trigonometriske funksjonene er sinus, cosinus og tangens, som er et produkt av sinus og cosinus. Sinus er den viktigste trigonometriske funksjonen, siden alle de andre trigonometriske funksjonene kan utledes fra denne.

Definisjon av sin x og cos x

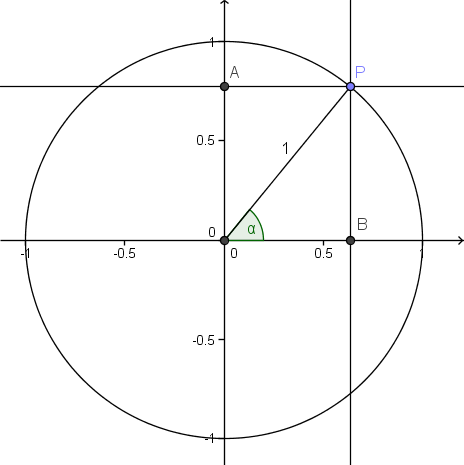
Ta utgangspunkt i figuren under:

Når vi konstruerer en enhetssirkel og en radius med vinkel $\alpha$ på x-aksen slik figuren viser, vil radien skjære sirkelperiferien i punktet $P$. Hvis trekker normalene fra $P$ på koordinataksene, vil de skjære disse i punktene $A$ og $B$ slik figuren viser. Da vil y-verdien til punktet $A$ være lik $\sin \alpha$ og x-verdien til punktet $B$ være lik $\cos \alpha$

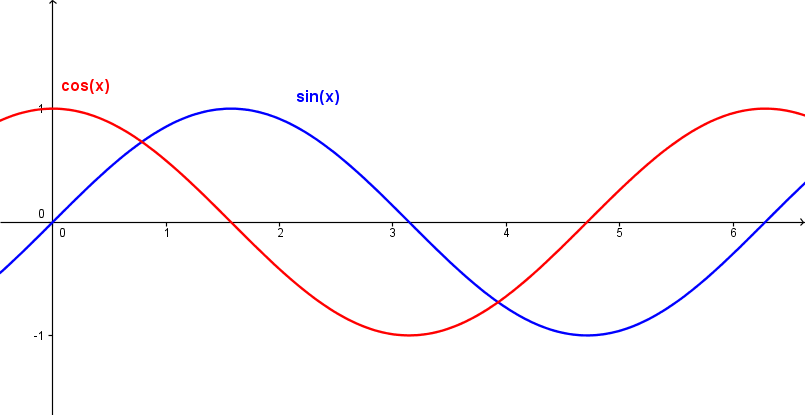
Når vi plotter sinus- og cosinuskurvene ser de slik ut:

Sinus- og cosinuskurvene har begge perioder på $2\pi$ radianer.

Merk at cosinusfunksjonen kun er sinusfunkjsonen forskjøvet $\frac{\pi }{2}$ radianer i minusretningen. Altså gjelder det at $sin(x+\frac{\pi }{2})=\cos x$

Definisjon av tan(x)

Tangensfunksjonen er definert slik at

$\tan x=\frac{\sin x}{\cos x}$

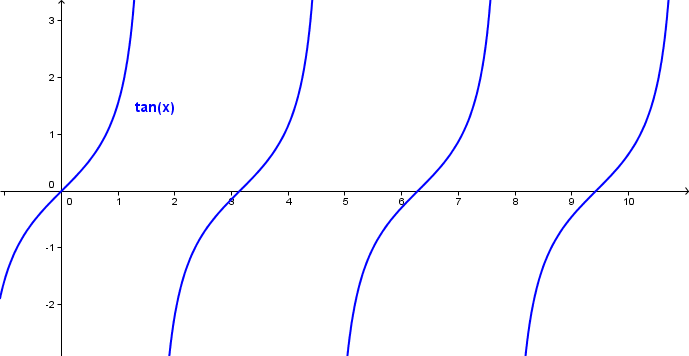
Når vi plotter tangenskurven, ser den slik ut:

Tangenskurven har en periode på $\pi$ radianer.

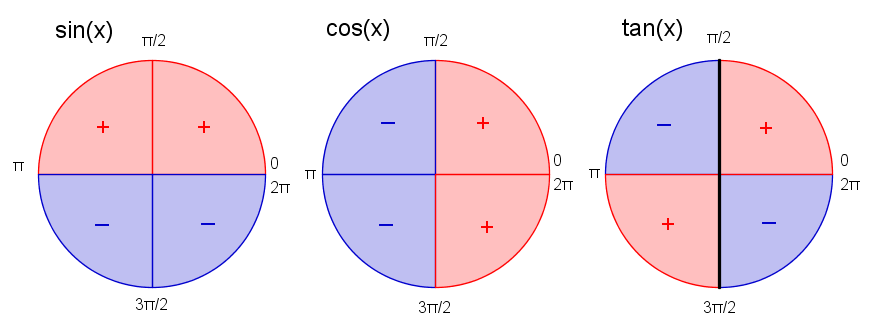
Fortegn av trigonometriske funksjoner

Dette diagrammet viser fortegnene til de forskjellige trigonometriske funksjonene for forskjellige vinkler. Den sorte streken gjennom tangensdiagrammet viser vinklene der $\tan x$ går mot $\pm \mathrm{\infty }$. Vi får et bruddpunkt, og det er derfor meningsløst å snakke of fortegnet til $\tan x$ når $x=\frac{\pi }{2}$ eller $x=\frac{3\pi }{2}$.

Hvis du kan disse diagrammene utanat, vil du kunne vurdere hvilke løsninger du forventer til trigonometriske ligninger. Det vil bli lettere å vurdere om løsningene stemmer.

Noen viktige verdier av sin x, cos x og tan x

Verdiene i tabellen under bør du memorisere. Å kunne disse utenat vil være til stor hjelp i løsingen av trigonometriske ligninger.

Viktige trigonometriske identiteter

Ettersom alle de trigonometriske funksjonene er periodiske, vil de samme verdiene gå igjen for hver syklus. Generellt gjelder det at

$\sin (x+2\pi )=\sin x$

$\cos (x+2\pi )=\cos x$

$\tan (x+\pi )=\tan x$

Å være klar over disse sammenhengene vil ha betydning når vi senere vurderer løsninger av trigonometriske ligninger.

Ut ifra figuren om definisjonen av sinus og cosinus kan vi se flere egenskaper ved funksjonene. Spesifikt,

$\sin (\pi -x)=\sin x$

$\sin (-x)=-\sin x$

$\cos (2\pi -x)=\cos x$

$\tan (-x)=-\tan x$

De trigonometriske funksjonene har mange viktige relasjoner med hverandre. Noe som gjelder per definisjon for sinus og cosinus er identiteten

${\sin }^{2}x+{\cos }^{2}x=1$

som lett kan vises geometrisk med Pythagorassetningen, se figuren om definisjonen av sinus og cosinus.Denne identiteten er viktig fordi den lar oss omforme sinus til cosinus og omvendt.

Som vi senere skal se, henger også tangens sammen med cosinus på følgende måte:

${\tan }^{2}x+1=\frac{1}{{\cos }^{2}x}$

Denne identiteten beviser vi lenger nede i artikkelen.

Inverse trigonometriske funksjoner

Vi definerer de inverse trigonometriske funksjonene $\arcsin$, $\arccos$ og $\arctan$ slik at

$\arcsin (\sin x)=x,x\in [-\frac{\pi }{2},\frac{\pi }{2}]$

$\arccos (\cos x)=x,x\in [0,\pi ]$

$\arctan (\tan x)=x,x\in \text{<}-\frac{\pi }{2},\frac{\pi }{2}$

Dersom $x$ ikke befinner seg i disse mengdene, vil du likevel få en verdi innenfor disse mengdene. Ha dette i bakhodet når du løser trigonometriske ligninger på kalkulator.

I mange lærebøker i den videregående skole, og på kalkulatoren er notasjonen slik:

$arcsinx=si{n}^{-1}x,arccosx=co{s}^{-1}x,arctanx=ta{n}^{-1}x$

Sumformelen for sin x og cos x

Hvis vi vet verdien av sinus og cosinus til to forskjellige vinkler, kan vi finne sinus og cosinus til summen av vinklene. Vi vet at

$\sin (v\pm u)=\sin v\cos u\pm \cos v\sin u$

og

$\cos (v\pm u)=\cos v\cos u\mp \sin v\sin u$

Også disse identitetene kan bevises geometrisk.

Spesialtilfellet $u=v$ er verdt å merke seg, siden disse av og til dukker opp i ligninger:

$\sin (2v)=2\sin v\cos v$

$\cos (2v)={\cos }^{2}v-{\sin }^{2}v$

Trigonometriske ligninger

Trigonometriske ligninger er ligninger der trigonometriske funksjoner av variabler inngår. Disse er nyttige i mange abstrakte og fysiske situasjoner.

I denne seksjonen presenteres løsningsmetoder for de forskjellige typene trigonometriske ligninger.

Løsninger og definisjonsmengde

I mange trigonometriske ligninger er definisjonsmengden til variabelen gitt på forhånd. Definisjonsmengden har innflytelse ikke bare på hva løsningene er, men også hvor mange løsninger som finnes. Dersom det ikke er gitt noen definisjonsmengde kan variabelen ha enhver reell verdi. For å få med alle løsninger bruker vi et lite triks, som vi viser nedenfor.

Når definisjonsmengden er gitt, bør du først se om du kan forhåndsbestemme hvor mange løsninger du forventer å få. Gitt at ligningen er løselig er det akseptabelt å forvente to løsninger per $2\pi$-syklus av de trigonometriske funksjonene. Her er et eksempel:

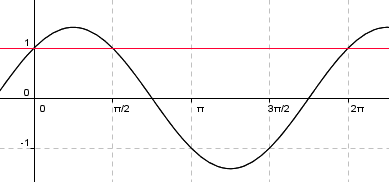
Eksempel

Bildet viser en plott av funksjonen $f(x)=3\sin (2x)+2\cos (2x)+1$. Nullpunktene til funksjonen, markert med grå prikker, viser løsningene til ligningen $3\sin (2x)+2\cos (2x)=-1$. Hvis definisjonsmengden er $x\in [0,\pi >$, går funksjonene gjennom én $2\pi$-syklus, og vi får 2 løsninger. Hvis definisjonsmengden er $x\in [0,2\pi >$, går funksjonene gjennom to $2\pi$-sykluser, og nå får vi 4 løsninger.

OBS!

Regelen om 2 løsninger per syklus gjelder bare hvis vi kan uttrykke ligningen ved én enkelt trigonometrisk funksjon, og denne ikke har sin største eller minste verdi. Som vi skal se senere kan funksjonen over beskrives på formen $f(x)=A\sin (x+\varphi )+d$.

Trigonometriske grunnligninger

Trigonometriske ligninger som kun involverer én trigonomatrisk funksjon, kaller vi trigonometriske grunnligninger. Dise er de enkleste trigonometriske ligningene å løse, og krever kun kunnskap om de trigonometriske funksjonenes inverser.

Løsningsmetode for trigonometriske grunnligninger

Vi tar for oss ligningen

$a\sin (bx)=c$

Vi vil løse denne ligninger for $x$. Det første vi gjør er å isolere $\sin (bx)$ på venstresiden:

$\sin (bx)=\frac{c}{a}$

Siden høyresiden er lik venstresiden, vil $\arcsin$ av høyresiden være lik $\arcsin$ av venstresiden. Altså:

$\arcsin (\sin (bx))=\arcsin (\frac{c}{a})$

Dette gir oss to uttrykk for $x$:

$bx=\arcsin (\frac{c}{a})\vee \pi -bx=\arcsin (\frac{c}{a})$ (Se seksjonen om trigonometriske identiteter)

Sinus er periodisk i $2\pi$ så vi må legge til en vilkårlig multippel av $2\pi$ på hver side.

$bx+k\cdot 2\pi =\arcsin (\frac{c}{a})\vee \pi -bx+k\cdot 2\pi =\arcsin (\frac{c}{a}),k\in \mathbb{Z}$

Når vi isolerer $x$ på venstresiden får vi

$x=\frac{\arcsin (\frac{c}{a})-k\cdot 2\pi }{b}\vee x=\frac{\arcsin (\frac{c}{a})-\pi (2k+1)}{b},k\in \mathbb{Z}$

Det er ikke meningen at du skal pugge disse løsningene, men du bør gjøre deg kjent med fremgangsmåten for å løse slike ligninger. Den samme fremgangsmåten kan benyttes på trigonometriske grunnligninger med $\cos$ og $\tan$ også, men husk at disse har litt forskjellige egenskaper, så løsningene blir ikke de samme.

Test deg selv

Homogene kompositte trigonometriske ligninger

Kompositte trigonometriske ligninger er ligninger der flere trigonometriske funksjoner av variabler kommer fram i ligningene. Den største delen av løsingsprosessen består da av å få ligningen over på en form der den kan løses, det vil si en trigonometrisk grunnligning. Da får vi bruk for identitetene vi lærne lenger oppe (se seksjonene om viktige trigonometriske identiteter og sumformlene). Denne seksjonen går ut på å forklare metodene vi har til rådighet for å oppnå dette.

Homogenitet betyr at konstantene i ligningen forenkles til null. Vi får en kombinasjon av trigonometriske funksjoner er lik null.

Eksempel: Faktorisering

Når vi skal løse trigonometriske ligninger må vi ofte dele den opp i flere trigonometriske grunnligninger før vi kan løse den. Et klassisk eksempel er faktoriseringsmetoden. Vi tar for oss ligningen

$\sin x\cos x-cosx=0,x\in [0,2\pi >$

Selv om det kan være fristende, må du, uansett hva du gjør, ikke dele på $\cos x$. Generellt prøver man å ikke dele eller multiplisere med funksjoner av variabler, fordi du kan miste løsninger, eller lage falske løsninger. Dette gjelder generellt når du deler på null eller multipliserer med null. Istedet faktoriserer vi ligningen:

$\cos x(\sin x-1)=0$

Nå ser vi at for at ligningen skal oppfylles, må $\cos x=0$ eller $\sin x-1=0$. Vi har klart å redusere den kompositte trigonometriske ligningen til to trigonometriske grunnligninger.

$\sin x=1\Rightarrow x=\frac{\pi }{2}$

$\cos x=0\Rightarrow x=\frac{\pi }{2}\vee x=\frac{3\pi }{2}$

Vi presenterer løsningene som en løsningsmengde $x\in L$:

$\text{Missing or unrecognized delimiter for left}$

NB: Dersom du på forhånd har sjekket at det du deler eller multipliserer med ikke er lik null, er det greit å gjennomføre operasjonen. Dette kan gjøres ved å plugge inn null for den aktuelle faktoren og se om likningen oppfylles.

Eksempel: Polynomer

Vi har lært i R1 og T1 hvordan vi løser polynomligninger, så hvis vi kan få en trigonometrisk ligning på polynomform, kan vi løse denne med de samme metodene. La oss si at vi får ligningen

${\sin }^{2}x+\sin x-1=0,x\in [0,2\pi >$

Denne vet vi vet å løse med annengradsformelen. Da får vi to trigonometriske grunnligninger:

$\sin x=\frac{\sqrt{5}-1}{2}$

$\sin x=\frac{\sqrt{5}+1}{2}$

Merk at $\frac{\sqrt{5}+1}{2}>1$, altså har ikke denne grunnligningen noen løsninger. Vi står igjen med kun den første trigonometriske grunnligningen. Når vi løser denne, får vi

$\text{Missing or unrecognized delimiter for left}$

Polynomer av trigonometriske funksjoner av høyere grad enn 2 er verre, ettersom heltallsverdier er sjeldne. Se da etter om ligningen kan faktoriseres.

Eksempel: Omforming

Når vi får en ligning hender det ofte at det ikke finnes noen umiddelbar løsning. De trigonometriske funksjonene lar seg ikke faktorisere, og de er ikke på polynomform. Likevel kan det finnes transformasjoner eller identiteter som lar oss få ligningen over i en slik form. Det kan lære lurt å repetere trigonometriske identiteter og sumformlene på dette tidspunktet. Her skal vi vise to eksempler:

Eksempel 1:

$\sin x+2co{s}^{2}x=1,x\in [0,2\pi >$

Vi kjenner identiteten ${\sin }^{2}x+{\cos }^{2}x=1$. Den kan vi bruke her for å omforme ligningen til

$\sin x+2-2{\sin }^{2}x=1$

$2{\sin }^{2}x-\sin x-1=0$

Dette er en andregradslikning i $\sin x$, som vi kan løse:

$\sin x=\frac{1\pm \sqrt{1+8}}{4}=\frac{1\pm 3}{4}$

$\sin x=\frac{1+3}{4}=1\vee \sin x=\frac{1-3}{4}=-\frac{1}{2}$

$\sin x=1\Rightarrow x=\frac{\pi }{2}$

$\sin x=-\frac{1}{2}\Rightarrow x=\frac{7\pi }{6}\vee x=\frac{11\pi }{6}$

$\text{Missing or unrecognized delimiter for left}$

Eksempel 2:

$\tan x+\sin 2x=0,x\in [0,4\pi >$

Her har vi trigonometriske funksjoner av forskjellige perioder i samme likning. Det er en ganske sikkert hint om at vi kommer til å få bruk for sumformlene. Vi begynner med å skrive om $\tan x$ ved hjelp av definisjonen av tangens:

$\frac{\sin x}{\cos x}+\sin 2x=0$

Nå kan vi trekke $\sin 2x$ fra begge sider av likhets tegnet.

$\frac{\sin x}{\cos x}=-\sin 2x$

Ettersom vi har $\cos x$ i nevneren er det underforstådt at $\cos x\ne 0$, så vi kan multiplisere begge sider av likhetstegnet med $\cos x$. Nå har vi

$\sin x=-\sin 2x\cos x$

Hvis vi nå begynner oss av sumformelen $\sin 2x=2\sin x\cos x$, kan vi omforme ligningen til

$\sin x=-\sin x{\cos }^{2}x$

Hvis vi nå legger til $\sin x{\cos }^{2}x$ på hver side av likhetstegnet, får vi

$\sin x{\cos }^{2}x+\sin x=0$

Og nå ser vi at vi kan faktorisere uttrykket og få noen trigonometriske grunnligninger:

$\sin x({\cos }^{2}x+1)=0\iff \sin x{\sin }^{2}x=0\iff {\sin }^{3}x=0\iff \sin x=0$

$\sin x=0\Rightarrow x=k\cdot \pi ,k\in \mathbb{Z}$

De tre $k$-verdiene som gjør at $x$ faller innenfor definisjonsmengden $[0,4\pi >$ er $k=0$, $k=1$, $k=2$ og $k=3$. Altså får vi løsningsmengden

$\text{Missing or unrecognized delimiter for left}$

Likninger av typen asinx + bcosx = 0

Løses ved å dividerer begge sider av likningen med cosx

Eksempel

Likninger av typen asinx + bcosx = 0

Løses ved å dividerer begge sider av likningen med cosx

Test deg selv

Likninger av typen

:::$a{\sin }^{2}x+bsinxcosx+cco{s}^{2}x=0$

Løses ved å dividerer begge sider av likningen med:

$co{s}^{2}x$

Test deg selv

Likninger av typen

$a{\sin }^{2}x+bsinxcosx+cco{s}^{2}x=d$

Løses ved å sette:

$d\cdot 1=d\cdot (co{s}^{2}x+si{n}^{2}x)$

Likninger av typen

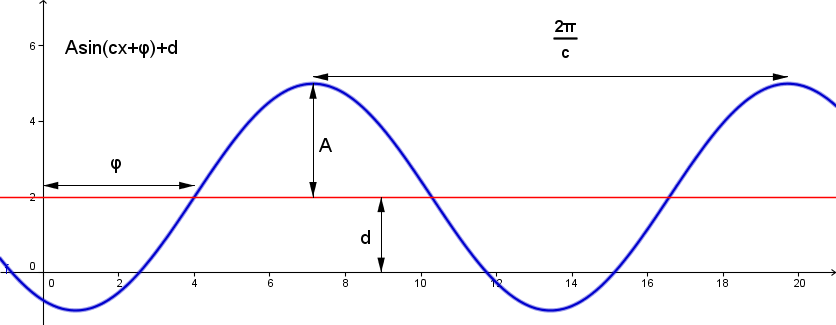
$a\sin cx+bcoscx=d$

Løses ved å skrive om til:

$Asin(cx+\phi )=d$ der $A=\sqrt{a^2+b^2}$ og $\phi$ er gitt ved$\phi =\frac{b}{a}$ og $\phi$ligger i samme kvadrant som (a,b).

Eksempel:

$sinx+cosx=1$

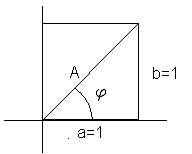
$$\begin{gathered} A=\sqrt{a^2+b^2}=\sqrt{2} \\ a=b=1 \end{gathered}$$

Vinkelen $\phi$ ligger i første kvadrant, $\phi =ta{n}^{-1}(1)=\frac{\pi }{4}$

Vi får

$\sqrt{2}sin(x+\frac{\pi }{4})=1$

Test deg selv

Sammentrekning av sin og cos

Derivasjon av trigonometriske funksjoner

I denne seksjonen skal vi gi beviser for formlene for derivasjon av de trigonometriske funksjonene.

Derivasjon av sin x

$\frac{d}{dx}\sin x=\underset{\mathrm{\Delta }x\to 0}{lim}\frac{\sin (x+\mathrm{\Delta }x)-\sin x}{\mathrm{\Delta }x}$

Vi bruker sumformelen for sinus og ekspanderer den venstre sinusfunksjonen.

$\underset{\mathrm{\Delta }x\to 0}{lim}\frac{\sin x\cos \mathrm{\Delta }x+\cos x\sin \mathrm{\Delta }x-\sin x}{\mathrm{\Delta }x}$

Vi faktoriserer:

$\underset{\mathrm{\Delta }x\to 0}{lim}\frac{\sin x(\cos \mathrm{\Delta }x-1)+\cos x\sin \mathrm{\Delta }x}{\mathrm{\Delta }x}$

Vi har nå en sum av to genseverdier:

$\underset{\mathrm{\Delta }x\to 0}{lim}\sin x\frac{\cos \mathrm{\Delta }x-1}{\mathrm{\Delta }x}+\cos x\frac{\sin \mathrm{\Delta }x}{\mathrm{\Delta }x}$

Det kan bevises geometrisk at

$\underset{\mathrm{\Delta }x\to 0}{lim}\frac{\cos \mathrm{\Delta }x-1}{\mathrm{\Delta }x}=0$

og at

$\underset{\mathrm{\Delta }x\to 0}{lim}\frac{\sin \mathrm{\Delta }x}{\mathrm{\Delta }x}=1$

Resultatet blir da at

$\frac{d}{dx}\sin x=\cos x$

Derivasjon av cos x

$\frac{d}{dx}\cos x=\underset{\mathrm{\Delta }x\to 0}{lim}\frac{\cos (x+\mathrm{\Delta }x)-\cos x}{\mathrm{\Delta }x}$

Vi bruker sumformelen og ekspanderer den venstre cosinusfunksjonen.

$\underset{\mathrm{\Delta }x\to 0}{lim}\frac{\cos x\cos \mathrm{\Delta }x-\sin x\sin \mathrm{\Delta }x-\cos x}{\mathrm{\Delta }x}$

Vi faktoriserer.

$\underset{\mathrm{\Delta }x\to 0}{lim}\frac{\cos x(\cos \mathrm{\Delta }x-1)-\sin x\sin \mathrm{\Delta }x}{\mathrm{\Delta }x}$

Vi har nå en sum av to grenseverdier:

$\underset{\mathrm{\Delta }x\to 0}{lim}\cos x\frac{\cos \mathrm{\Delta }x-1}{\mathrm{\Delta }x}-\sin x\frac{\sin \mathrm{\Delta }x}{\mathrm{\Delta }x}$

Disse grenseverdiene er de samme som vi støtte på i beviset av derivasjonen av sinusfunksjonen. Dermed blir resultatet at

$\frac{d}{dx}\cos x=-\sin x$

Derivasjon av tan x

Nå som vi har derivasjonsformlene for sinus og cosinusfunksjonene, kan vi derivere tangensfunksjonen. Til det bruker vi definisjonen av tangens og skriver den som en brøk av sinus og cosinus og bruker brøkregelen.

$\frac{d}{dx}\tan x=\frac{d}{dx}\frac{\sin x}{\cos x}=\frac{\left(\frac{d}{dx}\sin x\right)\cos x-\left(\frac{d}{dx}\cos x\right)\sin x}{{\cos }^{2}x}=\frac{{\cos }^{2}x+{\sin }^{2}x}{{\cos }^{2}x}$

Vi nevnte i seksjonen om trigonometriske identiteter at vi skulle bevise identiteten om tangens og cosinus. Det gjør vi nå. Det er to måter å forenkle brøken over på. Den ene er å trekke sammen sinus og cosinus med ${\sin }^{2}x+{\cos }^{2}x=1$. Den andre er å separere brøken.

$\frac{{\cos }^{2}x+{\sin }^{2}x}{{\cos }^{2}x}=\frac{1}{{\cos }^{2}x}$

$\frac{{\cos }^{2}x+{\sin }^{2}x}{{\cos }^{2}x}=\frac{{\sin }^{2}x}{{\cos }^{2}x}+\frac{{\cos }^{2}x}{{\cos }^{2}x}={\tan }^{2}x+1$

Ettersom disse uttrykkene åpenbart må være like, har vi bevist identiteten.

Resultatet av derivasjonen er

$\frac{d}{dx}\tan x={\tan }^{2}x+1$

og

$\frac{d}{dx}\tan x=\frac{1}{{\cos }^{2}x}$

---

Tilbake til R2 Hovedside