Del 1

Oppgave 1

a)

1) $f (x) = 2 \sin (2 x) \Rightarrow f^{'} (x) = 4 \cos (2 x)$

2) $g (x) = x^{2} \cos (2 x) \Rightarrow g^{'} (x) = (x^{2})^{'} \cos (2 x) + x^{2} (\cos (2 x))^{'} = 2 x \cos (2 x) - 2 x^{2} \sin (2 x)$

3) $h (x) = \frac{1}{2} \sqrt{x^{2} - 4 x} \Rightarrow h^{'} (x) = \frac{1}{2} \frac{x - 2}{\sqrt{x^{2} - 4 x}}$

b)

1) Delvis integrasjon gir at $\int x e^{x} d x = [x e^{x}] - \int e^{x} d x = (x - 1) e^{x} + C$

2) $\int \frac{5 x + 3}{x^{2} - 9} d x = \int \frac{5 x + 3}{(x - 3) (x + 3)} d x$ . Delbrøksoppspaltning gir at

$\frac{1}{(x - 3) (x + 3)} = \frac{1}{6} (\frac{1}{x - 3} - \frac{1}{x + 3})$ , så $\int \frac{5 x + 3}{(x - 3) (x + 3)} d x = \int (5 x + 3) \frac{1}{6} (\frac{1}{x - 3} - \frac{1}{x + 3}) d x = \frac{1}{6} (\int \frac{5 x + 3}{x - 3} d x - \int \frac{5 x + 3}{x + 3} d x)$

$\int \frac{5 x + 3}{x - 3} d x = \int \frac{5 (x - 3) + 18}{x - 3} d x = 5 \int d x + 18 \int \frac{1}{x - 3} d x = 5 x + 18 \ln (| x - 3 |) + C_{1}$ og

$\int \frac{5 x + 3}{x + 3} d x = \int \frac{5 (x + 3) - 12}{x + 3} d x = 5 \int d x - 12 \int \frac{1}{x + 3} d x = 5 x - 12 \ln (| x + 3 |) + C_{2}$ , så

$\frac{1}{6} (\int \frac{5 x + 3}{x - 3} d x - \int \frac{5 x + 3}{x + 3} d x) = 3 \ln (| x - 3 |) + 2 \ln (| x + 3 |) + C$

c)

Sirkelen på figuren er beskrevet ved ligningen $x^{2} + y^{2} = 1$ , så høyden opp til halvsirkelen i øvre halvplan som funksjon av $x$ , er $y (x) = \sqrt{1 - x^{2}}$ . Arealet av halvsirkelen i øvre halvplan er derfor $\int_{- 1}^{1} y (x) d x = \int_{- 1}^{1} \sqrt{1 - x^{2}} d x = \frac{1}{2} π (1)^{2} = \frac{1}{2} π$

d)

1) Dersom én av vektorene har lengde $0$ vil prikkproduktet være $0$ . Anta videre at begge vektorene har lengde ulik $0$ . Siden prikkproduktet er $0$ , må vektorene $\vec{a}$ og $\vec{b}$ stå normalt på hverandre.

2) Dersom én av vektorene har lengde $0$ vil kryssproduktet være $0$ . Anta videre at begge vektorene har lengde ulik $0$ . Siden kryssproduktet er $0$ , må vektorene $\vec{a}$ og $\vec{b}$ ligge parallelt.

e)

Beregner først vektorene $\vec{A B} = (2 - 1, - 1 - 1, 3 - (- 1)) = (1, - 2, 4)$ og $\vec{A C} = (3 - 1, 2 - 1, 2 - (- 1)) = (2, 1, 3)$ . Kryssproduktet $\vec{A B} \times \vec{A C} = (- 2 \cdot 3 - (1 \cdot 4), - (1 \cdot 3 - 2 \cdot 4), 1 \cdot 1 - 2 \cdot (- 2)) = (- 10, 5, 5)$ . For å vise at $\vec{A B} \times \vec{A C}$ står vinkelrett på både $\vec{A B}$ og $\vec{A C}$ , beregner vi $(\vec{A B} \times \vec{A C}) \cdot \vec{A B}$ og $(\vec{A B} \times \vec{A C}) \cdot \vec{A C}$ og viser at disse er $0$ :

$(\vec{A B} \times \vec{A C}) \cdot \vec{A B} = (- 10, 5, 5) \cdot (1, - 2, 4) = - 10 - 10 + 20 = 0$ og

$(\vec{A B} \times \vec{A C}) \cdot \vec{A C} = (- 10, 5, 5) \cdot (2, 1, 3) = - 20 + 5 + 15 = 0$ .

f)

Induksjonssteg 1: $1 = \frac{4^{1} - 1}{3}$ , så formelen er riktig for $n = 1$

Induksjonssteg 2: Anta at formelen er riktig for $n = k$ , så $1 + 4 + 16 + . . . + 4^{k - 1} = \frac{4^{k} - 1}{3}$ . Da er $1 + 4 + 16 + . . . + 4^{k - 1} + 4^{k} = \frac{4^{k} - 1}{3} + 4^{k} = \frac{4^{k} - 1 + 3 \cdot 4^{k}}{3} = \frac{(1 + 3) 4^{k} - 1}{3} = \frac{4^{k + 1} - 1}{3}$ , så formelen er riktig for $n = k + 1$ , og vi er ferdige.

Oppgave 2

a)

Vi multipliserer den førsteordens differensialligningen $y^{'} - 2 y = 5$ med integrerende faktor $e^{\int - 2 d x} = e^{- 2 x}$ , og får

$e^{- 2 x} y^{'} - 2 e^{- 2 x} y = 5 e^{- 2 x}$ . Venstresiden kan nå omskrives:

$(e^{- 2 x} y)^{'} = 5 e^{- 2 x}$

Vi integrerer ligningen med hensyn på $x$ :

$\int (e^{- 2 x} y)^{'} d x = \int 5 e^{- 2 x} d x e^{- 2 x} y = - \frac{5}{2} e^{- 2 x} + C$ , og løser for $y$ :

$y = - \frac{5}{2} + C e^{2 x}$ . Løsningen verfiseres ved innsetting i den opprinnelige diff.ligningen:

$y^{'} = 2 C e^{2 x}$ , så $y^{'} - 2 y = 2 C e^{2 x} - 2 (- \frac{5}{2} + C e^{2 x}) = 5$ .

b)

1) $y (0) = - \frac{5}{2} + C = 2$ , så $C = 2 + \frac{5}{2} = \frac{9}{2}$

2) Setter inn $y = \frac{49}{2}$ i løsningen, og løser for $x$ :

$\frac{49}{2} = - \frac{5}{2} + \frac{9}{2} e^{2 x} \frac{54}{9} = 6 = e^{2 x} \ln (6) = 2 x x = \frac{\ln (6)}{2} \approx \frac{1.8}{2} = 0.9$

c)

Tangenten i $(0, 2)$ har ligning $y = a x + b$ , der $a = (- \frac{5}{2} + \frac{9}{2} e^{2 x})^{'} (0) = \frac{18}{2} = 9$ . I tillegg må punktet $(0, 2)$ ligge på tangentlinja, så $2 = a \cdot 0 + b$ . Ligningen til tangenten er derfor $y = 9 x + 2$ .

Del 2

Oppgave 3

a)

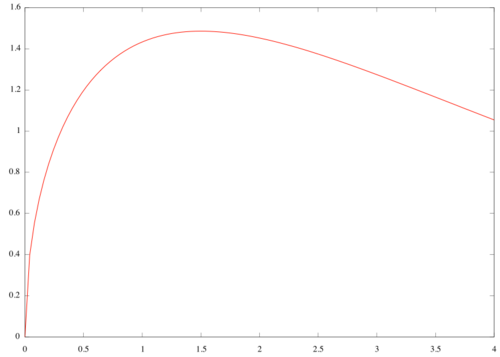
Finner toppunktet ved derivasjon av funksjonen $f (x) = 2 \sqrt{x} e^{- \frac{x}{3}}$ : $f^{'} (x) = \frac{(3 - 2 x) e^{- \frac{x}{3}}}{3 \sqrt{x}}$ . Den deriverte er $0$ når $3 - 2 x = 0$ , så toppunktet er i $x = \frac{3}{2}$ . Diameteren til skaftet er størst i toppunktet til grafen til $f (x)$ . Størst mulig diameter er derfor $2 \cdot f (\frac{3}{2}) = 4 \sqrt{\frac{3}{2}} e^{- \frac{1}{2}} \approx 2.97$

b)

Volumet er gitt ved $\int_{0}^{4} π f (x)^{2} d x = 4 π \int_{0}^{4} x e^{- \frac{2}{3} x} d x =$ . La $u = - \frac{2}{3} x$ . Integralet blir $9 π \int u e^{u} d u$ . Vi bruker resultatet fra oppgave 1b),1): $9 π \int u e^{u} d u = 9 π [(u - 1) e^{u}] = 9 π [(- \frac{2}{3} x - 1) e^{- \frac{2}{3} x}]_{0}^{4} = 9 π ((- \frac{8}{3} - 1) e^{- \frac{8}{3}} + 1) = 9 π (- \frac{11}{3} e^{- \frac{8}{3}} + 1)$

Oppgave 4

a)

1) La $A_{0} = A$ og $B_{0} = B$ . Generelt kan vi skrive arealet av trapeset $A_{n} B_{n} B_{n + 1} A_{n + 1}$ som $(A_{n} B_{n} + A_{n + 1} B_{n + 1}) \frac{B_{n} B_{n + 1}}{2}$ , der $A_{0} B_{0} = 8$ , $B_{0} B_{1} = 8$ , $B_{n} B_{n + 1} = \frac{16}{2^{n + 1}}$ , $\frac{A_{n} B_{n}}{B_{n} B_{n + 1}} = \frac{8}{8} = 1$ (ved formlikhet av trapesene). Altså er $A_{n} B_{n} = B_{n} B_{n + 1} = \frac{16}{2^{n + 1}}$ og arealet av trapeset $A_{n} B_{n} B_{n + 1} A_{n + 1}$ blir $(A_{n} B_{n} + A_{n + 1} B_{n + 1}) \frac{B_{n} B_{n + 1}}{2} = (\frac{16}{2^{n + 1}} + \frac{16}{2^{n + 2}}) \frac{16}{2^{n + 2}} = \frac{3 \cdot 16^{2}}{2^{2 n + 4}} = 3 \cdot 2^{4 - 2 n}$ . Summen av arealene til trapesene blir derfor

$\sum_{n = 0}^{\infty} 3 \cdot 2^{4 - 2 n} = 48 + 12 + 3 + . . .$

2) Fra forrige deloppgave ser vi at summen av arealene er en geometrisk rekke

$\sum_{n = 0}^{\infty} 3 \cdot 2^{4 - 2 n} = 48 \sum_{n = 0}^{\infty} (\frac{1}{4})^{n}$

Rekken konvergerer siden $| \frac{1}{4} | < 1$

b)

Geometrisk ser vi at summen av arealene må konvergere mot arealet av trekanten $A B C$ , som er $\frac{8 \cdot 16}{2} = 64$

Summeformelen for en geometrisk rekke $\sum_{k = 0}^{n - 1} a r^{k} = a \frac{1 - r^{n}}{1 - r}$ gir at

$lim_{n \to \infty} \sum_{k = 0}^{n - 1} 48 (\frac{1}{4})^{k} = 48 lim_{n \to \infty} \frac{1 - {\frac{1}{4}}^{n}}{\frac{3}{4}} = 48 \cdot \frac{4}{3} = 64$

Oppgave 5

a)

I $x y$ -planet er $z = 0$ , så vi må ha at $0 = 4 + 2 t$ . Altså er $t = - 2$ i punkt $A$ . I $x z$ -planet er $y = 0$ , så vi må ha at $0 = 3 + t$ . Altså er $t = - 3$ i punkt $B$ . Koordinatene til $A$ og $B$ er derfor gitt ved $A (5 + 2 \cdot 2, 3 - 2, 0) = A (9, 1, 0)$ og $B (5 - 2 \cdot (- 3), 0, 4 + 2 \cdot (- 3)) = B (11, 0, - 2)$ . Avstanden mellom $A$ og $B$ er derfor $| (11 - 9, 0 - 1, - 2 - 0) | = | (2, - 1, - 2) | = \sqrt{2^{2} + 1^{2} + 2^{2}} = \sqrt{9} = 3$

b)

Vi kan skrive linja $l$ på formen $(x, y, z) = (5 - 2 t, 3 + t, 4 + 2 t) = (5, 3, 4) + t (- 2, 1, 2)$ . Det betyr at vektoren $(- 2, 1, 2)$ angir retningen til linja $l$ . På samme måte kan linja $m$ skrives som $(x, y, z) = (s, 1 - s, 1 + s) = (0, 1, 1) + s (1, - 1, 1)$ , der vektoren $(1, - 1, 1)$ angir retningen. Linjene er parallelle hvis og bare hvis det fins en konstant $k$ slik at $(- 2, 1, 2) = k (1, - 1, 1)$ . Utfra ligningen ser vi at det ikke fins en slik $k$ , altså er linjene ikke parallelle.

c)

Et tilfeldig punkt P på l er angitt ved koordinatet $(x, y, z) = (5 - 2 t, 3 + t, 4 + 2 t)$ , og et punkt Q på m er gitt ved $(x, y, z) = (s, 1 - s, 1 + s)$ . $\vec{P Q} = (s, 1 - s, 1 + s) - (5 - 2 t, 3 + t, 4 + 2 t) = (s + 2 t - 5, - s - t - 2, s - 2 t - 3)$

d)

For at $\vec{P Q}$ skal stå vinkelrett på linjene $m$ og $l$ , må $(s + 2 t - 5, - s - t - 2, s - 2 t - 3) \cdot (- 2, 1, 2) = 0 = (s + 2 t - 5, - s - t - 2, s - 2 t - 3) \cdot (1, - 1, 1)$ . Vi får dermed ligningene $- 2 s - 4 t + 10 - s - t - 2 + 2 s - 4 t - 6 = - s - 9 t + 2 = 0$ og $s + 2 t - 5 + s + t + 2 + s - 2 t - 3 = 3 s + t - 6 = 0$ . Altså er $3 s + t - 6 - 3 s - 27 t + 6 = - 26 t = 0$ , så vi må ha at $t = 0$ . Da er $s = 2$ . Vi får da punktene $P (5, 3, 4)$ og $Q (2, - 1, 3)$

e)

$| \vec{P Q} | = | (2, - 1, 3) - (5, 3, 4) | = | (- 3, - 4, - 1) | = \sqrt{3^{2} + 4^{2} + 1^{2}} = \sqrt{9 + 16 + 1} = \sqrt{26}$

Oppgave 6

a)

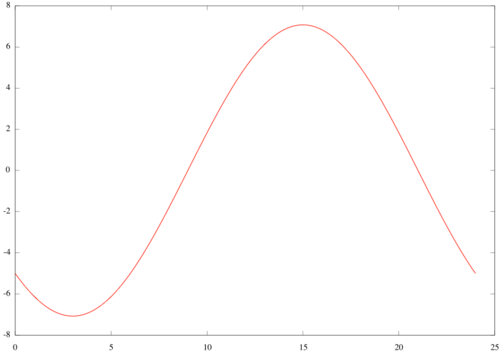
Avleser fra figuren at amplituden er $\approx 7$ , og perioden $24$ .

b)

Den deriverte av $f (x)$ er $f^{'} (x) = - \frac{5}{12} π (\cos (\frac{π}{12} x) - \sin (\frac{π}{12} x))$ , og har nullpunkt i $x = 3$ og $x = 15$ . Den deriverte er positiv når $3 < x < 15$ , så funksjonen $f (x)$ har toppunkt i $x = 15$ og bunnpunkt i $x = 3$ .

c)

Vi ser at $g (x) = 22 + f (x)$ . Funksjonene $f (x)$ og $g (x)$ må derfor ha topp- og bunnpunkter i samme (korresponderende) x-verdier. Laveste temperatur inntreffer for $x = 3$ . Da er temperaturen $g (3) = 22 - 5 \sin (\frac{3 π}{12}) - 5 \cos (\frac{3 π}{12}) = 22 - 5 \sqrt{2} \approx 14.93$ grader Celsius. Høyeste temperatur inntreffer for $x = 15$ . Da er temperaturen $g (15) = 22 - 5 \sin (\frac{15 π}{12}) - 5 \cos (\frac{15 π}{12}) = 22 + 5 \sqrt{2} \approx 29.07$ grader Celsius.

Oppgave 7

a)

b)

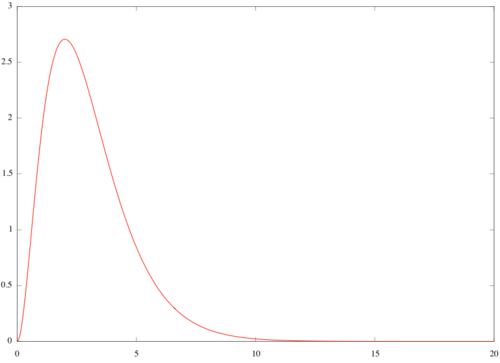
1) La $f (x) = 5 x^{2} e^{- x}$ . Produktregelen gir at $f^{'} (x) = (5 x^{2})^{'} e^{- x} + 5 x^{2} (e^{- x})^{'} = 10 x e^{- x} - 5 x^{2} e^{- x} = 5 (2 x - x^{2}) e^{- x}$ . (Vi har i tillegg brukt kjerneregelen, og derivasjonsreglene $(e^{x})^{'} = e^{x}$ og $(x^{n})^{'} = n x^{n - 1}$ ).

2) Eksponentialfunksjonen er alltid positiv, så det er tilstrekkelig å betrakte nullpunktene til $2 x - x^{2} = x (2 - x)$ i uttrykket for den deriverte, som er $x = 0$ og $x = 2$ . Når $0 < x < 2$ er $f^{'} (x) > 0$ og når $x > 2$ er $f^{'} (x) < 0$ , så funksjonen $f (x)$ vokser i intervallet $(0, 2)$ og avtar i $(2, \infty)$ . $f (x)$ har derfor et toppunkt i $x = 2$ , men ingen bunnpunkt.

c)

$\begin{aligned} (- 5 x^{2} e^{- x} - 10 x e^{- x} - 10 e^{- x} + C)^{'} & = (- 5 x^{2} e^{- x})^{'} - (10 x e^{- x})^{'} - (10 e^{- x})^{'} + C^{'} \\ = - 10 x e^{- x} + 5 x^{2} e^{- x} - 10 e^{- x} + 10 x e^{- x} + 10 e^{- x} + 0 \\ = 5 x^{2} e^{- x} \\ = f (x) \end{aligned}$

d)

$lim_{a \to \infty} \int_{0}^{a} f (x) d x = lim_{a \to \infty} [- 5 x^{2} e^{- x} - 10 x e^{- x} - 10 e^{- x}]_{0}^{a} = lim_{a \to \infty} - 5 a^{2} e^{- a} - 10 a e^{- a} - 10 e^{- a} + 10$

Fra det som er oppgitt i oppgaven vil de tre første leddene gå mot $0$ , så det eneste som gjenstår er det siste leddet, altså er $lim_{a \to \infty} \int_{0}^{a} f (x) d x = 10$

R2 2011 vår LØSNING