Løsning del 1 og del 2 utrinn Vår 15
Løsningsforslag del 1 og 2 laget av MKH I oppg 16 del 1 skal det stå 900 og ikke 90 som i løsningsforslaget I oppg 6 del 2 skal rett benevning være m^3
DEL EN
Oppgave 1
a)
$395+1988 = 2383$
b)
$572-479 = 93$
c)
$102 \cdot 98 = 9996$
d)
$81: 0,27 = \\ 8100:27 = 300$
Oppgave 2
a)
98km = 9,8 mil
b)
12,3 kg = 123 hg
c)
800 ml = 0,8 L
d)
4h 12min = 4,2 h
Oppgave 3
a)
$435000 = 4,35 \cdot 10^5$
b)
$ 105 = 3 \cdot 5 \cdot 7 $
Oppgave 4
a)
$\frac{3}{10} + \frac{2}{10} = \frac{3+2}{10} = \frac{5}{10} = \frac 12 $
b)
$\frac{7}{12} - \frac{1}{3} = \frac{7}{12} - \frac{1 \cdot 4}{3 \cdot 4} = \frac {7-4}{12} = \frac{3}{12} = \frac 14$
c)
$\frac{8}{9} \cdot \frac{3}{4} \cdot \frac{1}{2} = \frac{\not{8} \cdot \not{3} \cdot 1}{\not{9} \cdot 3 \cdot \not 4 \cdot \not 2} = \frac 13$
d)
$\frac{4}{5}: \frac{6}{15}= \\ \frac{4}{5} \cdot \frac{15}{6} = \\ \frac{4 \cdot 15}{5 \cdot 6}= \\ \frac{}{} \\ \frac{4 \cdot \not{15} \cdot \not{3}}{\not 5 \cdot \not 6 \cdot 2} =2$
Oppgave 5
a)
$6x=4x+8 \\ 6x-4x=8 \\ 2x=8 \\ x=4$
b)
$\frac x2 - \frac{x-2}{3} = 1 \quad | \cdot 6 \\ 3x-2(x-2)= 6 \\ 3x-2x+4 =6 \\x = 2$
Oppgave 6
Målestokk 1:50000.
$\frac{1}{50000} = \frac{4,5cm}{x} \\x= 50000 \cdot 4,5cm \\ x=225000 cm = 2250m = 2,25 km$
2,25 km er riktig svar.
Oppgave 7
Butikk A: $100 \cdot 0,8 = 80$ kroner
Butikk B: $(100 \cdot 0,9) \cdot 0,9 = 90 \cdot 0,9 = 81$ kroner.
Varen er en krone billigere i butikk A.
Oppgave 8
a)
$2-2(2a+1) \\ =2-4a-2 \\ = - 4a$
b)
$\frac{2a-2b)(a+b)}{2a+2b)} =\\ \frac{2(a-b)(a+b)}{2(a+b)} = \\ a-b$
Oppgave 9
a)
$\frac 14 = 25$%
Det er 25% sannsynlig at han trekker Avatar.
b)
Sannsynlighet for at Gravity er med:
Tenker at man trekker en film av fire, så en film av tre. Gravity kan bli trukket i den første eller den andre trekkningen.
$P(film \quad med)=\frac 14 \cdot 1 + \frac 34 \cdot \frac 13 \\ = \frac {3}{12} + \frac {3}{12} = \frac 12$
Alternativt kan man tenke at sannsynligheten for at filmen er med = 1 - sannsynligheten for at den ikke er med. Da blir det slik
$P(film \quad med)= 1- \frac 34 \cdot \frac 23 = \frac 12$
Begge måtene å tenke på gir samme resultat, det er 50% sannsynlig at filmen er med.
Oppgave 10
$V= \frac{\pi r^2h}{3} \\ 3V = \pi r^2 h \\ \pi r^2h = 3V \\ h= \frac{3V}{\pi r^2}$
Oppgave 11
Alder:
Marius = x
Gabriel = 2x
Andreas = 2x+3
$x+2x+2x+3 = 53 \\ 5x=50 \\x=10$
Marius er 10 år, Gabriel er 20 år og Andreas er 23 år.
Oppgave 12
a)
Gjennomsnitt:
$\frac{91+91+74+90}{4} = \frac{346}{4}= 86,5$
Gjennonsnittsvekten er 86,5 kg.
b)
Medianverdi:
74, 90, 91 ,91
Gjennomsnittet av 90 og 91 er 90,5. Medianvekten er 90,5 kg.
Oppgave 13
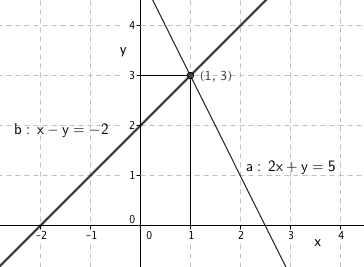
a)
\begin{bmatrix} 2x+y=5 \\ x-y = -2 \end{bmatrix} \begin{bmatrix} 2x+y=5 \\ x = y-2 \end{bmatrix} \begin{bmatrix} 2(y-2)+y=5 \ \\ 2y -4 +y = 5 \ \\ 3y =9 \\ y=3 \end{bmatrix}
\begin{bmatrix} x-y = -2 \\x-3 =-2 \\ x=1 \end{bmatrix}
Likningssystemet har løsning for $x=1 \wedge y=3$
b)
Oppgave 14
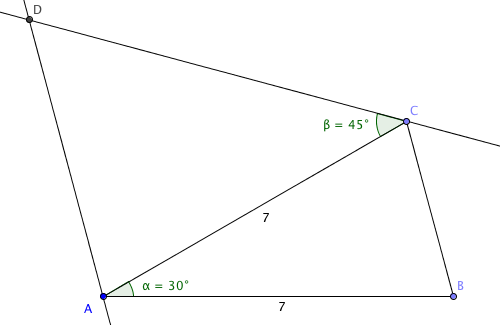
- Avsetter linjestykket AB, 7 cm.
- Konstruerer 30 grader i A.
- Avsetter 7 cm på ny linje og merker av C.
- Trekker linjestykket BC.
- Konstruerer 45 grader i C, på AC.
- Trekker linjen gjennom C, 45 grader på AC.
- Konstruere en linje gjennom A, parallell med BC.
- I skjæringen mellom de to linjene ligger D.
Oppgave 15
180 meter gjerde skal innhegne et størst mulig areal. Pi settes til $\approx 3$:
Kvadrat:
Gir sidekanter 45 meter. Da blir arealet av kvadratet $45m \cdot 45m = 2025m^2$
Sirkel: Vi må finne radius:
$O= 2\pi r \Rightarrow r= \frac{O}{2 \pi} \\ r= \frac{180m}{2 \cdot 3} \\ r= 30 $
Areal av sirkel: $A= \pi r^2 \\ A= 3 \cdot 30^2 m^2 \\ A= 2700 m^2$
Sirkelen har et større areal enn kvadratet.
Oppgave 16
Likesidet trekant med omkrets 180 meter. En side i trekanten er da 60 meter. Om vi nedfeller normalen fra ett av hjørnen får vi høyden i trekanten, h. Denne er gitt ved Pytagoras:
$h^2 = 60^2 - 30^2 \\ h^2 = 3600 - 900 \\h^2 = 2700 \\ h = \sqrt{2700}\\ h= \sqrt{3 \cdot 9 \cdot 100} \\ h= \sqrt \cdot 3 \sqrt 9 \cdot \sqrt{100} \\ h = 3 \cdot 10 \cdot \sqrt 3 \\h= 30 \sqrt 3 $
Areal av trekant:
$A= \frac{g \cdot h}{2} \\ A= \frac{60 \cdot 30 \sqrt 3}{2} \\ A = 900 \sqrt 3$
Uregning ble gjort uten benevning, men både 60 og $30 \sqrt3 $ er meter, så svaret blir $900 \sqrt 3 m^2$
DEL TO
Oppgave 1
a)
$3,5 \cdot 10 kr + 2 \cdot 12,5 kr + 90 kr = 150 kr$
Hun må betale 150 kroner.
b)
$100 kr - 40 kr = 60 kr \\ \frac{60kr}{12 kr/kg} = 5 kg$
Han kjøper 5 kilogram gullerøtter.
Oppgave 2
a)
$d \approx 24 \cdot 2,54cm \approx 60,96 cm \\ r \approx 30,48 cm \\ O=2\pi r \\ O= 2 \pi \cdot 30,48 cm = 191,5 cm$
Forhjulet har en omkrets på cirka 191,5 centimeter.
b)
Omkrets bakhjul:
$\frac{1,7}{3} = \frac{191,5}{O} \\ 1,7O = 3 \cdot 191,5 \\ O = 337,9 cm $
Bakhjulets diameter:
$O= \pi d \\ d = \frac{337,9 cm}{\pi} \\ d= 107,55 cm \approx \frac{107,55 cm}{2,54} \approx 42" $
Oppgave 3
a)
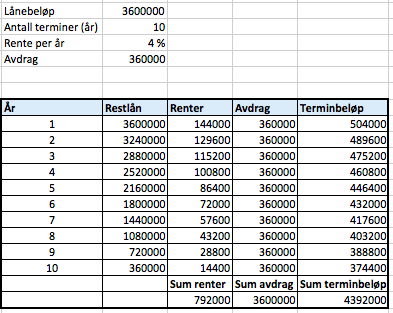
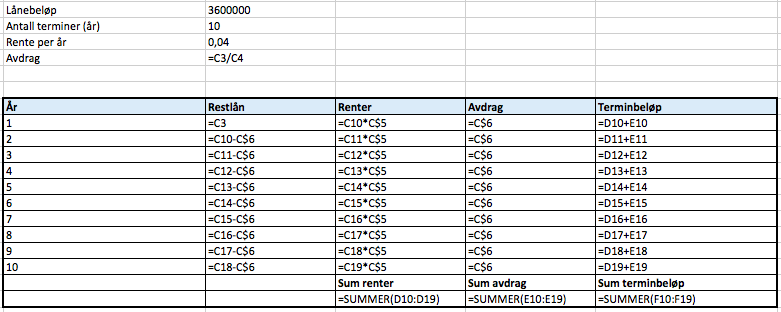
Formler:
b)
c)
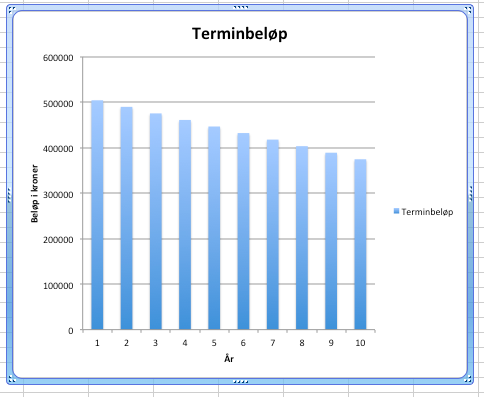
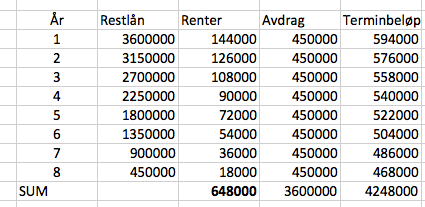
Han betaler $792000 - 648000 = 144000$ mindre i renter, ved å redusere antall terminer til 8.
Oppgave 4
a)
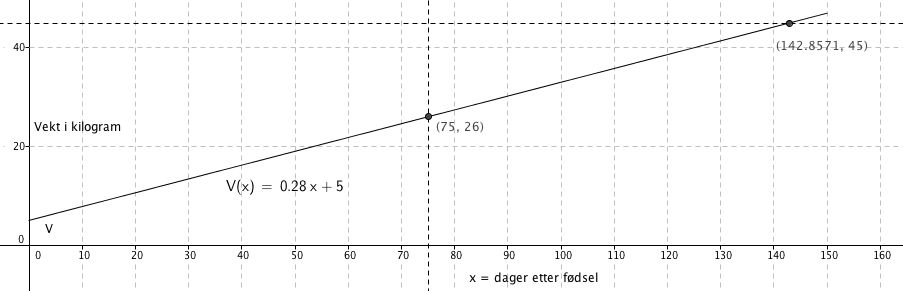
$V(x)=0,28x+5$
Ett nyfødt lam veier ca. 5 kg. ( konstantledd, x = 0)
Vekten øker daglig med stigningstallet, altså 0,28 kg. ( ganske imponerende egentlig, om modellen er riktig da).
b)
c)
Fra Figur i b ser man at vekten etter 75 dager er ca. 26 kilogram. (ca, fordi dette er en modell).
d)
Lammet går en utrygg tilværelse i møte når det er mere enn 143 dager gammelt, dvs. i underkant av fem måneder.
Oppgave 5
a)
Vi har en 30, 60, 90 trekant. Da er hypotenus to ganger lengden av korteste katet.
Vi kaller høyden i trekanten for h. Det vil være det lengste katetet. Vi må huske på å legge til 1,8 meter, som blir treets høyde.
$9^2 + h^2 = 18^2 \\ h = \sqrt{18^2- 9^2} \\ h = 15,59 meter$
Når vi plusser på 1,8 meter finner vi at treets høyde er 17,4 meter.
b)
Bruker formlikhet:
$\frac{1,8}{1,5} = \frac{x}{14,5} \\ x= 17,4$
Treet er fortsatt 17,4 meter høyt.
c)
Bruker pytagoras:
$x^2 + 4,2^2 = (18-x)^2 \\ x^2 + 4,2^2 = 18^2 -36x + x^2 \\36x = 18^2-4,2^2 \\ x= 8,5$
Treet knakk 8,5 meter over bakken.
Oppgave 6
a)
Volum av kjegle:
$V= \frac 13 \pi r^2h = \frac 13 \cdot \pi \cdot 1,05^2 \cdot 1,8 = 2,08 $
Volumet av kjeglen er 2,08 $m^3$.
b)
Volumet av sylinderen er $14,5 m^3 - 2,08 m^3 = 12,42m^3$
Høyden i sylinderen blir da:
$V = \pi r^h \\ h = \frac{V}{\pi r^2}\\ h = \frac{12,42m^3}{\pi \cdot (1,05m)^2} \\ h = 3,59m $
Høyde av silo er høyde av sylinder pluss høyde av kjegle:
$h_{silo} = 3,59m + 1,8 m =5,39 m$
Siloens høyde er 5,39 meter.
c)
$\frac{V_s}{V_k} = \frac{6}{1} \\ \frac{\pi r^2 h_1}{\frac 13 \pi r^2 h_2} = 6 \\ \frac{3h_1}{h_2} = 6 \\ \frac{h_1}{h_2} = 2$
Forholdet mellom høyde i sylinder og høyde i kjegle er 2, eller 2:1.
Oppgave 7
a)
| Antall sideflater - F | Antall hjørner - H | Antall sidekanter - K | |
| Tetraeder | 4 | 4 | 6 |
| Heksaeder | 6 | 8 | 12 |
| Oktaeder | 8 | 6 | 12 |
b)
Tetraeder: F + H - K = 4 + 4 - 6 = 2
Heksaeder: 6 + 8 -12 = 2
Oktaeder: 8 + 6 - 12 = 2
Antall sidekanter på et platonsk legeme er alltid to mindre enn summen av antall sideflater og antall hjørner.
Oppgave 8
a)
Dersom lengden av sidene i et kvadrat er a, er arealet av kvadratet: $A= a^2$. Dersom sidekantene fordobbles i lengde blir lengden 2a. Arealet blir da: $A= (2a)^2 = 4a^2$. Altså firdobbles arealet når sidene i kvadratet dobbles.
b)
AB = x
Areal kvadrat ABCD: $A = x^2$
Bruker pytagoras og finner at lengden av $BD = \sqrt{2x^2}$
Areal av kvadratet BEFD: $A=( \sqrt{2x^2})^2 = 2x^2$
Altså er arealet av BEFD dobbelt så stort som arealet av ABCD.
Oppgave 9
a)
$(n^2-1)^2+(2n)^2 =(n^2+1)^2 \\ n= 6 \quad gir: \\ (6^2-1)^2+(2 \cdot 6)^2 =(6^2+1)^2 \\ 35^2 + 12^2 = 37^2 $
Talltrippelet er ( 12, 35, 37).
b)
Man observerer fra formelen at det minste tallet i talltrippelet er 2n. Siden det minste tallet er 22, må n = 11.
c)
$(n^2-1)^2+(2n)^2 =(n^2+1)^2$
Skal vise at likningen stemmer ved å regne ut venstre og høyre side hver for seg.
Venstre side: $(n^2-1)^2+(2n)^2 =n^4-2n^2+1 + 4n^2 = n^4+2n^2 +1$
Høyre side: $(n^2+1)^2 = n^4 + 2n^2 +1$
Formelen stemmer.