S1 2016 vår LØSNING
Fasit (ikke løsning) laget av matteprat-bruker rekel
Løsning laget av matteprat-bruker LektorH
DEL EN
Oppgave 1
a)
$X^2-3X+2=0 \\ X= \frac{3 \pm \sqrt{9-8}}{2} \\ x=1 \vee x=2$
b)
$lg(4x+3)= lg7 \\ 10^{lg(4x+3)} = 10^{lg7} \\ 4x+3 =7 \\ 4x=4\\ x=1$
Oppgave 2
a)
$(2x-3)^2 -3(x-2)^2 + (x-1)(x+1) = \\ 4x^2-12x+9-3(x^2-4x+4)+x^2-1= \\ 4x^2-12x+9-3x^2+12x-12+x^2-1= \\ 2x^2-4$
b)
$\frac{a^2b^3}{(a^3b)^{-2}} = \frac{a^2b^3}{a{-6}b^{-2}} = a^{2-(-6)}b^{3-(-2)}= a^8b^5$
Oppgave 3
a)
Omkrets: 2x + 2y = 11
Areal: xy=6
<math> \left[ \begin{align*}2x+2y=11\\ xy=6 \end{align*}\right] </math>
b)
<math> \left[ \begin{align*}2x+2y=11\\ xy=6 \end{align*}\right] </math>
<math> \left[ \begin{align*}x=\frac{11}{2}-y\\ xy=6 \end{align*}\right] </math>
$( \frac {11}{2}-y)y=6 \\ -y^2 + \frac{11}{2}y - 6 =0 \\ -2y^2+11y - 12 =0 $
$y = \frac{-11 \pm \sqrt{121 - 96}}{-4} \\ y= \frac{3}{2} \vee y =4$
Innsatt gir det løsninger $( \frac 32, 4) \wedge (4, \frac32 )$ som jo er samme rektangel.
Lenden på rektangelet er 4 og bredden er $\frac 32$.
Oppgave 4
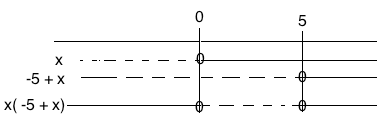
$-5x+x^2 \leq 0 \\ x(-5 + x) \leq 0$
$x \in [0, 5]$
Oppgave 5
a)
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
1 7 21 35 35 21 7 1
$\binom{7}{4} = 35$
Teller ned til syvende rad (første rad er nullte rad), teller så fire mot høyre.
b)
Dersom man skal velge ut fire elementer fra en mengde på syv, uten tilbakelegging, kan det gjøres på 35 måter.
Oppgave 6
a)
Det finne 10 siffer medregnet null. Siden koden ikke kan starte med null får vi:
$9 \cdot 10 \cdot 10 \cdot 10 = 9000$
Det finnes 9000 pinkoder.
b)
Her kan man tenke at et siffer "brukes opp" for hver posisjon vi beveger oss mot høyre. Kan fortsatt ikke ha null i første, men kan ha null etter det. Vi får:
$9 \cdot 9 \cdot 8 \cdot 7= 4536$
Det finnes 4536 pinnkoder som ikke starter med null og som ikke bruker samme siffer flere ganger.
Oppgave 7
a)
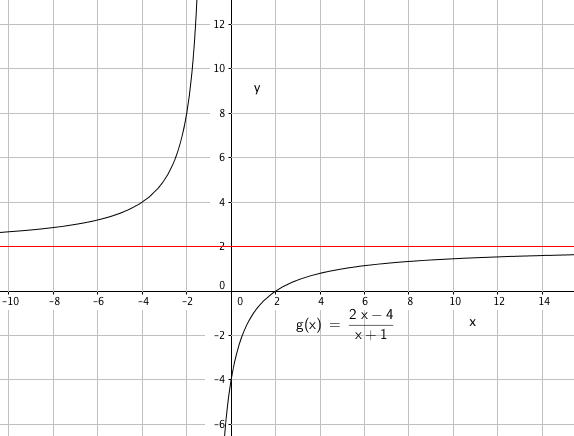
Vertikal asymptote for x= - 1 gir c = 1
Skjærer y akse i y = -4 gir g(0) = -4 som gir b = -4
Skjærer x aksen i x = 2 gir g(2) = 0 eller $2 \cdot 2 - 4 = 0$ som gir a=2
Funksjonsuttrykket blir da:
$g(x)= \frac{2x-4}{x+1}$
b)
Vertikal asymptote for x= -1
Horisontal asymptote finner vi ved å dele alle ledd i teller og nevner på x, for så å la x gå mot uendelig. Man ser at g går da mot 2. Atså er horisontal asymptote y = 2.
Oppgave 8
a)
Gjennomsnittlig vekstfart i intervallet null til hundre:
$\frac{\Delta y}{\Delta x} = \frac{(1000 +3000 +1000) - 1000}{100} = 40$
Den gjennomsnittlige vekstfarten i intervallet er 40. Det betyr at kostnadene ved å produsere en enhet mere øker med 40.
b)
$K´(x)= 0,2x+30 \\ K´(100) = 50$
Det forteller oss at kostnaden ved å øke produksjonen med en enhet er ca. 50.
c)
Oppgave 9
a)
Nullpunkt:
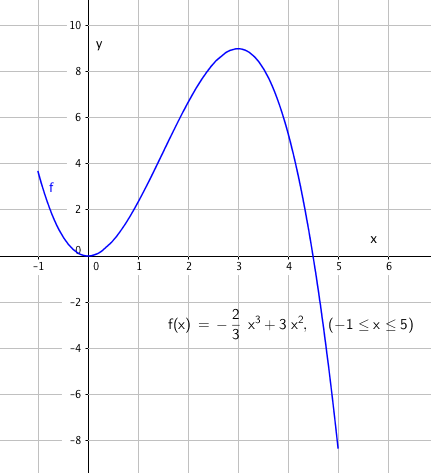
$f(x)=0 \\ - \frac 23 x^3 + 3x^2 =0 \\ x^2( - \frac23 x+3)= 0 \\ x = 0 \vee x = \frac 92$
Nullpunkter: $(0,0) \wedge ( \frac 92 , 0)$
b)
Ekstremalpunkter:
$f´(x)= -2x^2+6x \\ f´(x)=0 \\ -2x^2+6x=0 \\ x(-2x+6)=0 \\ x=0 \vee x=3$
f´(-1) er negativ. f´(1) er positiv. f´(4) er negativ.
Det gir munimum for x= 0 og maksimum for x = 3.
Min: (0, f(0)) = (0, 0)
Maks: (3, f(3)) = (3, 9)
c)
d)
$f´(x)=-2x^2+6x \\ f´(1) = -2+6 =4 \\ f(1)= - \frac 23 + 3 = \frac 73$
$y =ax+b \\ y=4x+b \\ \frac73= 4 \cdot 1 + b \Rightarrow b= - \frac53$
Likningen til tangenten blir da: $y=4x - \frac 53$
DEL TO
Oppgave 1
a)
b)
c)
Oppgave 2
a)
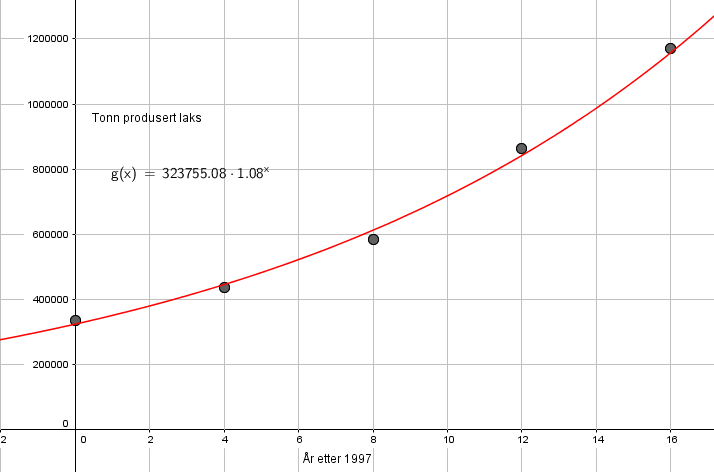
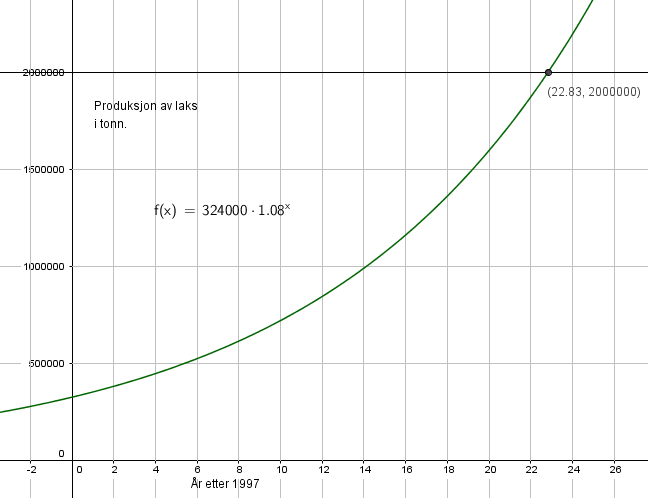
Vekstfaktoren er 1,08, det betyr at det er en økning på 8% per år.
b)
Produksjonen passerer 2000000 tonn i år 2000.
c)
Oppgave 3
a)
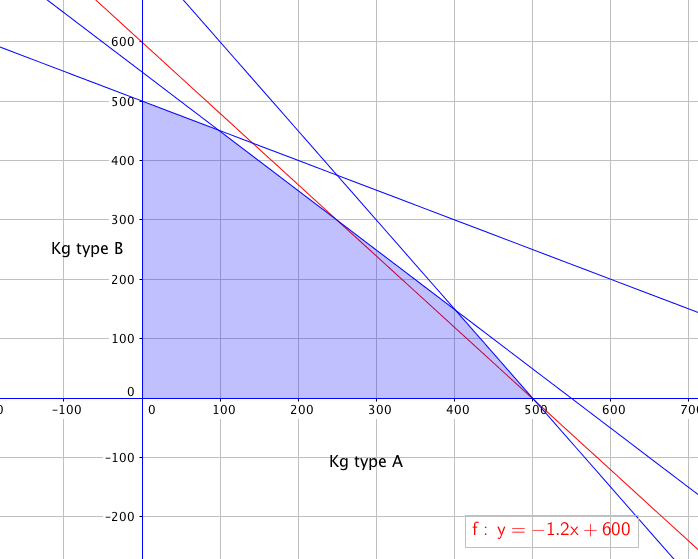
x er kilogram type A y er kilogram type B
$x \geq 0 \\ y \geq 0$
Produksjonen må være et positivt antall kg.
$x+y \leq 550$
De greier ikke selge mere enn 550 kg totalt.
$0,6x+0,4y \leq 300$
Er berensningen i tilgang på torsk.
$0,2x+0,4y \leq 200$
Er begrensningen i tilgang på sei.
b)
c)
Variable kostnader per kg, type A: $0,6 \cdot 55kr + 0,2 \cdot 35kr = 40 kr$
Variable kostnader per kg, type B: $0,4 \cdot 55 kr + 0,4 \cdot 35kr = 36 kr$
Fortjeneste: $(70-40)x+ 61-36)y 5000 = 30x+25y-5000$
d)
Produksjonene er begrenset av de blå linjene og må ligge i det skraverte feltet i b. En rød nivålinje er lagt inn:
30x + 25y - 5000 = 10000
y= -1,2x+600
Vi observerer at fortjenesten kan bli noe større enn det, nærmere bestemt det volumet som er gitt i skjæringspunktet mellom linjene som begrenses av maksimumsalg og tilgang på
Oppgave 4
a)
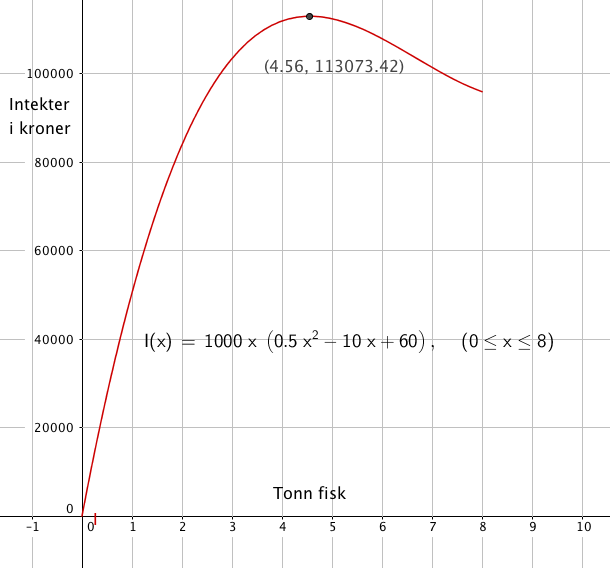
P(x) er kroner per kilogram. x er antall tonn. Inntektene blir antall kilo solgt multiplisert met kilopris:
$I (x) = 1000 \cdot x \cdot P(x)$
b)
Salg av ca 4,5 tonn fisk gir de største inntektene, ca 113 000 kroner per uke.