DEL 1

Oppgave 1

1, 5, 1, 3, 3, 1, 4, 2, 4, 0

I stigende rekkefølge:

0, 1, 1, 1, 2, 3, 3, 4, 4, 5

Medianverdi blir gjennomsnittet av tall fem og seks, altså: $\frac{2 + 3}{2} = 2, 5$

Typetall: 1 (den verdi det er mest av)

Gjennomsnitt, Summen av verdier, delt på antall verdier. $\frac{0 + 1 + 1 + 1 + 2 + 3 + 3 + 4 + 4 + 5}{10} = \frac{24}{10} = 2, 4$

Variasjonsbredde er største verdi minus minste verdi: 5 - 0 = 5.

Oppgave 2

Dersom 5% tilsvarer 40 kroner er 1% $\frac{40}{5} = 8$ kr. Varen kostet $100 \cdot 8 k r = 800 k r .$ før den ble satt opp.

Oppgave 3

Kaffe i norge: 1 920 000 liter

Kopp: 1,5 desiliter

1 920 000 l = 19 200 000 dl = $1, 92 \cdot 10^{7}$

Deler totalvolumet på volumet av en kopp:

Det drikkes $\frac{1, 92 \cdot 10^{7}}{1, 5} = 1, 28 \cdot 10^{7}$ kopper kaffe i Norge daglig.

Oppgave 4

$3^{3} \cdot \frac{1}{9} - 2^{3} (4 - 1) = 27 \cdot \frac{1}{9} - 8 \cdot 3 = 3 - 24 = - 21$

Oppgave 5

a)

I kamp nr. 4 scoret hun 21 - 15 = 6 mål.

b)

På 6 kamper scoret hun totalt 30 mål. Det blir i snitt $\frac{30}{6} = 5$ mål per kamp.

Oppgave 6

a)

For å finne en tilnærmet verdi for gjennomsnittet i klassedelt materiale må vi anta at verdiene fordeler seg jevnt i hver klasse.

Vi multipliserer klassemidtpunktene med frekvensene, summerer og dividerer på det totale antall, som i dette tilfelle er 14:

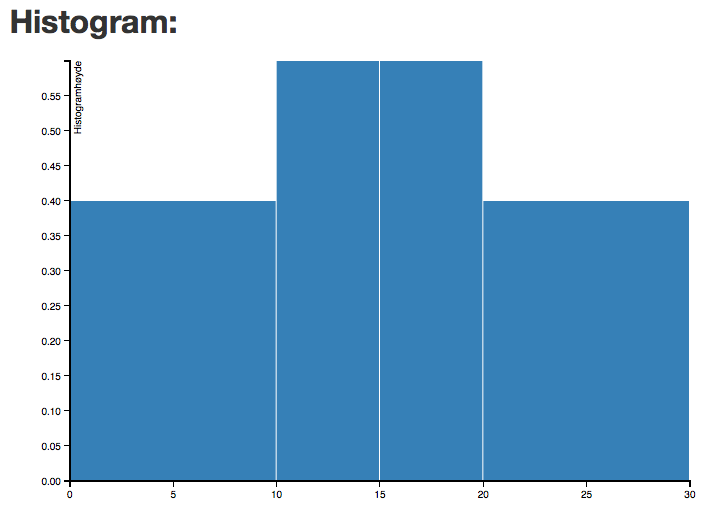
$5 \cdot 4 = 20 12, 5 \cdot 3 = 37, 5 17, 5 \cdot 3 = 52, 5 25 \cdot 4 = 100 20 + 37, 5 + 52, 5 + 100 = 210 210 : 14 = 15$

b)

$H i s t o g r a m h ø y d e = \frac{F r e k v e n s}{K l a s s e b r e d d e}$

Husk at det er arealet av "søylene" som er viktig. Høyde gange bredde gir frekvensen i hver enkelt klasse.

Oppgave 7

a)

Dersom man løper med 10 km/h bruker man $\frac{1}{10}$ time på 1 km. 1/10 time tilsvar 6 min, siden det er 60 min i en time.

b)

$\frac{1}{12}$ time gir 5 min på en km.

c)

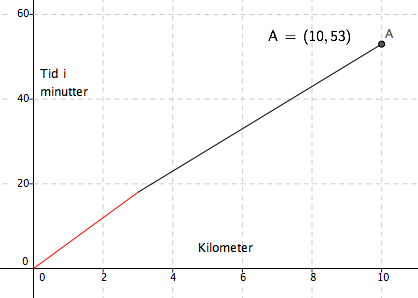
d)

Hun bruker 53 min på 10 km. altså brukte hun i snitt 5,3 min per km, eller 5 min og 18 sekunder.

Oppgave 8

a)

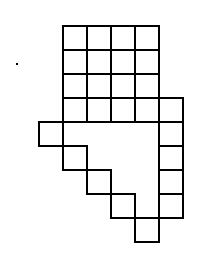
Figur 4.

b)

Små kvadrater i figur fem:

I denne type oppgave ser jeg alltid etter systemer. Vi ser at alle figurene har et kvadrat der sidekantene tilsvarer figurnummer i antall små kvadrater. Det blir 5 gange 5 som er 25. I tillegg har figuren to rader med små kvadrater som begge har ett mere enn figurtallet, altså 6 +6 = 12.

25 + 12 = 37 små kvadrater i figur 5.

c)

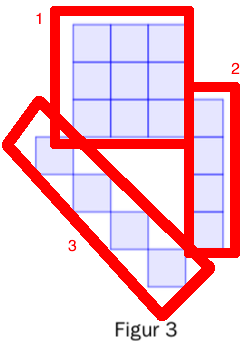
Vi tar utgangspunkt i figur nr. 3. Vi ser at vi kan dele alle figurene inn i tre områder, 1, 2 og 3. Fordi vi har figur nr.3 prøver vi nå å uttrykke antall små kvadrater med 3. Vi ser at:

Område 1: $3 \cdot 3$

Område 2: 3 + 1

Område 3: 3 + 1

For å finne et uttrykk for figur n, erstatter vi alle 3 tall med n og legger sammen:

$(n \cdot n) + (n + 1) + (n + 1) = n^{2} + 2 n + 2$

Vi kan døpe utrykket over til A, antall som funksjon av n og får:

$A (n) = n^{2} + 2 n + 2$

d)

$A (n) = n^{2} + 2 n + 2 A (100) = 100^{2} + 2 \cdot 100 + 2 A (100) = 10000 + 200 + 2 A (100) = 10202$

2PY 2018 høst LØSNING