DEL EN

Oppgave 1

a)

$3^{x - 5} = 81 3^{x - 5} = 3^{4} x - 5 = 4 x = 9$

b)

$x^{2} - 7 x + 10 = 0$

Faktoriserer

$x^{2} - 7 x + 10 = (x - 2) (x - 5)$

Finner nullpunktene:

$(x - 2) (x - 5) = 0 x = 2 \lor x = 5$

Kan også bruke abc - formelen for faktorisering.

c)

$l g (x + 3) - l g x = 1 x > 0 l g (\frac{x + 3}{x}) = 1 10^{l g (\frac{x + 3}{x})} = 10^{1} \frac{x + 3}{x} = 10 x + 3 = 10 x 9 x = 3 x = \frac{1}{3}$

Oppgave 2

a)

$\frac{16^{2} \cdot 27^{3}}{72^{2} \cdot 12} = \frac{(2^{4})^{2} \cdot (3^{3})^{3}}{(2^{3} \cdot 3^{2})^{2} \cdot 2^{2} \cdot 3} = \frac{2^{8} \cdot 3^{9}}{2^{6} \cdot 3^{4} \cdot 2^{2} \cdot 3} = \frac{2^{8} \cdot 3^{9}}{2^{8} \cdot 3^{5}} = 2^{8 - 8} \cdot 3^{9 - 5} = 2^{0} \cdot 3^{4} = 3^{4} = 81$

b)

$\frac{x - 2}{x - 1} - \frac{x}{x + 1} - \frac{2 x}{x^{2} - 1} = \frac{(x - 2) \cdot (x + 1)}{(x - 1) \cdot (x + 1)} - \frac{x \cdot (x - 1)}{(x + 1) \cdot (x - 1)} - \frac{2 x}{(x + 1) (x - 1)} = \frac{(x^{2} + x - 2 x - 2) - (x^{2} - x) - 2 x}{(x - 1) (x + 1)} = \frac{x^{2} + x - 2 x - 2 - x^{2} + x - 2 x}{(x - 1) (x + 1)} = \frac{- 2 x - 2}{(x - 1) (x + 1)} = \frac{- 2 (x + 1)}{(x - 1) (x + 1)} = - \frac{2}{x - 1}$

c)

$l g (\frac{2}{x^{2}}) + l g (2 x^{2}) + l g (x) - l g (4 x) = (l g (2) - l g (x^{2})) + (l g (2) + l g (x^{2})) + l g (x) - (l g (4) + l g (x)) = l g (2) - 2 l g (x) + l g (2) + 2 l g (x) + l g (x) - l g (2^{2}) - l g (x) = 2 l g (2) + l g (x) - 2 l g (2) - l g (x) = 0$

Oppgave 3

$[\begin{array}{r} x^{2} + 2 y = 13 x \\ 3 x - y = - 5 \end{array}]$

Løser andre likning og setter inn i den første.

$y = 3 x + 5$

Vi setter inn for y i den første likningen:

$x^{2} + 2 (3 x + 5) = 13 x x^{2} + 6 x + 10 = 13 x x^{2} - 7 x + 10 = 0$

Fra oppgave 1b) har vi at $x_{1} = 2$ og $x_{2} = 5$

Fra andre likning har vi:

$y_{1} = 3 \cdot 2 + 5 = 11$

$y_{2} = 3 \cdot 5 + 5 = 20$

Løsning: $x_{1} = 2$ , $y_{1} = 11$ og $x_{2} = 5$ , $y_{2} = 20$

Oppgave 4

a)

Pris brus = x og pris pølse = y.

$[\begin{array}{r} 6 x + 4 y = 170 \\ 5 x + 10 y = 275 \end{array}]$

b)

Løser likning II med hensyn på x:

$5 x = 275 - 10 y x = 55 - 2 y$

setter så uttrykket for x inn i likning I:

$6 (55 - 2 y) + 4 y = 170 330 - 12 y + 4 y = 170 - 8 y = - 160 y = 20$

Setter inn y=20 i likning II:

$x = 55 - 2 \cdot 20 = 55 - 40 = 15$

En brus koster 15 kroner og en pølse koster 20 kroner.

Oppgave 5

a)

$f (x) = x^{3} + 3 x f^{'} (x) = 3 x^{2} + 3 f^{'} (1) = 3 \cdot 1 + 3 = 6$

Når x =1 har funksjonen en momentan vekstfart på 6.

b)

Den deriverte er positiv for alle verdier av x, derfor er funksjonen voksende og har kun positive tangenter.

c)

$f^{'} (x) = 15 3 x^{2} + 3 = 15 3 x^{2} = 12 x^{2} = 4 x = \pm 2$

Oppgave 6

a)

$(\binom{10}{3}) = \frac{10 \cdot 9 \cdot 8}{3 \cdot 2 \cdot 1} = 10 \cdot 3 \cdot 4 = 120$

120 ulike grupper på tre deltakere kan komme til finalen.

b)

Vi har flere kvinner enn menn i en gruppe på tre, dersom vi har to eller tre kvinner.

P(to eller tre kvinner) = $\frac{(\binom{5}{2}) (\binom{5}{1})}{(\binom{10}{3})} + \frac{(\binom{5}{3}) (\binom{5}{0})}{(\binom{10}{3})} = \frac{10 \cdot 5}{120} + \frac{10 \cdot 1}{120} = \frac{60}{120} = \frac{1}{2}$

60 av de 120 gruppene, det vil si halvparten, inneholder flere kvinner enn menn.

Oppgave 7

a)

Ulikhetene som begrenser området:

$x \geq 0$

$y \geq 0$

$y \leq 0, 5 x + 2$

$y \leq - 2 x + 6$

b)

Finner skjæringspunktene for de to linjene:

$0, 5 x + 2 = - 2 x + 6 2, 5 x = 4 x = \frac{4}{2, 5} = \frac{16}{10} = 1, 6$

$y = 0, 5 \cdot 1, 6 + 2 = 0, 8 + 2 = 2, 8$

Sjekker hjørnene i område for den største verdien av $3 x + y$

$(1.6, 2.8) \Rightarrow 3 \cdot 1.6 + 2.8 = 4.8 + 2.8 = 7.6$

$(0, 2) \Rightarrow 3 \cdot 0 + 2 = 2$

$(3, 0) \Rightarrow 3 \cdot 3 + 0 = 9$

Den største verdien størrelsen $3 x + y$ kan ha innenfor det blå området er 9..

c)

$(0, 2)$ satt inn i størrelsen $y - a \cdot x$ gir verdien $2 - a \cdot 0 = 2$

Verdien av $a$ må være slik at de andre to hjørnene ikke får en verdi større enn 2.

For hjørnet $(3, 0)$ får vi verdien $0 - a \cdot 3 = - 3 a$ . Vi har $- 3 a < 2$ for alle $a > - \frac{2}{3}$

For hjørnet $(1.6, 2.8)$ får vi verdien $2.8 - a \cdot 1.6$ .

$2.8 - a \cdot 1.6 < 2 - 1.6 a < - 0.8 a > 0, 5$

Vi må ha $a > 0, 5$ for at størrelsen $y - a \cdot x$ skal ha størst verdi i $(0, 2)$ .

Oppgave 8

a)

Omkrets: $O = 4 y + 8 x = 12 4 y = 12 - 8 x y = 3 - 2 x$

Areal: $A = y^{2} + 2 x^{2} A (x) = (3 - 2 x)^{2} + 2 x^{2} A (x) = 9 - 12 x + 4 x^{2} + 2 x^{2} A (x) = 6 x^{2} - 12 x + 9$

b)

$A^{'} (x) = 12 x - 12 A^{'} (x) = 0 12 x - 12 = 0 x = 1$

Innsatt for y: $y = 3 - 2 x y = 3 - 2 \cdot 1 y = 1$

Det minste arealet får man når både x = 1 og y = 1.

DEL TO

Oppgave 1

a)

Vi har $x \geq 0$ og $y \geq 0$ fordi bakeren må lage 0 eller flere kaker. Han kan ikke lage et negativt antall kaker.

La x være antall kaker av type A, og y være antall kaker av type B.

For mel har vi:

$300 x + 500 y \leq 50000 \frac{300}{100} x + \frac{500}{100} y \leq \frac{50000}{100} 3 x + 5 y \leq 500$

For sukker har vi:

$100 x + 50 y \leq 7000 \frac{100}{50} x + \frac{50}{50} y \leq \frac{7000}{50} 2 x + y \leq 140$

For smør har vi:

$125 x + 50 y \leq 8500 \frac{125}{25} x + \frac{50}{25} y \leq \frac{8500}{25} 5 x + 2 y \leq 340$

b)

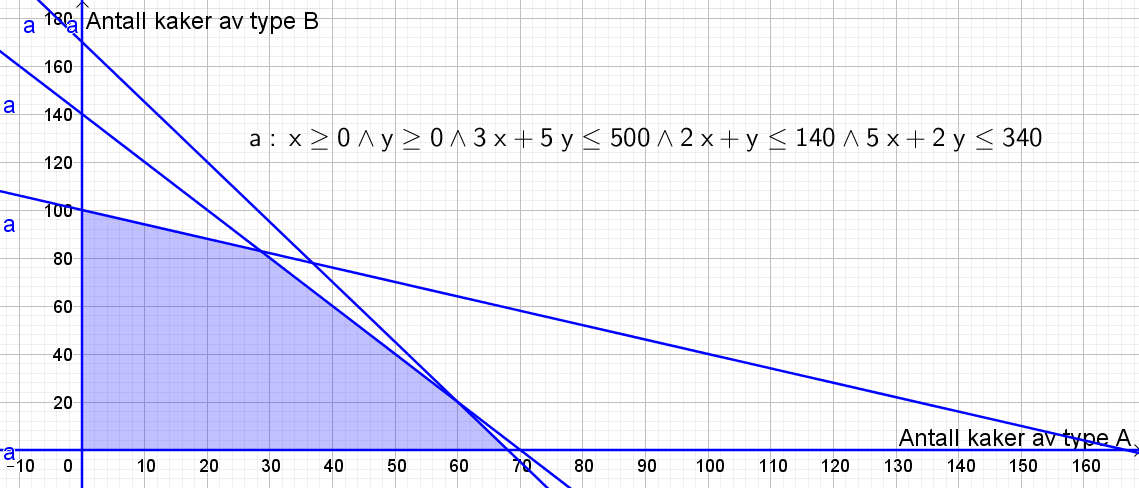
Bruker Geogebra og legger inn ulikhetene.

c)

Fortjenesten er gitt ved: $I (x, y) = 160 x + 120 y$

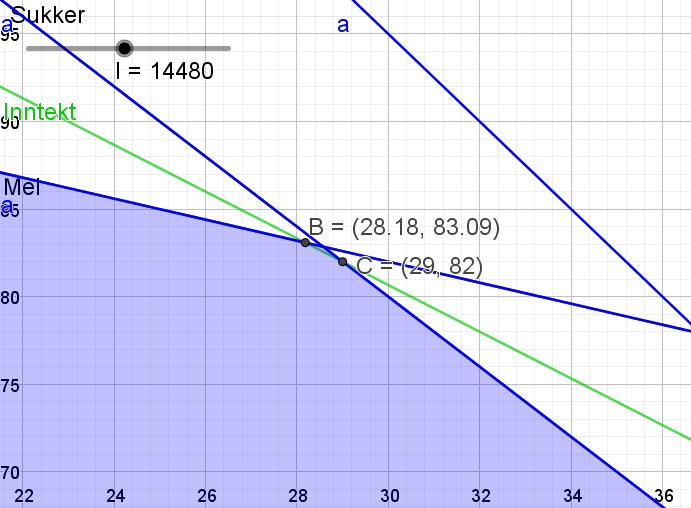
Legger inn en glider for fortjenesten i Geogebra. Lager "skjæring mellom to objekt" mellom linjen $3 x + 5 y = 500$ og glideren (gir punkt B), samt mellom linjen $2 x + y = 140$ og glideren (gir punkt C). Ved hjelp av glideren finner jeg antall hele kaker som gir maksimal fortjeneste.

Bakermester Snipp må bake 29 kaker av type A og 82 kaker av type B. Fortjenesten blir da $160 \cdot 29 + 120 \cdot 82 = 14480$ kr.

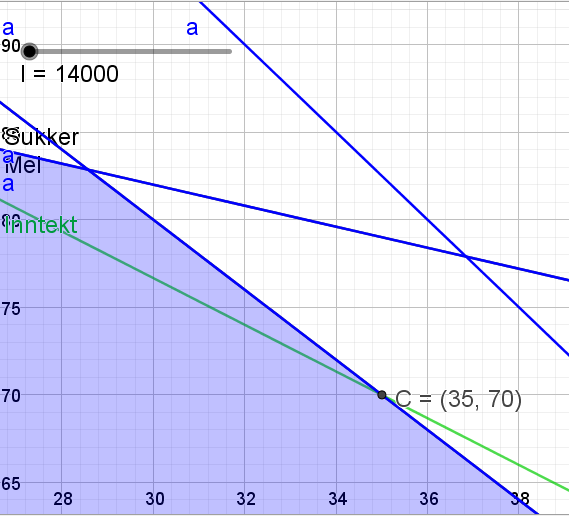
d)

Bruker glideren fra oppgave c) og beveger den ned til punktet C=(35,70), der hvor det lages 70 kaker av type B. Fortjenesten blir da $160 \cdot 35 + 120 \cdot 70 = 14000$ kr.

S1 2019 vår LØSNING

DEL EN

Oppgave 1

a)

b)

c)

Oppgave 2

a)

b)

c)

Oppgave 3

Oppgave 4

a)

b)

Oppgave 5

a)

b)

c)

Oppgave 6

a)

b)

Oppgave 7

a)

b)

c)

Oppgave 8

a)

b)

DEL TO

Oppgave 1

a)

b)

c)

d)

Oppgave 2

a)

Innholdto top