Løsning-Eksempelsett-2P-300821

DEL EN

Oppgave 1

Ett parti øker oppsluttningen fra 5% til 7%. Det er en $\frac{2}{5}= \frac{4}{10} = 40$ % økning.

Oppgave 2

Programmet regner ut hvor lang tid det tar før verdien til en vare er halvert, når verdien avtar med 15% per år. Linje 10 skriver ut denne verdien og linje 11 skriver ut hvor lang tid det tar.

Oppgave 3

Dersom et produkt skal bli null, må en eller flere av faktorene være null.

Løsning: x = 0 eller x = 3 eller x = -1.

Oppgave 4

Vi kan finne høyden i trekanten ved å bruke Pytagoras. Den blir 8 cm. Normalen på AB gjennom C deler AB i to like store biter, fordi trekanten er likebeint. Vi finner da arealet av den rettvinklede trekanten som er halvparten av trekant ABC.

Arealet av trekanten blir da grunnlinje gange høyde delt på to, som er $24 cm^2$. Da har vi funnet arealet av halvparten av trekanten. Arealet av trekanten ABC blir da $A= 48 cm^2$

Oppgave 5

Det er høyden på arket som begrenser størrelsen på bildet. Vi bruker formlikhet:

$\frac{8}{28} = \frac{x}{42}$

$x= \frac{8 \cdot 42}{28} =12$

Bildet kan bli 42 cm høyt. Da blir det 12 cm i bredden.

Oppgave 6

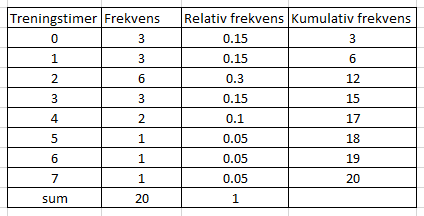
Vi kan bruke 2 treningstimer som eksempel. Frekvensen er 6. Den relative frekvensen forteller hvor mange timer 6 er av 20, altså 6/20 som er 0,3 eller 30%. Den kumulative frekvensen for 2 treningstimer er 12. Det betyr at 12 personer trene 2 timer eller mindre (3 + 3 + 6).

Oppgave 7

I et histogram representerer arealet av en enkelt søyle antallet eller frekvensen. Antallet elever som er under 180 cm høye blir summen av arealene som er under 180cm: 10 + 30 + 50 = 90 elever.

Oppgave 8

Begrunnelsen i oppgaven er riktig. $4x^2-2x+5$ er en "smilende" parabel som ligger over x- aksen. Ulikheten har derfor ingen løsning.

DEL TO

Oppgave 1

Synne har rett. Når noe minker med 4% er vekstfaktoren 0,96.

Thea, ja man kan bruke den vekstfaktoren. Siden verdien minker var den større for åtte år siden, enn i dag, så det har Thea rett i.

Dersom vi kaller båtens verdi for ått år siden for x får vi:

$x \cdot 0,96^{8} = 45000$

$x = 45000 \cdot 0,96^{-8}$

x= 62400

For åtte år siden var båtens verdi rundt 62 000 kroner. (ikke noe poeng å regne på krona her, dette er også en modell for verdiutviklingen og svaret er ikke eksakt uansett antall desimaler).

Oppgave 3

a)