1T 2021 høst LK20 LØSNING

Diskusjon av denne oppgaven på matteprat

DEL 1

Oppgave 1

Vet at stigningstallet for begge linjene er det samme, nemlig -2, siden linjene er parallelle.

Bruker ettpunktsformelen, hvor $x_1=5,y_1=-6,a=-2$

$y-y_1=a(x-x_1)$

$y-(-6)=-2(x-5)$

$y+6=-2x+10$

$y=-2x+10-6$

$y=-2x+4$ er likningen for linjen m.

Oppgave 2

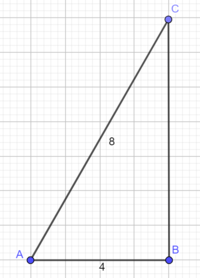
Tegner en hjelpetrekant.

Vet at $cosA=sinA=\frac{AB}{AC}=\frac{1}{2}$ og siden $AB=4$, har vi $AC=8$

Oppgave 3

Skal løse likningen $x^3+2x^2-7x+4=0$

Ser at x=1 er en løsning til likningen. Sjekker at det stemmer:

$1^3+2\cdot 1^2-7\cdot 1+4=1+2-7+4=0$

Det stemmer at x=1 er en løsning, og dermed er (x-1) en faktor. Bruker polynomdivisjon for å faktorisere resten av uttrykket.

$(x^3+2x^2-7x+4):(x-1)=x^2+3x-4$

$-(x^3-x^2)$

_____________________________

$3x^2-7x+4$

$-(3x^2-3x)$

_____________________________

$-4x+4$

$-(-4x+4)$

_____________________________

$0$

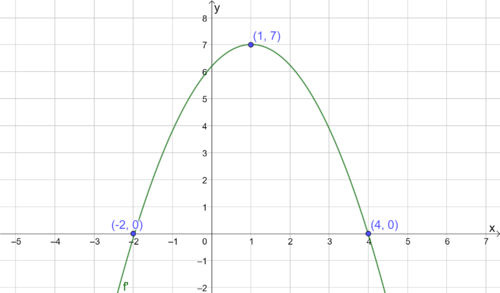
Faktoriserer $x^2+3x-4=(x+4)(x-1)$

Faktoriserer hele uttrykket $x^3+2x^2-7x+4=(x+4)(x-1)(x-1)$

Tredjegradslikningen har to løsninger: $x=-4$ og $x=1$

Oppgave 4

Fra likning II har vi at $y=-2-x$

Setter dette inn i likning I:

$x^2+2x-(-2-x)=-1$

$x^2+2x+2+x=-1$

$x^2+3x+3=0$

Bruker andregradsformelen:

$x=\frac{-3\pm \sqrt{3^2-4\cdot 1\cdot 3}}{2\cdot 1}$

$x=\frac{-3\pm \sqrt{-3}}{2}$

Vi får et negativt tall under kvadratroten, så denne likningen har ingen løsning. Derfor har heller ikke likningssystemet noen løsning.

Oppgave 5

DEL 2

Oppgave 1

a)

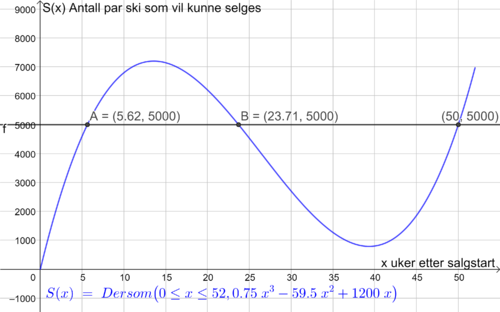
Tegner grafen til funksjonen S i Geogebra. Lager linja y=5000 og finner skjæringspunktene mellom linja og grafen til S. Ser at butikken kan selge mer enn 5000 par ski fra uke 5.6 til uke 23.7 (litt over 18 uker), og fra uke 50 til 52 (2 uker). Det vil si at butikken kan selge mer enn 5000 par ski i ca. 20 uker, ifølge modellen.