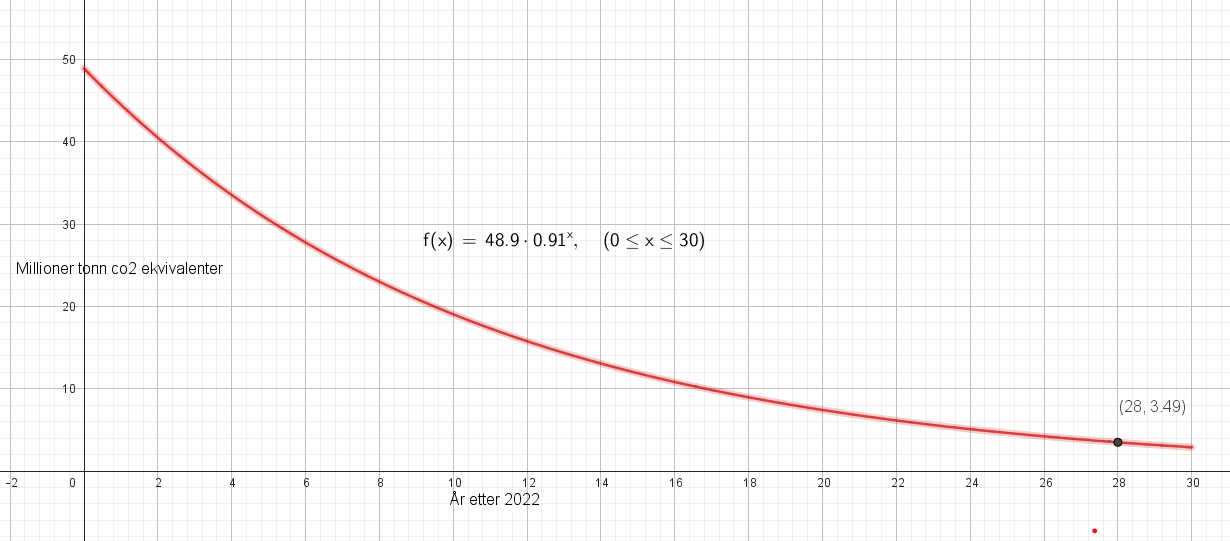
2P 2023 Høst LØSNING
Diskusjon av oppgaven på matteprat
MAT 1023
DEL EN
Oppgave 1
a)
$415:25= 16,6$ Dvs. man må reise 17 ganger eller mer for at det skal lønne seg.
b)
$\frac{85 \cdot 100}{500} = \frac{85}{5} = 17$ %
Hun sparer 17% på å kjøpe et flexikort.
Oppgave 2
$\frac{40 cm}{2000000 cm} = \frac{4 cm}{200000 cm} = \frac{1}{50000}$
Målestokken er 1: 50 000.
Oppgave 3
Alternativ 1:
Siden median er 8 og typetall 5 tenker jeg
5, 5, 5, 5, 8, 8 .........
Jeg vet at gjennomsnittet skal bli 9 km. på 10 gager blir det 90 km. Jeg mangler 90 - ( 5+5+5+5+8+8) = 54. En mulig løsning blir da:
5, 5, 5, 5, 8, 8, 13, 13, 14, 14
Alternativ 2:
Jeg velger å ta med kun to femmere og tenker at jeg prøver med følgende:
4, 5, 5, 6, 7, 9,...........
Medianverdien vil nå bli 8, selv om jeg ikke bruker 8. Typetallet er 5. Summen skal fortsatt være 90: Plukker ut tall jeg ikke brukte i alternativ 1.
4, 5, 5, 6, 7, 9, 10, 11, 12, 21
Alle krav oppfylt.
Oppgave 4
Dersom man multipliserer (ganger) to tall med hverandre må mist ett av tallene være null, for at produktet skal bli null. Slik er det alltid.
Det som blir sagt om den andre likningen er feil.
$(x+2)(x-3) = -6$
$x^2-3x+2x-6 +6 =0$
$x^2-x = 0$
$x( x-1) =0$
Her ser man at x=0 eller x=1 er løsninger av likningen.
DEL TO
Oppgave 1
x er prisen på en vase, og y er prisen på en rose.
Rosen koster 12 kroner og en vase koster 225 kroner.
Oppgave 2
Prisøkning ett spesielt merke sjokoladepålegg 2019 - 2022: $ \frac{39,90}{35,90} = 1,111$, altså en økning på 11,1%
Prisindeks sjokoladepålegg samme periode: $ \frac{119,8}{99,9} = 1,199$, som er en økning på 19,9%
Det bestemte merket har hatt en økning lavere enn prisindeksen.
Oppgave 3
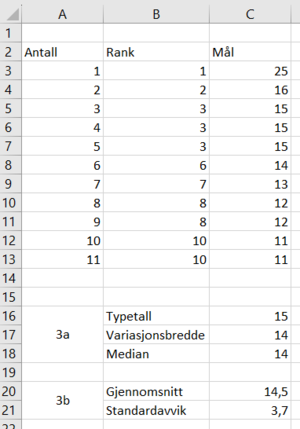
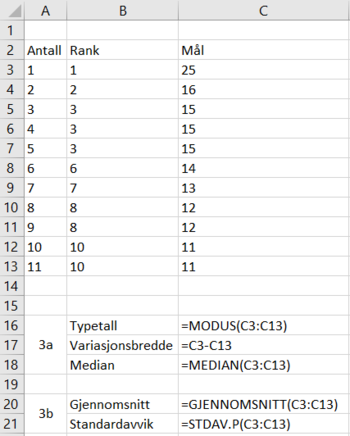
a)
b)
Se opg. a.
c)
I 2021 var spredningen større, Det var større forskjell på antall skårte mål. I 2021 ser det ut som en liten gruppe spillere drar opp snittet (altså skårte mange mål), siden gjennomsnittet er likt de to årene, mens median er 3 mål lavere i 2021.
Oppgave 4
Oppgave 5
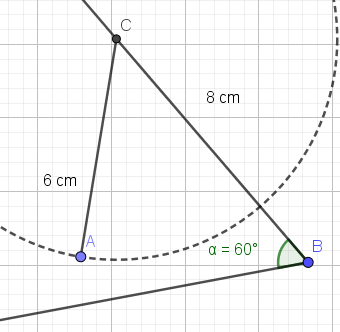
Denne oppgaven lar seg ikke løse fordi det ikke er mulig å danne en trekant med de oppgitte verdier. Det var nok meningen at vi skulle få en spissvinklet og en stompvinklet trekant ut fra samme data, men et sted på veien ble enten vinkel B for stor, BC for lang eller AC for kort...
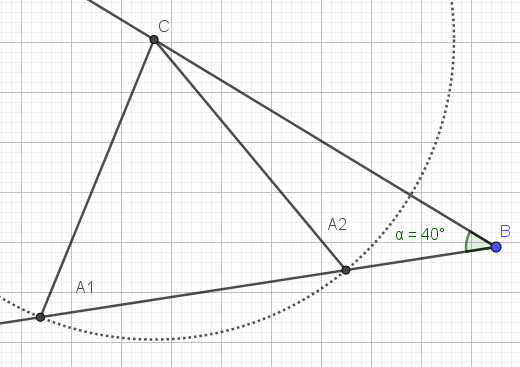
Vel, riktig svar er at ingen av elevene har rett. Men, dersom man reduserer vinkel B til for eksempel 40 grader kan "UDIR's trekant" se slik ut.
Vi vil vel anta at dette er en feil fra UDIR's side og at oppgaven blir strøket. Man bør kanskje også vurdere å gi kandidatene en ytterligere kompensasjon pga unødvendig bruk av tid ol., men det er jo opp til UDIR å avgjøre.
Oppgave 6
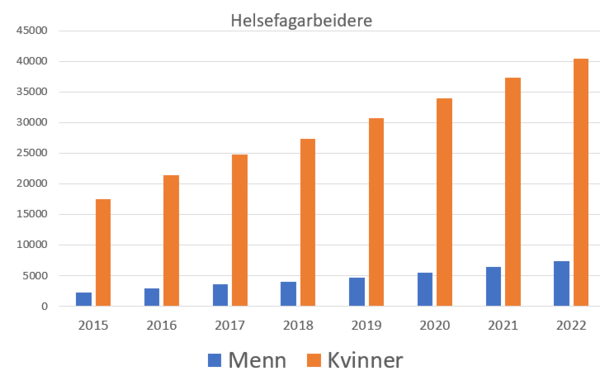
Figuren over er et relativt sannferdig diagram av hvordan det står til med antall helsefagarbeidere i forholdt til antall og kjønn over de sisste årene.
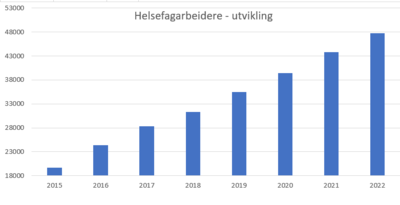
Dersom jeg var politiker og ville skryte av min formidable innsats i helsessektoren ville jeg vurdert søylediagrammet nedenfor. Legg merke til starten på y aksen. Dette er en vanlig måte å bruke statistikk til å gi et feilaktig inntrykk av situasjonen.
Hvordan er det egentlig med andelen menn? Begge figurene bruker samme tallmaterialet, men den til venstre er vel mest optimistisk og viser en tydelig vekst i antall menn i yrket. Søylediagrammet til høyre viser et mer realistisk bilde av situasjonen,
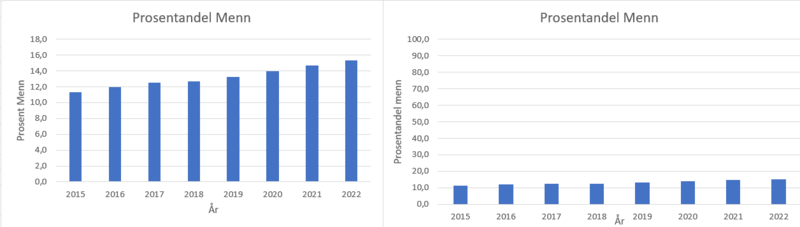
Nedenfor ser du grunnlaget for diagrammene.
Problemet med oppgaver av denne typen at man vet aldri helt når det er nok. Dersom oppgavene hadde en poengsum (som før) kunne man vurdere vektingen i forhold til andre oppgaver. Da ville jo arbeidsmengdene stå i forhold. Men, vi tenker dette er nok på denne oppgave selv om vi kun bruker søylediagram.
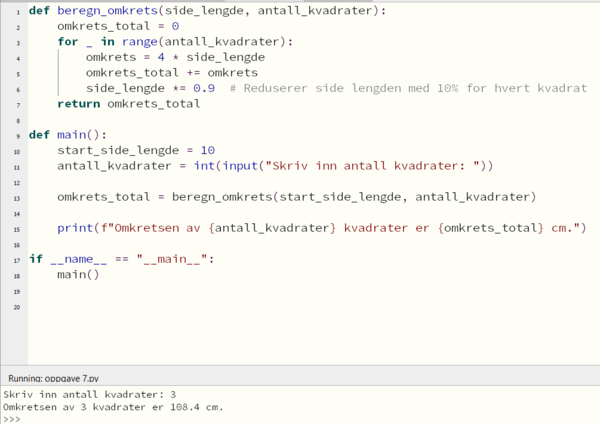
Oppgave 7
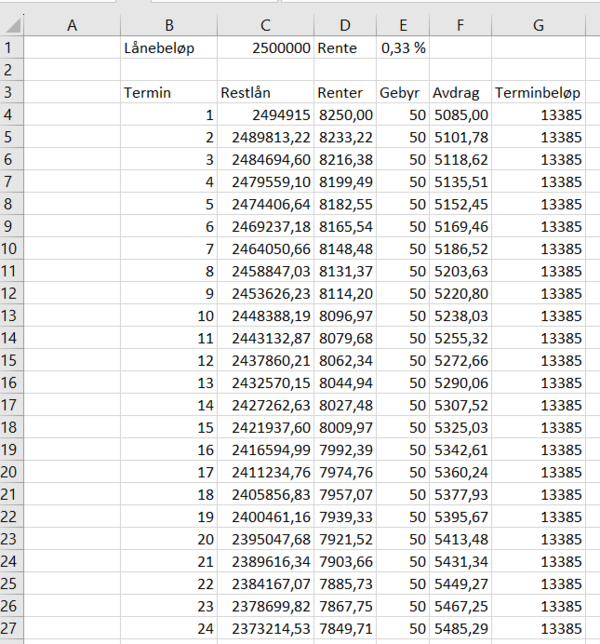
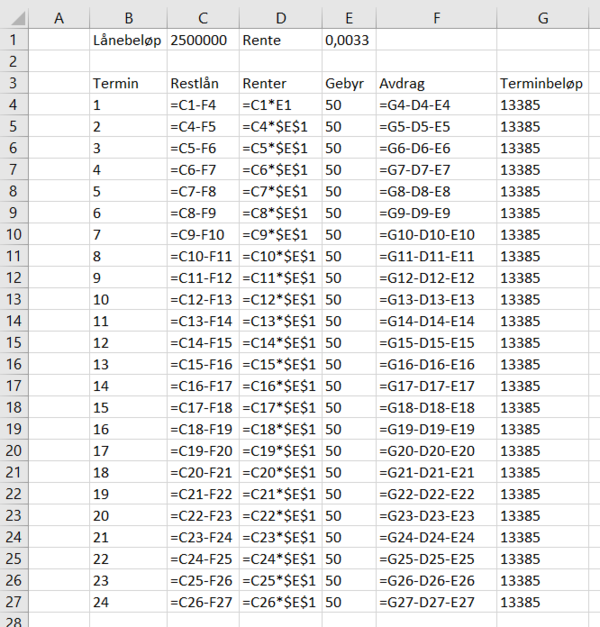
a)
b)
Se figur i opg. a.
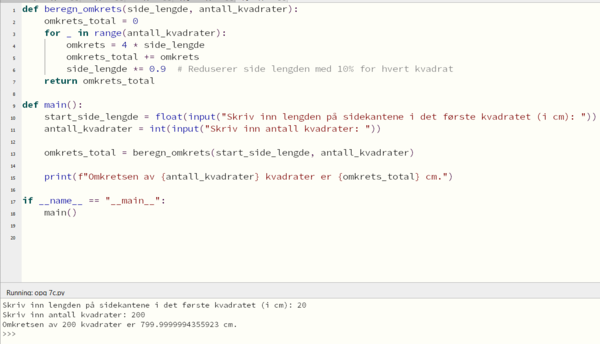
c)
Når sidekanten er 10 cm går summen av omkretsene mot 400 cm, og når sidekantene er 20 cm til å begynne med går summen av omkretsene mot 800 cm.
Mer generelt : T = 4 * s * 10
Der T er summen av omkretsen av alle kvadratene *og s er lengden av en sidekant i det første kvadratet.
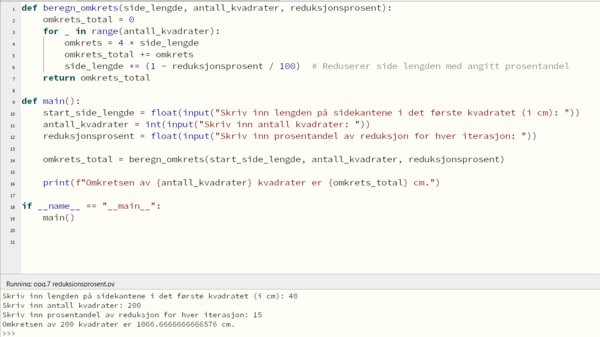
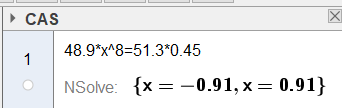
d)
Ja, ingen bevis, men testing på programmet tilsier at det er riktig.
Oppgave 8
a)