R1 2012 vår LØSNING
Andre løsninger
Noen oppgaver løst som videoer fra UDL.no
DEL EN
Oppgave 1:
a)
1)
<math>f(x) = 5x^3+x-4 \\ f'(x) = 3 \cdot 5x^2 + 1 \\ f'(x) = 15x^2 + 1 </math>
2)
<math>g(x) = 5e^{3x} \\ u = 3x \wedge u' = 3 \\ g'(x) = 5e^u \cdot u' \\ g'(x) = 15e^{3x}</math>
b)
<math> 2\ln(\frac{a^2}{b}) + \ln (a \cdot b) - 3\ln a = \\ 2\ln a^2 - 2\ln b + \ln a + \ln b - 3 \ln a = \\4\ln a - 2\ln b + \ln a + \ln b - 3 \ln a = \\ 2\ln a - \ln b </math>
c)
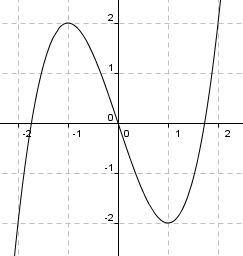
<math> f(x)= x^3-3x</math>
1)
Nullpunkter:
<math>x^3-3x = x(x^2-3)= x(x- \sqrt 3 )(x + \sqrt 3) \\x = - \sqrt3 \quad \vee \quad x = 0 \quad \vee \quad x= \sqrt3</math>
2)
<math>f'(x) = 3x^2-3 \\f'(x) = 0 \\ 3(x^2-1) = 0 \\ x = -1 \quad \vee \quad x = 1 \\ f(-1)= 2 \quad \vee \quad f(1) = -2</math>
Toppunkt (-1,2)
Bunnpunkt (1,-2)
3)
d)
<math>P(x) = x^3-3x^2-x+3 \\ P(3) = 27-27-3+3 =0 \\ \\ P(x):(x-3) \\ (x^3-3x^2-x+3): (x-3) =x^2-1
\\-(x^3-3x^2)\\ \quad \quad \quad \quad\quad \quad \quad -(-x+3) \\ \quad \quad \quad \quad\quad \quad \quad \quad\quad \quad \quad\quad \quad \quad 0</math>
Dette gir følgende løsninger:
x = - 1 eller x = 1 eller x = 3.
e)
<math>\vec r(t) = [3,0t ,-4,9t^2] \\ \vec v(t) = \vec r'(t) = [3,0 , -9,8t] \\ \vec a(t) = \vec v'(t) = \vec r(t) = [0 , -9,8] </math>
Oppgave 2:
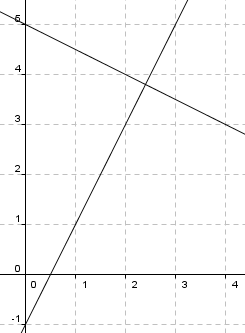
a)
b)
Skalarprodukt:
<math>[1,a_1]\cdot[1,a_2] = 0 \\ 1+ a_1 \cdot a_2 = 0 \\ a_1 \cdot a_2 =-1</math>
c)
<math>y= - \frac 12x+5</math>
d)
Oppgave 3:
a)
<math> f(x)= \frac1x \\ f'(x) = - \frac {1}{x^2} \\ f'(a) = - \frac {1}{a^2} \\ Rett \quad linje: \quad y=ax+b \\ y= - \frac{1}{a^2}x+ b </math>
Finner b ved å bruke punktet (a, f(a)):
<math>y = - \frac{1}{a^2}x+ b \\ \frac 1a = - \frac{1}{a^2}a+ b \\ b= \frac 2a </math>
Som gir likningen
<math>y = - \frac{1}{a^2}x+ \frac 2a</math>
b)
<math>y = - \frac{1}{a^2}x+ \frac 2a</math>
A:
<math> y=0 \\ 0 = - \frac{1}{a^2}x+ \frac 2a \\ \frac{x}{a^2} = \frac 2a \\ x=2a</math>
Koordinater A: (2a,0)
B:
<math> \frac 2a </math>
Koordinater B:<math>( \frac 2a, 0)</math>
c)
Arealet av trekanten avgrenset av tangenten og aksene er:
<math> A= \frac{2a \cdot \frac 2a}{2} = 2</math>
Man observerer at arealet er uavhengig av x.
DEL TO
Oppgave 4:
Oppgave 5:
<math> \vec{AB}=[2,-2]</math>
Lengde av radius:
<math>r= \frac 12 | \vec{AB}| = \frac 12 \sqrt8 = \sqrt2</math>
Sentrum S, av sirkel: <math>\vec{OS}= \vec{OA} + \frac 12 \vec{AB} = [2,4]+ \frac 12 [2,-2] = [3,3] </math>
Sentrum er i punktet (3,3). Et vilkårlig punkt på sirkelperiferien er (x,y). Vi får:
<math> (x-3)^2 + (y-3)^2 = (\sqrt 2)^2 \\ (x-3)^2 + (y-3)^2 =2 </math>
Oppgave 6:
a)
<math>\vec{EF} = [5,-5]</math>
Bruker [1, -1] som rettningsvektor. Parameterfremmstilling:
<math> l: \left [ x = 2 +t \\ y = 4-t \right]</math>
b)
Skjæring med x- akse: y = 0 gir t = 4 som gir x = 6. Skjæring i (6,0)
Skjæring med y- akse: x = 0 gir t = -2 som gir y = 6. skjæring i (0, 6)
c)
<math> [2+t-6, 4-t-3] \cdot [1,-1] =0 \\ [t-4, 1-t] \cdot [1,-1] =0 \\ t-4-1+t = 0 \\ t = \frac 52 \\ x = \frac 92 \wedge y = \frac 32</math>
Avstand mello G og l:
<math>\sqrt{( \frac{12}{2}- \frac{9}{2})^2 + (\frac{6}{2}- \frac{3}{2})^2} = \frac{3 \sqrt2}{2}</math>
Oppgave 7:
a)
<math>f(x) = \frac 52 e^{- \frac x2} \\ A = g(x) = \frac{f(x) \cdot x}{2} = \frac {\frac 52 e^{- \frac x2} \cdot x}{2} = \frac 54x e^{- \frac x2}</math>
b)
<math> g'(x)= \frac 54 e^{- \frac x2} + \frac 54 x e^{- \frac x2}\cdot( - \frac 12) = e^{- \frac x2}( \frac 54 - \frac{5x}{8}) \\ g'(x) = 0 \\ x = 2</math>
Inspeksjon viser at g har et maksimum for x=2.
<math>g(2)= \frac{5 \cdot 2}{4} e^{-1} = \frac{5}{2e}</math>
c)
Oppgave 8:
a)
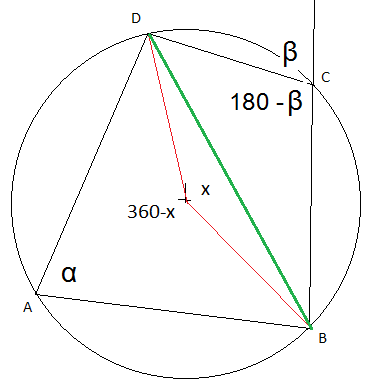
Når en periferivinkel og en sentralvinkel i en sirkel spenner over samme sirkelbue, så er periferivinkelen halvparten så stor som sentralvinkelen. En sentralvinkel har samme gradetall som sirkelbuen den spenner over.
Vinkelen alfa er periferivinkel og spenne over samme bue som sentralvinkelen x. Av det følger:
<math>\alpha = \frac x2</math>
b)
Periferivinkelen 180 grader minus beta, spenner over sirkelbuen DAB. Den sentralvinkel som spenner over samme bue er 360 grader minus x. Fra setningen over får man da:
<math>180^{\circ} - \beta = \frac 12 (360^{\circ} - x)</math>
c)
<math> 180^{\circ} - \beta = \frac 12(360^{\circ} - x) \\ 360^{\circ} - 2 \beta = 360^{\circ} - x \\ x= 2 \beta </math>
Fra a har man at x er lik to alfa, hvilket betyr at alfa er lik beta.
<math>x = 2 \beta \quad \wedge \quad \alpha = \frac x2 \\ 2 \alpha = 2 \beta \\ \alpha = \beta</math>
Oppgave 9:
a)
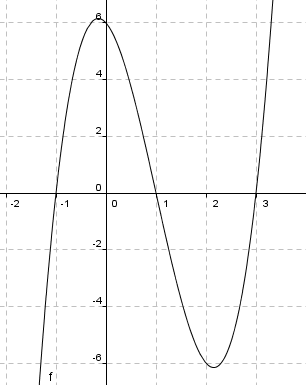
b)
g(x)= 2(x + 2)(x - 1)(x-3)
c)
<math>h(x)= 0,5(x+2)(x-2)(x-2)= 0,5(x+2)(x-2)^2</math>
Oppgave 10:
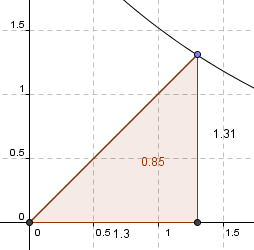
a)
AC = OB = 3
b)
Skravert areale:
<math>\frac 14 \pi r^2 - \frac{3sqrt2}{2} = \frac 94 \pi - \frac{18}{4} = \frac 94(\pi-2)</math>
Oppgave 11:
a)
A = det regner
B = det er meldt regn
<math>P(A)= 0,08 \\ P( \overline{A}) = 1-P(A)= 0,92 </math>
b)
<math>P(B|A)=0,90 \\ P(B| \overline{A}) = 0,10 \\P(B) = P(A) \cdot P(B|A) + P( \overline{A}) \cdot P(B| \overline{A}) = 0,08 \cdot 0,90 + 0,92 \cdot 0,10 = 0,164</math>
c)
<math>P( \overline{A}|B) = \frac{P( \overline{A}) \cdot P(B| \overline{A})}{P(B)} = \frac{0,92 \cdot 0,10}{0,164} = 0,56</math>