1T 2018 høst LØSNING

Diskusjon av denne oppgaven på matteprat

Løsningsforslag laget av Marius Nilsen ved Bergen Private Gymnas

Oppgave 1)

Definisjonen til sinus krever at vi kjenner hypotenusen:

$x^2= 36+ 64 \\ x= \sqrt{100} = 10$

$sin(v)= \frac{8}{10} = 0,8$

Oppgave 2)

$\frac{4x^2-4}{x^2-2x+1} = \frac{4(x-1)(x+1)}{(x-1)(x-1)} = \frac{4(x+1)}{x-1}$

Oppgave 3)

$x^2-4x-12< 0 $

Faktoriserer ved hjelp av ABC formelen:

$x^2-4x-12 =0 \\ x= \frac{-(-4) \pm \sqrt{16-4 \cdot 1 \cdot (-12)} }{2 \cdot 1} \\ x= \frac{4 \pm 8}{2} \\ x= -2 \vee x= 6$

Får da:

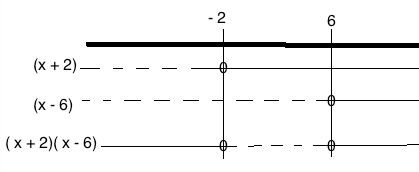
$(x+2)(x-6) < 0$

$x \in < -2, 6 >$

Oppgave 4)

<math> \left[ \begin{align*} y=-x²+4 \\ y=x+2 \end{align*}\right] </math>

Løst ved regning:

$-x²+4=x+2 \\ -x²-x+4-2=0 \\ -x²-x+2=0$

Bruker abc-formelen $x = \frac{-b \pm \sqrt{b^2- 4ac}}{2a}$, a=-1, b=-1, c=2.

$x = \frac{-(-1) \pm \sqrt{(-1)^2- 4\cdot(-1)\cdot 2}}{2\cdot(-1)}$

$x = \frac{1 \pm \sqrt{1+8}}{-2}$

$x_1 = \frac{1+3}{-2} \vee x_2=\frac{1-3}{-2} $

$x_1=-2 \vee x_2=1$

Setter inn x-verdiene i likningen y=x+2.

$y_1=x_1+2=-2+2=0 \\ y_2 =x_2+2=1+2=3$

Løsning: $x_1=-2 \wedge y_1=0 \quad \vee \quad x_2=1 \wedge y_2=3$

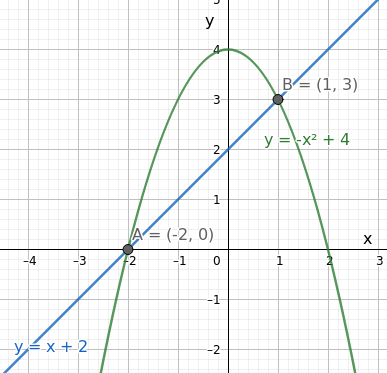
Løst grafisk (du må tegne for hånd):

Den rette linja $y=x+2$ har stigningstall 1 og skjærer y-aksen i y=2.

Andregradsfunksjonen $y=-x²+4$ skjærer y-aksen i y=4. Nullpunktene er x=-2 og x=2. Du kan lage en skisse ut fra disse opplysningene, eventuelt lage en verditabell.

Leser av løsningen i skjæringspunktene mellom de to funksjonene, punkt A og B.

$L=\{(-2,0),(1,3)\}$

Oppgave 5)

$\sqrt{12} - \sqrt[6]{3^3}-\sqrt[4]{9}= \\ \sqrt{4 \cdot 3} - 3^{\frac{3}{6}} - 9^{\frac{1}{4}} =\\ 2\sqrt 3 - 3^{\frac 12} - (3^2)^{\frac 14} =\\ 2 \cdot 3^{\frac 12} - 3^{\frac 12} - 3^{\frac 12} =0 $

Oppgave 6)

$2^x \cdot 2^{\frac x2}= \frac 18 \\ 2^{x+ \frac x2} = 2^{-3} \\ 2^{\frac32x} =2^{-3} \\ \frac 32x = -3\\ 3x=-6 \\ x= -2$

Oppgave 7)

Det er mange måter å løse dette på.

Vi finner radien til $S_1$: $O_1= 2\pi r_1 \\ 5 \pi = 2 \pi r_1 \\ r_1 = \frac{5 \pi}{2 \pi} \\ r_1 = 2,5 $

Vi vet at $ \frac{A_2}{A_1} = 4$

Det betyr at: $ \frac{A_2}{A_1} = \frac{\pi r_2^2}{\pi r_1^2} = 4 \\ \frac{r_2^2}{r_1^2}= 2^2 \\ r_2^2 = 2^2 \cdot r_1^2\\ r_2 = 2r_1 \\r_2= 5 $

Oppgave 8)

a)

$f ´ (0) = (0-1)(0-1)(0+2)= -1 \cdot (-1) \cdot 2 = 2$

Den momentane vekten i null er to.

b)

Fra punkt a vet vi at stigningstallet er to.

Vi har at y= ax + b, altså y = 2x+b.

Siden man spør om stigningen i origo er b lik null; y =2x

c)

$f ´(x)=0 \Rightarrow x= -2 \vee x = 1$

Sjekker så fortegnet til den deriverte på begge sider av punktene:

$f ´(-3) = (-4)(-4)(-1) = - 16 \\ f ´(-1) = (-2)(-2)(1)= 4$

(-2, -6) er et bunnpunkt.

Sjekker mulig terassepunkt ved å sjekke en verdi større enn x=1:

$f ´ (2) = (1)(1)(4) = 4$

Den deriverte skifter ikke fortegn (den deriverte for x=0 er positiv, fra opg. a) og vi kan konkludere at $(1, \frac 34)$ er et terassepunkt.

Oppgave 9

a)

Følgende ti kombinasjoner gir nøyaktig én toer:

$U= \{ (2,1), (2,3), (2,4), (2,5), (2,6), (1,2), (3,2), (4,2), (5,2), (6,2) \} $

Totalt er det $6 \cdot 6=36$ mulige kombinasjoner for ett terningkast med to terninger.

$ P(nøyaktig \, én \, toer)=\frac{10}{36}= \frac{5}{18} $

Sannsynligheten for å få nøyaktig én toer er $\frac{5}{18}$.

b)

Følgende fem kombinasjoner gir summen åtte:

$ U= \{ (2,6), (6,2), (3,5), (5,3), (4,4) \} $

I tre av tilfellene viser ingen av terningene en toer.

$P(ingen \, toer)= \frac{3}{5}$

Sannsynligheten for at ingen av terningene viser en toer er $ \frac{3}{5}$.

Oppgave 10

a)

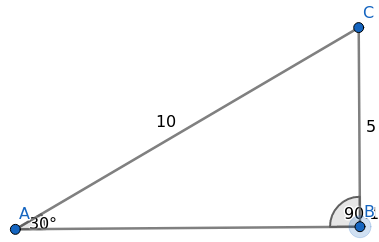
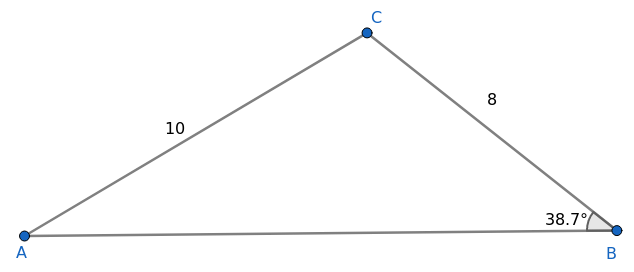
Den korteste lengden av BC får vi dersom $\angle B$ er $90^\circ$. Vi vil da ha en 30-60-90 trekant, hvor den korteste kateten (BC) er halvparten så lang som hypotenusen (AC). Den minste lengden BC kan ha er altså 5 cm.

b)

$\frac{sin\,B}{AC}=\frac{sin\,A}{BC} \\ \frac{sin\,B}{10}=\frac{0,5}{8} \\ sin\,B=\frac{0,5}{8} \cdot 10 \\ sin\,B=\frac{5}{8} $

c)

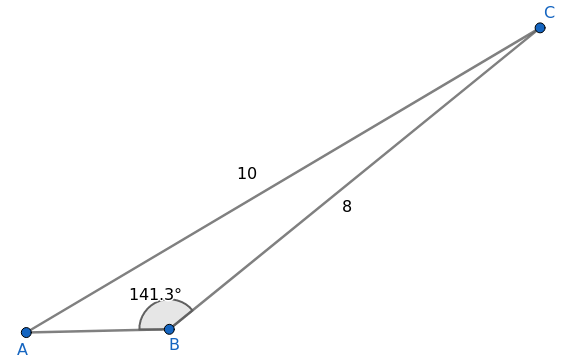
Den andre løsningen blir $\angle B = 180^\circ -38,7^\circ =141,3^\circ $

Skisser av de to mulige trekantene:

Oppgave 11

a)

$ \angle F = \angle D$

Linje gjennom BC er felles i begge trekantene

$AC \parallel DE \Rightarrow \angle C = \angle E$

Trekantene er formlike.

b)

Bruker fomlikheten fra a:

$\frac{8-h}{h} = \frac{x}{x-6} \\ hx = 48-8x-6h+hx \\ 6h=-8x+48 \\ h= - \frac43x+8$

c)

Lengden av AB er 6. x må ligge i intervallet null til seks.

Areal av rektangel:

$A =g(x) = xh = x (- \frac 43x +8) = - \frac 43x^2+8x$

d)

Størst mulig areal:

$g´(x) = - \frac 83 x +8 \\ g ´(x) =0 \\ -\frac 83x +8=0 \\ x=3$

Oppgave 1

a)

b)

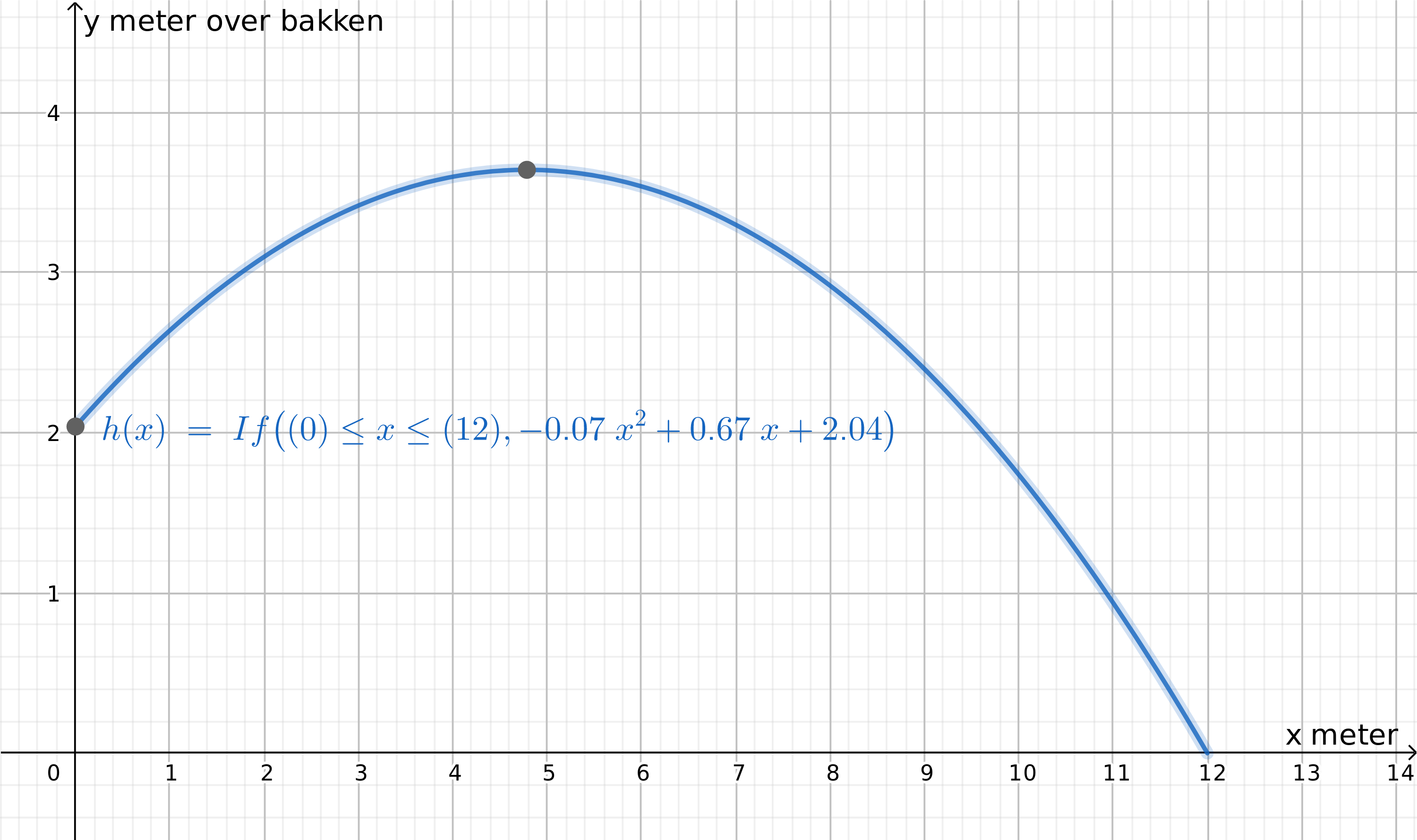
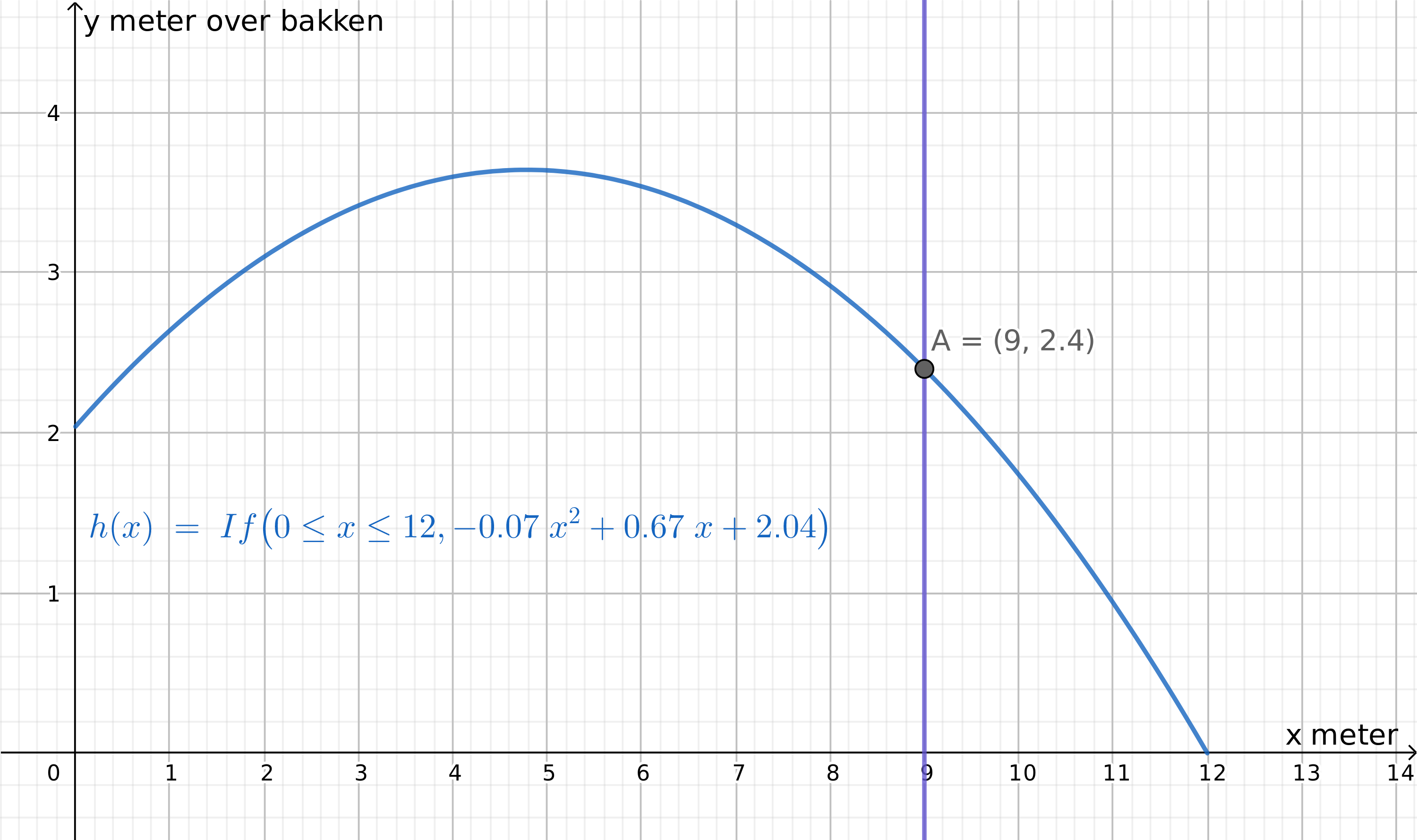
Nettet står midt på banen, 9 meter fra enden av banen på hver side. Lager linjen x=9, som representerer der hvor nettet står, og finner skjæringspunktet mellom linja og grafen til h. Vi ser av punkt A at etter 9 meter, er ballen 2,4 meter over bakken.

For en kvinne som slår ballen fra banens ende, vil ballen gå over nettet (som er 2,24 meter høyt).

For en mann som slår ballen fra banens ende, vil ballen akkurat ikke gå over nettet (som er 2,43 meter høyt). Hvis mannen går litt frem, vil ballen kunne gå over nettet.

Oppgave 2

a)

$f(x)=-x³+k\cdot x² \quad , \quad k \geq 1$

Bestemmer nullpunktene:

$-x³+k\cdot x²=0 \\ x²(-x+k) = 0 \\ x= 0 \vee x=k$