1T 2018 høst LØSNING

Diskusjon av denne oppgaven på matteprat

Løsningsforslag laget av Marius Nilsen ved Bergen Private Gymnas

Oppgave 1)

Definisjonen til sinus krever at vi kjenner hypotenusen:

$x^2= 36+ 64 \\ x= \sqrt{100} = 10$

$sin(v)= \frac{8}{10} = 0,8$

Oppgave 2)

$\frac{4x^2-4}{x^2-2x+1} = \frac{4(x-1)(x+1)}{(x-1)(x-1)} = \frac{4(x+1)}{x-1}$

Oppgave 4)

<math> \left[ \begin{align*} y=-x²+4 \\ y=x+2 \end{align*}\right] </math>

Løst ved regning:

$-x²+4=x+2 \\ -x²-x+4-2=0 \\ -x²-x+2=0$

Bruker abc-formelen $x = \frac{-b \pm \sqrt{b^2- 4ac}}{2a}$, a=-1, b=-1, c=2.

$x = \frac{-(-1) \pm \sqrt{(-1)^2- 4\cdot(-1)\cdot 2}}{2\cdot(-1)}$

$x = \frac{1 \pm \sqrt{1+8}}{-2}$

$x_1 = \frac{1+3}{-2} \vee x_2=\frac{1-3}{-2} $

$x_1=-2 \vee x_2=1$

Setter inn x-verdiene i likningen y=x+2.

$y_1=x_1+2=-2+2=0 \\ y_2 =x_2+2=1+2=3$

Løsning: $x_1=-2 og y_1=0 eller x_2=1 og y_2=3$

Løst grafisk:

Oppgave 5)

$\sqrt{12} - \sqrt[6]{3^3}-\sqrt[4]{9}= \\ \sqrt{4 \cdot 3} - 3^{\frac{3}{6}} - 9^{\frac{1}{4}} =\\ 2\sqrt 3 - 3^{\frac 12} - (3^2)^{\frac 14} =\\ 2 \cdot 3^{\frac 12} - 3^{\frac 12} - 3^{\frac 12} =0 $

Oppgave 6)

$2^x \cdot 2^{\frac x2}= \frac 18 \\ 2^{x+ \frac x2} = 2^{-3} \\ 2^{\frac32x} =2^{-3} \\ \frac 32x = -3\\ 3x=-6 \\ x= -2$

Oppgave 7)

Det er mange måter å løse dette på.

Vi finner radien til $S_1$: $O_1= 2\pi r_1 \\ 5 \pi = 2 \pi r_1 \\ r_1 = \frac{5 \pi}{2 \pi} \\ r_1 = 2,5 $

Vi vet at $ \frac{A_2}{A_1} = 4$

Det betyr at: $ \frac{A_2}{A_1} = \frac{\pi r_2^2}{\pi r_1^2} = 4 \\ \frac{r_2^2}{r_1^2}= 2^2 \\ r_2^2 = 2^2 \cdot r_1^2\\ r_2 = 2r_1 \\r_2= 5 $

Oppgave 8)

a)

$f ´ (0) = (0-1)(0-1)(0+2)= -1 \cdot (-1) \cdot 2 = 2$

Den momentane vekten i null er to.

b)

Fra punkt a vet vi at stigningstallet er to.

Vi har at y= ax + b, altså y = 2x+b.

Siden man spør om stigningen i origo er b lik null; y =2x

c)

$f ´(x)=0 \Rightarrow x= -2 \vee x = 1$

Sjekker så fortegnet til den deriverte på begge sider av punktene:

$f ´(-3) = (-4)(-4)(-1) = - 16 \\ f ´(-1) = (-2)(-2)(1)= 4$

(-2, -6) er et bunnpunkt.

Sjekker mulig terassepunkt ved å sjekke en verdi større enn x=1:

$f ´ (2) = (1)(1)(4) = 4$

Den deriverte skifter ikke fortegn (den deriverte for x=0 er positiv, fra opg. a) og vi kan konkludere at $(1, \frac 34)$ er et terassepunkt.

Oppgave 9

a)

Følgende ti kombinasjoner gir nøyaktig én toer:

$U= \{ (2,1), (2,3), (2,4), (2,5), (2,6), (1,2), (3,2), (4,2), (5,2), (6,2) \} $

Totalt er det $6 \cdot 6=36$ mulige kombinasjoner for ett terningkast med to terninger.

$ P(nøyaktig \, én \, toer)=\frac{10}{36}= \frac{5}{18} $

Sannsynligheten for å få nøyaktig én toer er $\frac{5}{18}$.

b)

Følgende fem kombinasjoner gir summen åtte:

$ U= \{ (2,6), (6,2), (3,5), (5,3), (4,4) \} $

I tre av tilfellene viser ingen av terningene en toer.

$P(ingen \, toer)= \frac{3}{5}$

Sannsynligheten for at ingen av terningene viser en toer er $ \frac{3}{5}$.

Oppgave 10

a)

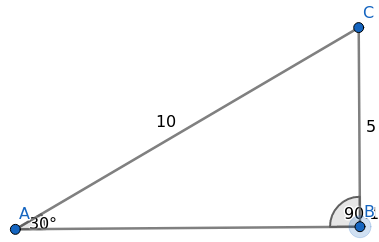
Den korteste lengden av BC får vi dersom $\angle B$ er $90^\circ$. Vi vil da ha en 30-60-90 trekant, hvor den korteste kateten (BC) er halvparten så lang som hypotenusen (AC). Den minste lengden BC kan ha er altså 5 cm.

b)

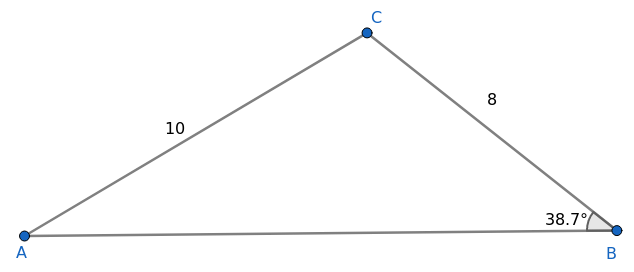
$\frac{sin\,B}{AC}=\frac{sin\,A}{BC} \\ \frac{sin\,B}{10}=\frac{0,5}{8} \\ sin\,B=\frac{0,5}{8} \cdot 10 \\ sin\,B=\frac{5}{8} $

c)

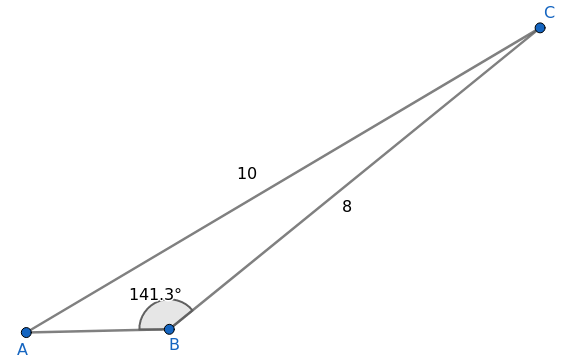
Den andre løsningen blir $\angle B = 180^\circ -38,7^\circ =141,3^\circ $

Skisser av de to mulige trekantene:

Oppgave 11

a)

$ \angle F = \angle D$

Linje gjennom BC er felles i begge trekantene

$AC \parallel DE \Rightarrow \angle C = \angle E$

Trekantene er formlike.

b)

Bruker fomlikheten fra a:

$\frac{8-h}{h} = \frac{x}{x-6} \\ hx = 48-8x-6h+hx \\ 6h=-8x+48 \\ h= - \frac43x+8$

c)

Lengden av AB er 6. x må ligge i intervallet null til seks.

Areal av rektangel:

$A =g(x) = xh = x (- \frac 43x +8) = - \frac 43x^2+8x$

d)

Størst mulig areal:

$g´(x) = - \frac 83 x +8 \\ g ´(x) =0 \\ -\frac 83x +8=0 \\ x=3$