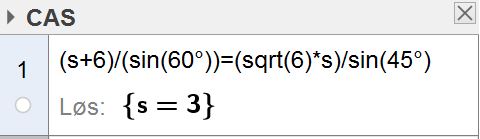1T 2018 vår LØSNING

Oppgaven som pdf

Diskusjon av oppgaven på matteprat

Løsning laget av LektorNilsen

DEL EN

Oppgave 1

<math> \left[ \begin{align*}5x +2y =4 \\ 3x + 4y = -6 \end{align*}\right] </math>

Ganger første likning med -2 for å bruke addisjon, slik at y forsvinner.

<math> \left[ \begin{align*}- 10x - 4y = -8\\ 3x + 4y = -6 \end{align*}\right] </math>

Legger likningen sammen og får

$-7x = -14 \\ x=2$

Setter x = 2 inn i første likning og får at y er:

$5x+2y =4 \\ 10 + 2y = 4 \\ 2y = -6 \\ y = -3$

Løsning: $x= 2 \wedge y= -3$

Oppgave 2

$3 \cdot 10^x = 3000 \\ 10^x = 1000 \\ x lg 10 = lg 1000 \\ x \cdot 1 = lg 1000 \\ x = 3$

Oppgave 3

$ \frac{(0,5 \cdot 10^6)^2}{0,2 \cdot 10^{-4} + 3 \cdot 10^{-5}} = \frac{0,25 \cdot 10^{12}}{2 \cdot 10^{-5} + 3 \cdot 10^{-5}} = \frac{25 \cdot 10^{10}}{5 \cdot 10^{-5}} = 5 \cdot 10^{15} $

Oppgave 4

$\sqrt{15 }\cdot \sqrt5 - \sqrt{48} = \sqrt {3 \cdot 5 \cdot 5} -\sqrt{4 \cdot 4 \cdot 3 } = 5 \sqrt3 - 4 \sqrt 3 =\sqrt 3$

Oppgave 5

$lg1000 \cdot lg \sqrt[3]{10} \cdot lg \sqrt[5]{10^2} \cdot lg 0,00001 \\= lg10^3 \cdot lg10^{\frac{1}{3}} \cdot lg10^{\frac{2}{5}} \cdot lg10^{-5} \\ = 3 \cdot \frac{1}{3} \cdot \frac{2}{5} \cdot (-5) = -2$

a)

$x (x+2) (x-4) = x (x^2-4x+2x-8) = x ( x^2 - 2x - 8) = x^3 -2x^2-8x$

b)

$x^3 -2x^2-8x = 0 \\ x (x+2) (x-4) = 0 \\ x=-2 \wedge x=0 \wedge x=4$

Oppgave 7

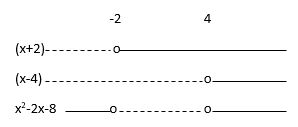
$ x^2-2x-8=0 \\ (x+2)(x-4)=0 \\ x=-2 \wedge x=4 $

$ x^2-2x-8 \geq 0 $ for $x<-2$ og $x>4$

Oppgave 8

Bruker abc-formelen $x = \frac{-b \sqrt{b^2- 4ac}}{2a}$ for å finne funksjonens nullpunkter, a=1, b=k, c=4.

$ x^2 +kx + 4 = 0 \\ x = \frac{-k \sqrt{k^2- 4 \cdot 1 \cdot 4}}{2 \cdot 1} \\ x = \frac{-k \sqrt{k^2- 16}}{2} $

Dersom likningen er uløselig, har grafen til f ingen skjæringspunkter med x-aksen (dvs. ingen nullpunkter). Dette skjer dersom verdien under kvadratroten er negativ, siden kvadratroten av et negativt tall ikke gir noen reelle løsninger.

Dersom verdien under kvadratroten er 0, får likningen bare én løsning, og grafen til f bare ett skjæringspunkt med x-aksen (dvs. ett nullpunkt).

Dersom verdien under kvadratroten er positiv, får likningen to løsninger, og grafen til f to skjæringspunkter med x-aksen (dvs. to nullpunkt).

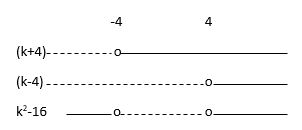
Vi løser likningen $k^2-16 = 0$ for å finne hvilke verdier av k oppfyller de ulike mulighetene.

$k^2=16 \\ k= \pm \sqrt{16} \\ k=-4 \wedge k=4$

Vi ser at grafen til f har

$\bullet$ ingen skjæringspunkter med x-aksen for $-4<k<4$

$\bullet$ ett skjæringspunkt med x-aksen for $k=-4$ og $k=4$

$\bullet$ to skjæringspunkter med x-aksen for $k<-4$ og $k>4$

a)

$ \frac{x+2+\frac{1}{x}}{\frac{x}{3}-\frac{1}{3x}} = \frac{3x(x+2+\frac{1}{x})}{3x(\frac{x}{3}-\frac{1}{3x})} = \frac{3x^2+6x+3}{x^2-1} $

b)

$ \frac{x+2+\frac{1}{x}}{\frac{x}{3}-\frac{1}{3x}} = \frac{3x^2+6x+3}{x^2-1} = \frac{3(x^2+2x+1)}{(x+1)(x-1)} = \frac{3(x+1)(x+1)}{(x+1)(x-1)} = \frac{3x+3}{x-1}$

a)

$f(x)=x^3+2x^2+1$

Gjennomsnittlig vekstfart $a=\frac{y_2-y_1}{x_2-x_1}$

$x_1=-2$

$x_2=2$

$y_1=f(-2)=(-2)^3+2\cdot(-2)^2+1=-8+8+1=1$

$y_2=f(2)=2^3+2\cdot2^2+1=8+8+1=17$

$a=\frac{17-1}{2-(-2)}=\frac{16}{4}=4$

Den gjennomsnittlige vekstfarten til f i intervallet [-2,2] er 4.

b)

$f(x)=x^3+2x^2+1$

$f'(x)=3x^2+4x$

Likning for tangenten i et punkt $(x_1,y_1): (y-y_1)=a(x-x_1)$

$x_1=1$

$y_1=f(1)=1^3+2\cdot1^2+1=1+2+1=4$

$a=f'(1)=3\cdot 1^2 +4 \cdot 1 = 3+4=7$

Likning for tangenten til grafen til f i punktet $(1,f(1))$:

$(y-4)=7(x-1) \\ y=7x-7+4 \\ y=7x-3$

Oppgave 11

Når man kaster to terninger er det $6\cdot 6 = 36$ mulige utfall totalt.

Utfallsrom for at terningene viser samme antall øyne:

$U_1=\{(1,1),(2,2),(3,3),(4,4),(5,5),(6,6)\}$. Det gir oss 6 gunstige utfall.

Sannsyngliheten for at terningne viser samme antall øyne er $\frac{6}{36}$

Utfallsrom for at summen av antall øyne er 5 eller mindre:

$U_2=\{(1,1),(1,2),(2,1),(2,2),(1,3),(3,1),(2,3),(3,2),(1,4),(4,1)\}$. Det gir oss 10 gunstige utfall.

Sannsyngliheten for at summen av antall øyne er 5 eller mindre er $\frac{10}{36}$.

Det er altså alternativ 2, "summen av antall øyne er 5 eller mindre", som er mest sannsynlig.

a)

Bruker Pytagorassetningen til å finne lengden av DC.

$(DC)^2 = (AC)^2 - (AD)^2 \\ (DC)^2 = s^2 - (\frac{s}{2})^2 \\ (DC)^2 = \frac{4s^2}{4} - \frac{s^2}{4} \\ DC=\sqrt{\frac{3s^2}{4}} \\ DC = \frac{s \sqrt{3}}{2}$

b)

I en rettvinklet trekant er $sin v = \frac{motstående katet}{hypotenus}$

$sin 60° = \frac{DC}{AC} \\ sin 60° = \frac{\frac{s \sqrt{3}}{2}}{s} \\ sin 60° = \frac{\sqrt{3}}{2}$

c)

Vi finner høyden SR til $\Delta PQR$. Vi vet fra forrige deloppgave at $sin 60° = \frac{\sqrt{3}}{2}$ og vi vet fra oppgaveteksten at $PR=2\sqrt{3}$

$sin(v) = \frac{motstående katet}{hypotenus} \\ sin 60° = \frac{SR}{PR} \\ \frac{\sqrt{3}}{2} = \frac{SR}{2\sqrt{3}} \\ SR = \frac{\sqrt{3}\sqrt{3}\cdot2}{2} \\ SR = 3$

Vi kan nå bestemme arealet til $\Delta PQR$.

$A=\frac{grunnlinje \cdot høyde}{2} \\ A=\frac{PQ \cdot SR}{2} \\ A=\frac{8 \cdot 3}{2} \\ A=12$

Du kan også bestemme arealet til $\Delta PQR$ ved å bruke arealsetningen.

d)

Vi begynner med å finne lengden av PS. Siden $\Delta{PSR}$ er en 30°-60°-90° trekant, er den korteste kateten halvparten så lang som hypotenusen. Det vil si at $PS=\frac{PR}{2}=\frac{2\sqrt{3}}{2}=\sqrt{3}$. Du kan også finne lengen av PS ved hjelp av Pytagorassetningen.

Vi kan nå finne $tanQ$. Vi vet at i en rettvinklet trekant er $tan(v) = \frac{motstående katet}{hosliggende katet}$. Fra oppgave c) vet vi at SR = 3, og fra oppgaveteksten vet vi at PQ=8.

$tanQ = \frac{SR}{SQ} \\ tanQ = \frac{3}{PQ-PS} \\ tanQ = \frac{3}{8-\sqrt{3}}$

Oppgave 13

Graf E er grafen til funksjonen p, fordi p er den eneste funksjonen hvor konstantleddet er 0. Dersom konstantleddet til en funksjon er null, vil grafen skjære y-aksen i origo, og graf E er derfor den eneste som passer.

Graf F er grafen til funksjonen r, fordi r er den eneste funksjonen med negativ koeffisient i andregradsleddet. Grafen til en andregradsfunksjon med negativt andregradsledd vil alltid bue nedover ("surt fjes"), og graf F er derfor den eneste som passer.

Funksjonene q og s har begge konstantleddet -2, dvs. at skjæringspunktet med y-aksen er i y=-2. Graf A og B passer ikke til det, og vi sitter igjen med graf C og D. Disse er ganske like, men har bunnpunktet på forskjellig sted. Vi kan finne x-verdien til bunnpunktet for begge funksjonene.

$q'(x)=2x+2$

Setter $q'(x)=0 \\ 2x+2=0 \\ 2x=-2 \\ x= -1$

$s'(x)=2x-2$

Setter $s'(x)=0 \\ 2x-2=0 \\ 2x=2 \\ x=1$

Vi ser at graf D er grafen til funksjonen s, fordi den har bunnpunktet i x=1.

Graf C er grafen til funksjonen q, fordi den har bunnpunktet i x=-1.

Du kan også finne de riktige grafene til funksjonene q og s ved å finne symmetrilinja x til funksjonene, ved hjelp av formelen $x=\frac{-b}{2a}$.

DEL 2

a)

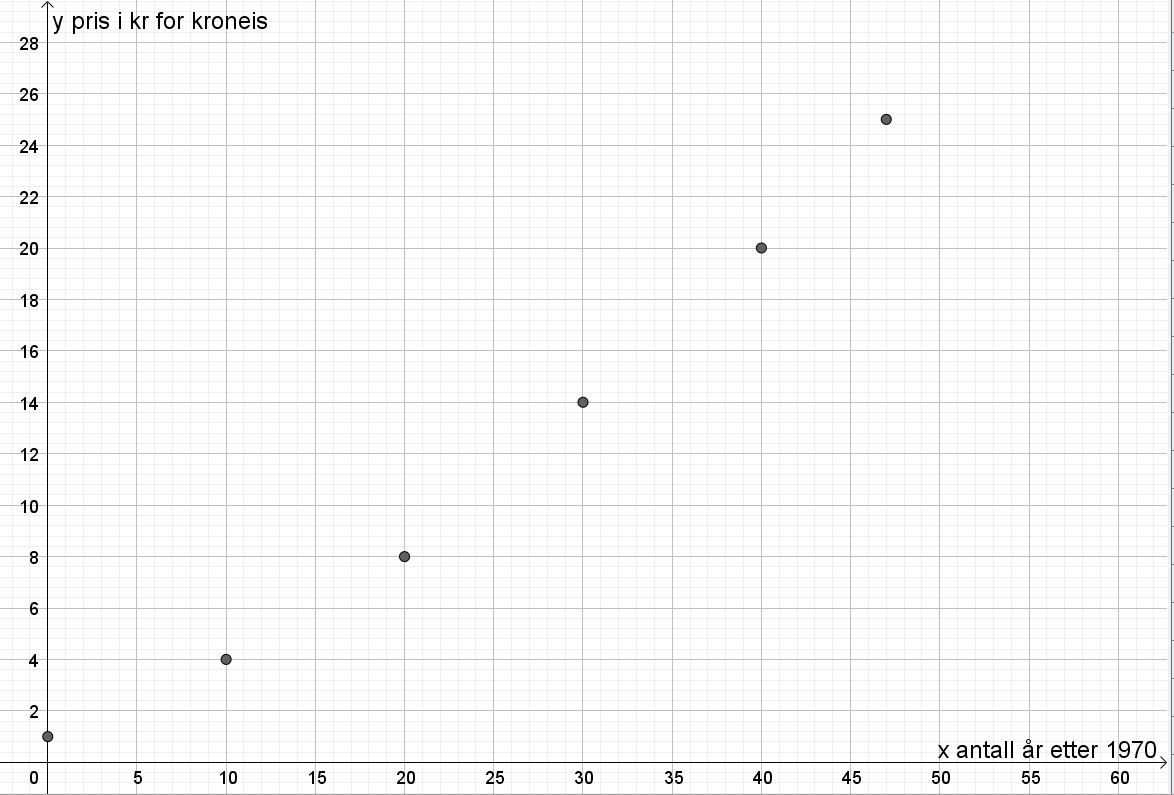
Bruker Geogebra.

b)

c)

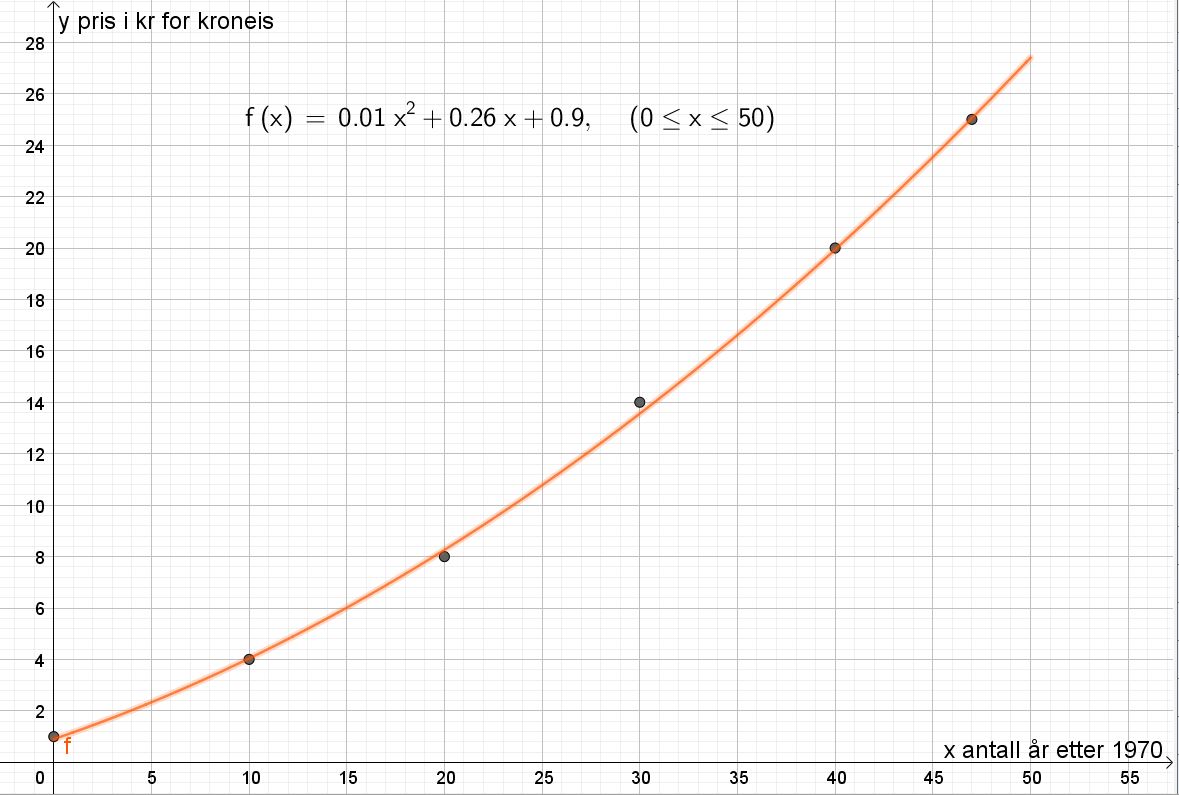
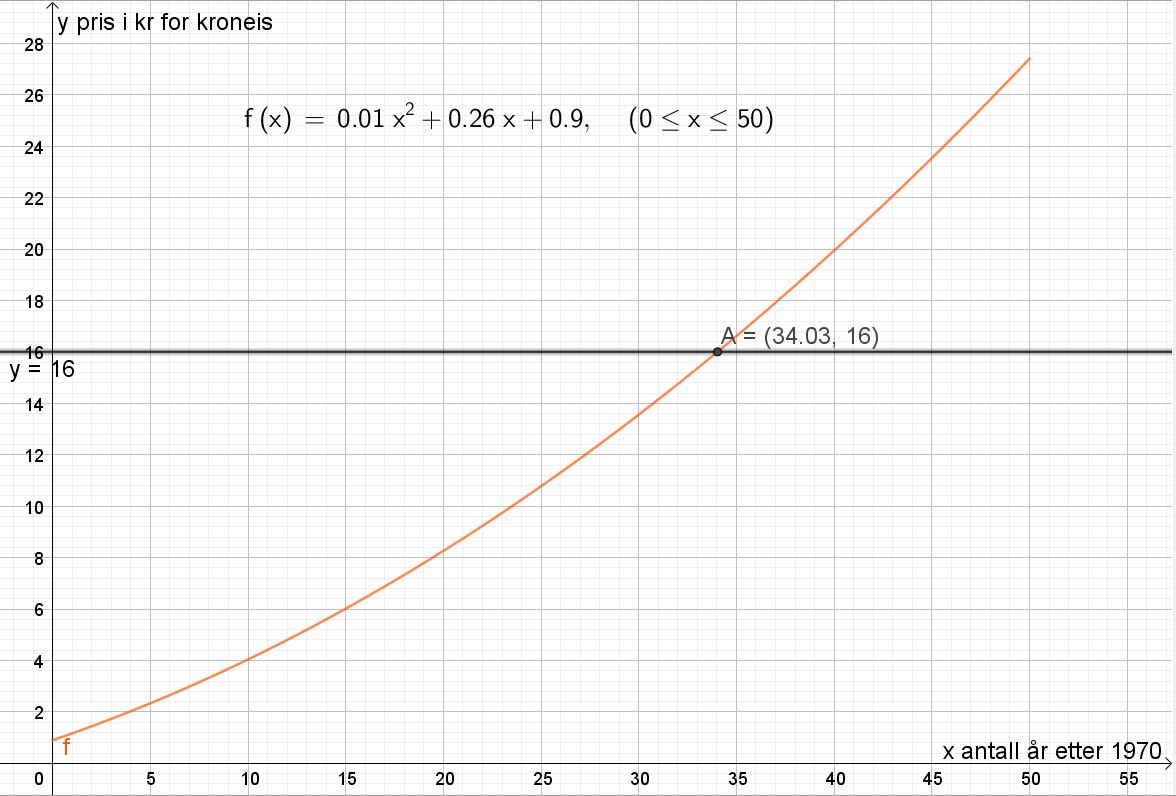
Lager linja y=16. Bruker skjæring mellom to objekter for å finne skjæringspunktet med grafen til funksjonen $f$.

Isen kostet 16 kr 34 år etter 1970, det vil si i 2004.

d)

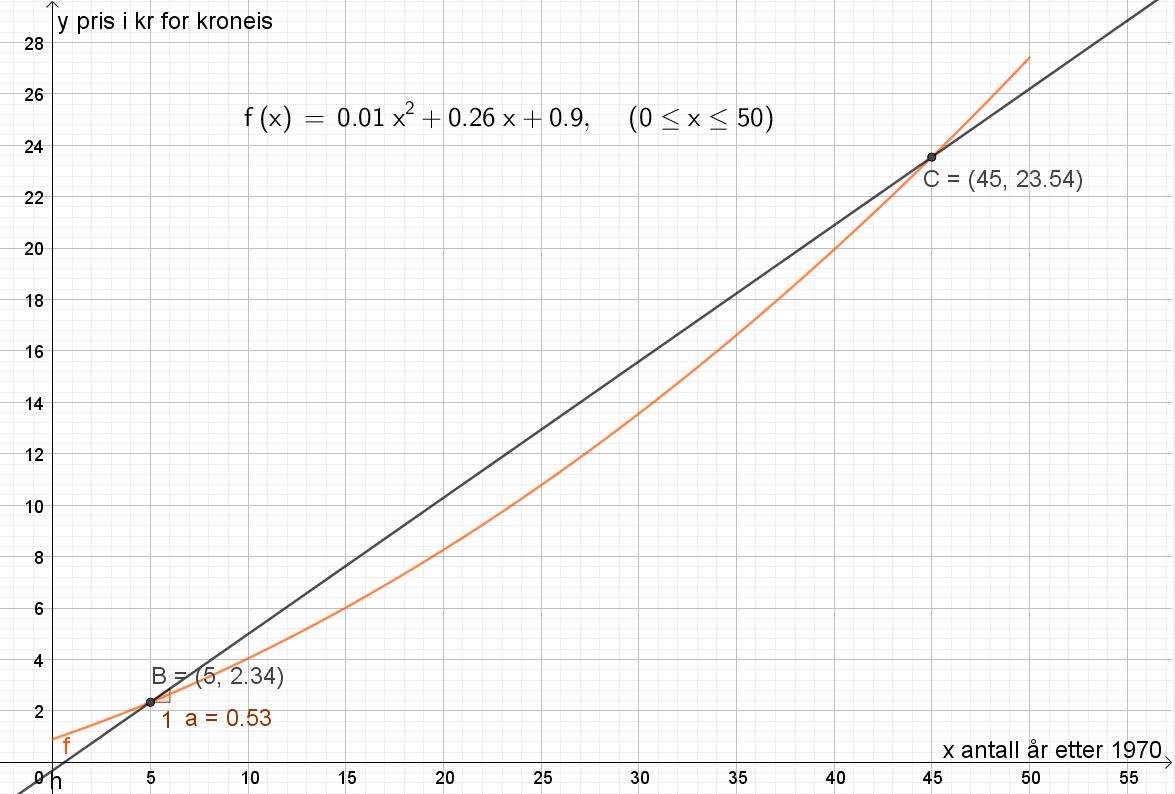
1975 er 5 år etter 1970, og 2015 er 45 år etter 1970. Lager derfor punkt B=(5,f(5)) og C=(45,f(45)). Lager en linje mellom punkt B og C, og finner linjens stigning, $a=0.53$.

Prisen for en kroneis har steget i gjennomsnitt med 0.53 kr per år fra 1975 til 2015.

a)

Oppgave 3

Siden summen av vinklene i en trekant er 180°, er den siste vinkelen i trekanten $180°-45°-75°=60°$.

Bruker videre sinussetningen $\frac{a}{sinA}=\frac{b}{sinB}$ for å bestemme $s$ i CAS i Geogebra. Husk gradertegnet for vinkler i CAS.