Forskjell mellom versjoner av «1T 2021 vår LK20 LØSNING»
| (21 mellomliggende revisjoner av samme bruker vises ikke) | |||
| Linje 191: | Linje 191: | ||
[[File: 1T_V21_del2_14a.png|200px]] | [[File: 1T_V21_del2_14a.png|200px]] | ||
| − | Her ser det ut som nullpunktene til g har inverse verdier av nullpunktene til f. Men det kan også se ut som nullpunktene til f er 6 ganger større enn nullpunktene til g. Jeg tester med flere eksempler. | + | Her ser det ut som nullpunktene til g har inverse verdier av nullpunktene til f. Men det kan også se ut som nullpunktene til f er 6 ganger større enn nullpunktene til g. Jeg tester med flere eksempler, for eksempel dette: |
| + | |||
| + | [[File: 1T_V21_del2_14a2.png|300px]] | ||
I oppgave b skal jeg finne ut om dette gjelder for alle slike polynomer. | I oppgave b skal jeg finne ut om dette gjelder for alle slike polynomer. | ||
| Linje 197: | Linje 199: | ||
===b)=== | ===b)=== | ||
| − | Bruker CAS i Geogebra til å sjekke sammenhengen mellom nullpunkter for alle slike polynomer med "omvendt rekkefølge" på koeffisientene a,b og c. Ser at for | + | Bruker CAS i Geogebra til å sjekke sammenhengen mellom nullpunkter for alle slike polynomer med "omvendt rekkefølge" på koeffisientene a,b og c. Ser at for to slike polynomer h og i, så er forholdet mellom nullpunktene slik at nullpunktene til funksjonen h, er $\frac{c}{a}$ ganger nullpunktene til funksjonen i. |
| + | |||
| + | [[File: 1T_V21_del2_14b.png|400px]] | ||
| + | |||
| + | =Oppgavetype 3= | ||
| + | |||
| + | I disse oppgavene får du presentert en situasjon eller en problemstilling som du selv må undersøke og utforske. | ||
| + | |||
| + | ==Oppgave 15== | ||
| + | |||
| + | Jeg bruker glidere i Geogebra til å utforske hvilke verdier av a og b som gir et skjæringspunkt der begge koordinatene er positive hele tall. Sette gliderne til å være hele tall fra 1 til f.eks. 20. | ||
| + | |||
| + | [[File: 1T-V21-del3-15.png|600px]] | ||
| + | |||
| + | Jeg kan bruke grafene til å begynne å se sammenhenger, men jeg kan også finne skjæringspunktet mellom g og f ved regning, ved å sette f=g. | ||
| + | |||
| + | $ax=\frac{b}{x}$ | ||
| + | |||
| + | $x^2=\frac{b}{a}$ | ||
| + | |||
| + | $x=\sqrt{\frac{b}{a}}$ | ||
| + | |||
| + | For at x skal være et helt positivt tall, må b/a gi et kvadrattall. Alle kombinasjoner av b/a som gir et kvadrattall, gir et skjæringspunkt der x er et positivt helt tall. | ||
| + | |||
| + | F.eks: | ||
| + | |||
| + | a=1, b=1,4,9,16,25... | ||
| + | |||
| + | a=2, b=2,8,18,36,50... | ||
| + | |||
| + | a=3, b=3,12,27,... | ||
| + | |||
| + | a=n, b=k*n, der n er et naturlig tall og k er et kvadrattall. | ||
| + | |||
| + | Både x- og y-koordinatene i skjæringspunktet skulle være positive, hele tall. Jeg må sjekke at alle kombinasjoner av b/a som gir kvadrattall, ikke bare gir en x-koordinat som er et positivt helt tall, men også en y-koordinat som er et positivt helt tall. | ||
| + | |||
| + | Finner y-koordinaten hvis $x=\sqrt{\frac{b}{a}}$ | ||
| + | |||
| + | $f(\sqrt{\frac{b}{a}})=a\cdot \sqrt{\frac{b}{a}} = a\cdot \frac{\sqrt{a}\sqrt{b}}{\sqrt{a}\sqrt{a}} = a\cdot \frac{\sqrt{ab}}{a}=\sqrt{ab}$ | ||
| + | |||
| + | Setter inn a=n, b=k*n, der n er et naturlig tall og k er et kvadrattall. | ||
| + | |||
| + | $y = \sqrt{ab} = \sqrt{n\cdot k\cdot n} = n\sqrt{k}$ | ||
| + | |||
| + | Et naturlig tall ganger roten av et kvadrattall vil alltid gi et positivt, helt tall. | ||
| + | |||
| + | Dermed har vi vist at for alle a=n og b=k*n, der n er et naturlig tall og k er et kvadrattall, så vil skjæringspunktet mellom f og g ha koordinater som er positive, hele tall. | ||
| + | |||
| + | ==Oppgave 16== | ||
| + | |||
| + | Cosinussetningen: | ||
| + | |||
| + | $a^2=b^2+c^2-2bc\cdot cos A$ | ||
| + | |||
| + | Siri har likningen: | ||
| + | |||
| + | $a^2=8^2+x^2-8x$ | ||
| + | |||
| + | hvilket må bety at | ||
| + | |||
| + | $2 cos A = 1$ | ||
| + | |||
| + | $cos A = \frac{1}{2}$ | ||
| + | |||
| + | $A=60^o$ | ||
| + | |||
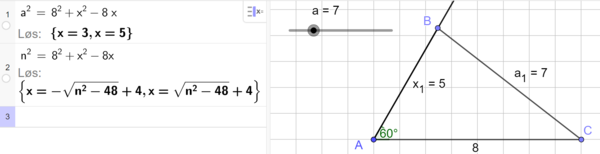
| + | Bruker en glider for a i Geogebra, og bruker CAS til å regne ut mulige verdier av x (linje 1 i CAS). Bruker grafikkfeltet til å tegne de ulike trekantene. Ser av linje 2 i CAS at a (n i linje 2) må være minst 7 for at vi skal få en trekant som tilfredsstiller likningen. For eksempel: | ||
| + | |||
| + | [[File: 1T_V21_del3_16.png|600px]] | ||
| + | |||
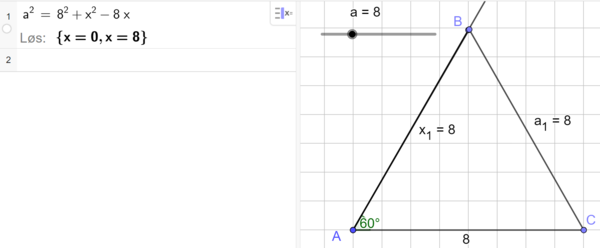
| + | Er a = 8, får vi en likesidet trekant. | ||
| + | |||
| + | [[File: 1T_V21_del3_16b.png|600px]] | ||
| + | |||
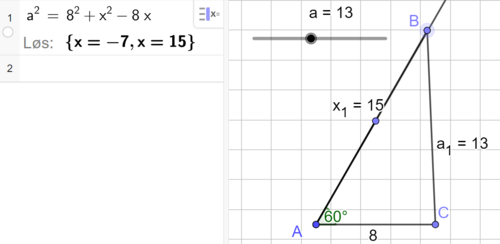
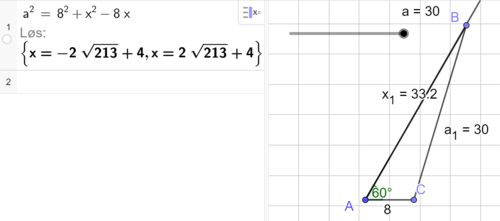
| + | Vi har mange mulige trekanter, videre, f.eks: | ||
| + | |||
| + | [[File: 1T_V21_del3_16c.png|500px]] | ||
| − | [[File: | + | [[File: 1T_V21_del3_16d.png|500px]] |
Revisjonen fra 17. apr. 2022 kl. 10:37
Eksamen 1T vår 2021 LK20 Fagfornyelsen
Diskusjon av oppgaven på matteprat
Løsning laget av Kristian Saug
Oppgavetype 1
I oppgavetype 1 skal du bare oppgi svaret, uten begrunnelse. Vi gir allikevel en liten begrunnelse her, for å forstå hvordan vi har kommet frem til svaret.
Oppgave 1
Svar: $a=-1$
Begrunnelse: Vi har $f(x) = ax+8$, og punktet $(4,4)$. Løser likningen $f(4)=4$.
$a\cdot 4 + 8 = 4 $
$ 4a = 4-8 $
$ a = \frac{-4}{4}$
$ a = -1 $
Oppgave 2
Svar: $BC = 6$
Begrunnelse: $sin\,A = \frac{\text{motstående katet}}{\text{hypotenus}}=\frac{BC}{AC}=\frac{3}{5}=\frac{6}{10} \quad \Rightarrow \quad BC = 6$
Oppgave 3
Svar: $k=-2$
Begrunnelse:
Ser at $x=2$ er løsningen for $x^3+x^2-2x-8=0$. Da må k være lik -2.
Oppgave 4
Svar: $k=-1$
Begrunnelse: Dersom likningen bare har ett svar, er diskriminanten i andregradsformelen lik 0.
$(2k)^2-4\cdot 1\cdot (-2k-1)=0$
$4k^2+8k+4=0$
$4(k^2+2k+1)=0$
$k=-1$
Oppgave 5
Svar: 280 km
Begrunnelse:
$A(x)=1200$
$B(x)=\frac{10}{4} x+500$
Setter A(x)=B(x):
$\frac{10}{4} x+500 = 1200$
$x=\frac{700\cdot 4}{10}$
$x=280$
Oppgave 6
Svar: Alternativ 2, $\frac{m}{n}<\frac{m+2}{n+2}$, er riktig.
Begrunnelse: Siden $m,n\in \mathbb{N}$, det vil si er naturlige tall, altså positive hele tall som 1,2,3... og $n>m$ har vi $0<\frac{m}{n}<1$ for alle verdier av $m$ og $n$. Dersom både $m$ og $n$ øker med 2, vil forholdet mellom disse tallene bli større (telleren vil utgjøre en større andel av nevneren). Du kan selv teste det med noen enkle tall.
Oppgave 7
Svar: $a=20$
Begrunnelse:
$f(x)=-5x^2+ax+1$
$f'(x)=-10x+a$
Toppunktet er i $x=2$, setter $f'(2)=0$
$-10\cdot 2+a=0$
$a=20$
Oppgave 8
Svar: $r=16, s=2, t=4$
Begrunnelse:
Dette følger av første kvadratsetning. vi har $4x^2+16x+16=(2x)^2+2\cdot 2x\cdot 4+4^2=(2x+4)^2$
Oppgavetype 2
I oppgavetype 2 skal du vise utregninger, forklare framgangsmåter du har brukt, og begrunne resultater.
Oppgave 9
a)
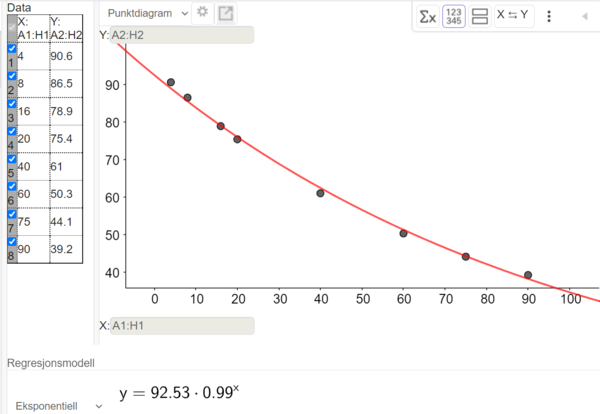
Skriver tabellen i regnearket på Geogebra, og utfører en regresjonsanalyse. Velger eksponentiell modell.
Modellen for temperaturen T i geleen, x minutter etter avkjøling er: $T(x)=92.5\cdot 0.99^x$
b)
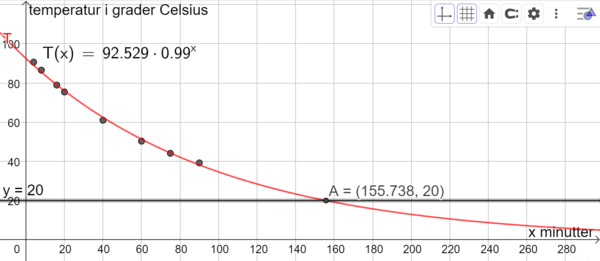
Temperaturen i geleen vil ikke bli lavere enn romtemperaturen, altså 20 grader Celsius. Bruker Geogebra til å finne ut hvor mange minutter det tar før geleen er 20 grader, ved å skrive y=20 og bruke "skjæring mellom to objekt" mellom denne linja og grafen til T. Det tar 155,7 minutter før temperaturen i geleen har nådd 20 grader.
Gyldighetsområdet til modellen er $x\in [0,155.7]$
Oppgave 10
Funksjonen $f(x)=x^2-x-6$ har to nullpunkter, x=-2 og x=3. Skissen viser grafen til denne funksjonen.
Skissen kan brukes til å se at ulikheten $x^2-x-6>0$ har løsningene x<-2 og x>3 (de områdene hvor grafen er over x-aksen).
Dette er samme løsninger som for ulikheten $x^2-x>6$.
Oppgave 11
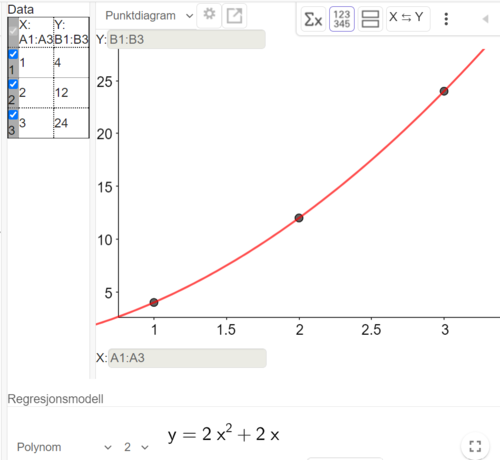
Bruker regresjonsanalyse i Geogebra til å finne et uttrykk for antall fyrstikker f som funksjon av figurnummer x.
$f(x)=2x^2+2x$
a)
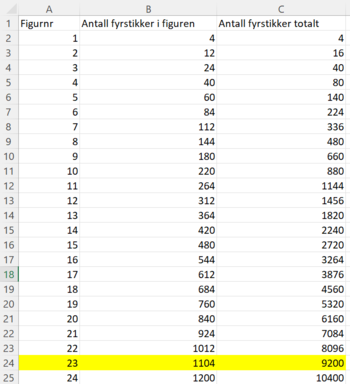
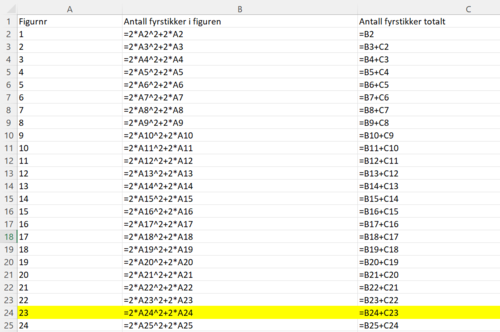
Bruker Excel til å lage en oversikt over antall fyrstikker brukt per figur (bruker da funksjonen jeg fant i Geogebra), og en oversikt over antall fyrstikker brukt totalt. Jeg har bare 10000 fyrstikker totalt, og ser at jeg da kan lage 23 figurer.
b)
Jeg har 10000-9200 = 800 fyrstikker igjen etter å ha laget den siste figuren.
Oppgave 12
Bruker regresjonsanalyse i Geogebra.
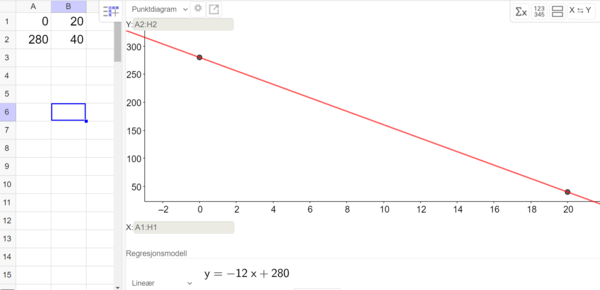
a)
$y=-12x+280$ er en lineær modell som viser hvor mange kaniner det vil være i området om x måneder.
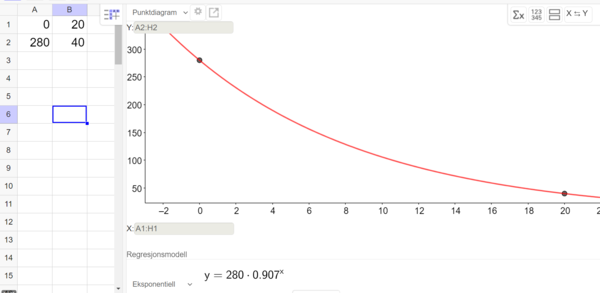
b)
$y = 280\cdot 0.907^x$ er en eksponentiell modell som viser hvor mange kaniner det vil være i området om x måneder.
Oppgave 13
Bruker CAS i Geogebra.
Linje 1: definerer f(x)
Linje 2: Finner x-verdien til punktene hvor den deriverte har verdi 1/2 (stigningstallet til tangenten er 1/2).
Linje 3 og 5: finner uttrykket for tangenten i de to punktene hvor stigningstallet til tangenten er 1/2.
Linje 4 og 6: finner skjæringspunktet til tangentene med x-aksen (y-verdien er lik 0).
Svar: $x=-\sqrt{2}+2$ og $x=\sqrt{2}+2$
Oppgave 14
a)
Bruker CAS i Geogebra til å sjekke sammenhengen mellom nullpunktene til f og g i det gitte eksempelet.
Her ser det ut som nullpunktene til g har inverse verdier av nullpunktene til f. Men det kan også se ut som nullpunktene til f er 6 ganger større enn nullpunktene til g. Jeg tester med flere eksempler, for eksempel dette:
I oppgave b skal jeg finne ut om dette gjelder for alle slike polynomer.
b)
Bruker CAS i Geogebra til å sjekke sammenhengen mellom nullpunkter for alle slike polynomer med "omvendt rekkefølge" på koeffisientene a,b og c. Ser at for to slike polynomer h og i, så er forholdet mellom nullpunktene slik at nullpunktene til funksjonen h, er $\frac{c}{a}$ ganger nullpunktene til funksjonen i.
Oppgavetype 3
I disse oppgavene får du presentert en situasjon eller en problemstilling som du selv må undersøke og utforske.
Oppgave 15
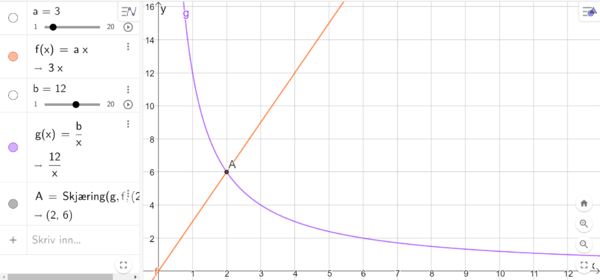
Jeg bruker glidere i Geogebra til å utforske hvilke verdier av a og b som gir et skjæringspunkt der begge koordinatene er positive hele tall. Sette gliderne til å være hele tall fra 1 til f.eks. 20.
Jeg kan bruke grafene til å begynne å se sammenhenger, men jeg kan også finne skjæringspunktet mellom g og f ved regning, ved å sette f=g.
$ax=\frac{b}{x}$
$x^2=\frac{b}{a}$
$x=\sqrt{\frac{b}{a}}$
For at x skal være et helt positivt tall, må b/a gi et kvadrattall. Alle kombinasjoner av b/a som gir et kvadrattall, gir et skjæringspunkt der x er et positivt helt tall.
F.eks:
a=1, b=1,4,9,16,25...
a=2, b=2,8,18,36,50...
a=3, b=3,12,27,...
a=n, b=k*n, der n er et naturlig tall og k er et kvadrattall.
Både x- og y-koordinatene i skjæringspunktet skulle være positive, hele tall. Jeg må sjekke at alle kombinasjoner av b/a som gir kvadrattall, ikke bare gir en x-koordinat som er et positivt helt tall, men også en y-koordinat som er et positivt helt tall.
Finner y-koordinaten hvis $x=\sqrt{\frac{b}{a}}$
$f(\sqrt{\frac{b}{a}})=a\cdot \sqrt{\frac{b}{a}} = a\cdot \frac{\sqrt{a}\sqrt{b}}{\sqrt{a}\sqrt{a}} = a\cdot \frac{\sqrt{ab}}{a}=\sqrt{ab}$
Setter inn a=n, b=k*n, der n er et naturlig tall og k er et kvadrattall.
$y = \sqrt{ab} = \sqrt{n\cdot k\cdot n} = n\sqrt{k}$
Et naturlig tall ganger roten av et kvadrattall vil alltid gi et positivt, helt tall.
Dermed har vi vist at for alle a=n og b=k*n, der n er et naturlig tall og k er et kvadrattall, så vil skjæringspunktet mellom f og g ha koordinater som er positive, hele tall.
Oppgave 16
Cosinussetningen:
$a^2=b^2+c^2-2bc\cdot cos A$
Siri har likningen:
$a^2=8^2+x^2-8x$
hvilket må bety at
$2 cos A = 1$
$cos A = \frac{1}{2}$
$A=60^o$
Bruker en glider for a i Geogebra, og bruker CAS til å regne ut mulige verdier av x (linje 1 i CAS). Bruker grafikkfeltet til å tegne de ulike trekantene. Ser av linje 2 i CAS at a (n i linje 2) må være minst 7 for at vi skal få en trekant som tilfredsstiller likningen. For eksempel:
Er a = 8, får vi en likesidet trekant.
Vi har mange mulige trekanter, videre, f.eks: