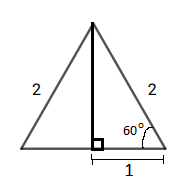Forskjell mellom versjoner av «1T 2023 høst LØSNING»
| Linje 50: | Linje 50: | ||
Nullpunktene til f(x) er x=-3, x=-1 og x=2, og det er i disse punktene grafen til funksjonen skjærer x-aksen. | Nullpunktene til f(x) er x=-3, x=-1 og x=2, og det er i disse punktene grafen til funksjonen skjærer x-aksen. | ||
| + | |||
| + | ==Oppgave 3== | ||
| + | |||
| + | ==Oppgave 4== | ||
| + | |||
| + | ==Oppgave 5== | ||
=DEL 2= | =DEL 2= | ||
Revisjonen fra 23. nov. 2023 kl. 08:04
DEL 1
Oppgave 1
Siden trekanten er likesidet, er alle vinklene like store. Hver vinkel er $180 : 3 = 60$ grader.
Jeg tegner inn høyden i trekanten, slik at jeg får en rettvinklet trekant, med hypotenus med lengde 2, og hosliggende katet til 60-gradersvinkelen med lengde 1 (se figur).
Jeg bruker definisjonen til cosinus av en vinkel i et rettvinklet trekant: cos v = hosliggende katet / hypotenus
Vi har at:
$cos \, 60^o = \frac{1}{2}$
Oppgave 2
Vi har $f(x)=x^3+2x^2-5x-6$
Siden f er en tredjegradsfunksjon, forventer jeg å finne opptil 3 nullpunkter. Jeg prøver meg frem med noen x-verdier, og finner at x = 2 er et nullpunkt, her vist ved regning:
$f(2)=2^3+2\cdot 2^2-5\cdot2-6=8+8-10-6=0$
Jeg utfører polynomdivisjonen f(x):(x-2) for å kunne finne de andre nullpunktene.
$\quad(x^3+2x^2-5x-6):(x-2)=x^2+4x+3$
$-(x^3-2x^2)$
$\quad \quad \quad 4x^2-5x-6$
$\quad\quad-(4x^2-8x)$
$\quad\quad\quad\quad\quad\quad3x-6$
$\quad\quad\quad\quad\quad-(3x-6)$
$\quad\quad\quad\quad\quad\quad\quad\quad0$
Jeg finner nullpunktene til andregradsuttrykket, ved å bruke abc-formelen:
$x^2+4x+3 = 0$
$x=\frac{-4\pm\sqrt{4^2-4\cdot1\cdot3}}{2\cdot 1}$
$x=\frac{-4\pm2}{2}$
$x_1=-3$ v $x_2=-1$
Nullpunktene til f(x) er x=-3, x=-1 og x=2, og det er i disse punktene grafen til funksjonen skjærer x-aksen.
Oppgave 3
Oppgave 4
Oppgave 5
DEL 2
Oppgave 1
a)
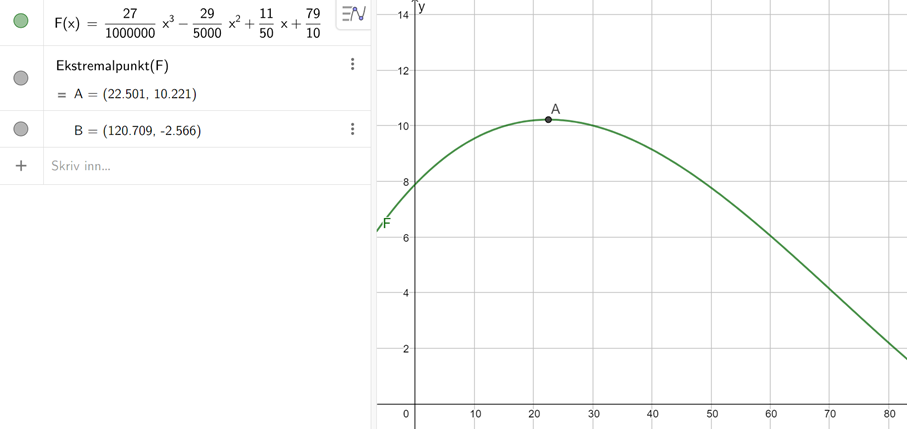
Metode 1: finne ekstremalpunktene ved å finne x-verdiene hvor den deriverte er lik 0. Det er kun én verdi innenfor definisjonsområdet. Sjekker om dette er et toppunkt, ved å sjekke at funksjonen vokser like før ekstremalpunktet, og synker like etter ekstremalpunktet.
Metode 2: Grafisk, ved å tegne grafen til F, og finne ekstremalpunktene. Det er da synlig at det er ett toppunkt i definisjonsområdet.
Høyeste folketall: 22.5 år etter 1960, altså i 1982.
b)
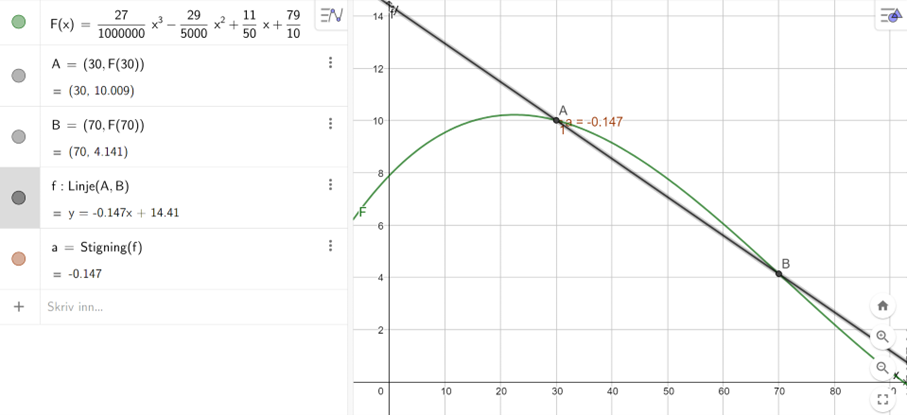
Tegner punktene A=(30,F(30)) og B=(70,F(70)) i Geogebra, tegner linjen som går gjennom punktene, og finner stigningen til linjen.
Stigningstallet er -0,147 tusen mennesker/år, som vil si at mellom 1990 og 2030, avtar folketallet gjennomsnittlig med 147 mennesker per år.
c)
Tegner grafen til F’(x), og finner bunnpunktet til denne (se punkt C).
Vi ser at F’ har lavest verdi for x=71.6, det vil si at folketallet avtar raskest i 2031.
Oppgave 2
1. Bruker cosinussetningen for å finne vinkel C.
2. Bruker arealsetningen for å finne arealet til trekant BCD.
3. Bruker sinussetningen for å finne lengden AB. Vinkel BDA er 180-125-35=20 grader.
4. Bruker arealsetningen for å finne arealet til trekan ABD.
5. Legger sammen arealet til trekantene, og finner arealet til ABCD.
Oppgave 3
a)
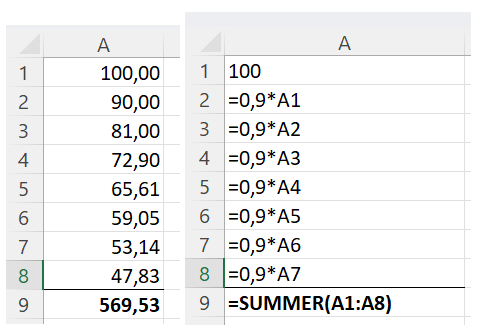
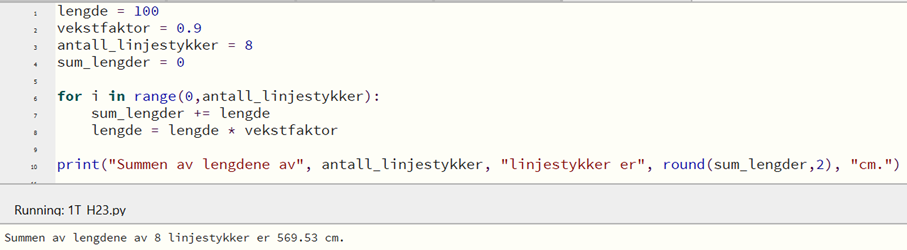
Bruker Excel til å finne lengden på de 8 første linjestykkene, og summerer deretter lengden på disse linjestykkene.
Summen av lengden av de 8 første linjestykkene er 569,5 cm.
b)
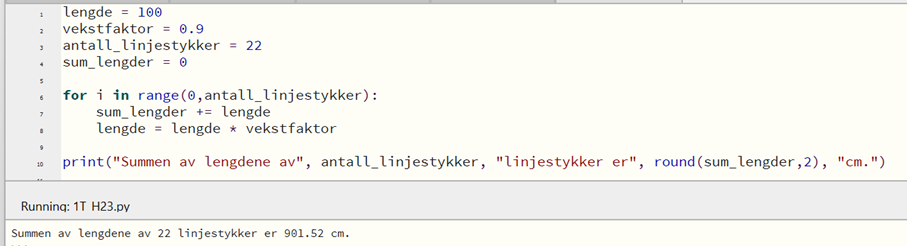
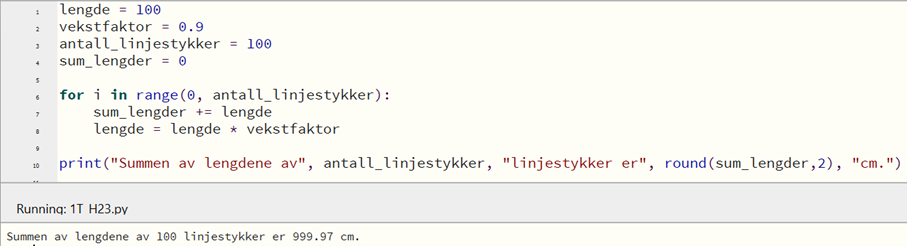
Jeg kan argumentere for at formler i Excel løser oppgaven, men jeg viser her programmering i Python, hvor jeg kan angi antall linjestykker selv:
For å finne hvor mange linjestykker figuren må ha, for at summen av lengdene skal være minst 9 meter (900 cm), kan jeg prøve meg frem med antall linjestykker i programmet. Jeg finner at 22 linjestykker gir en sum på over 900 cm.
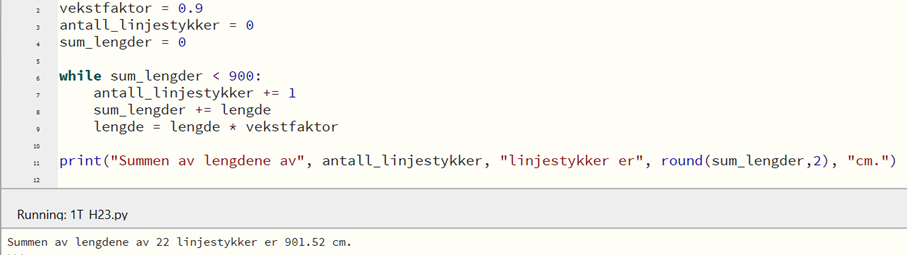
En bedre metode, hvor jeg ikke må prøve meg frem, er å bruke en while-løkke i stedet:
c)
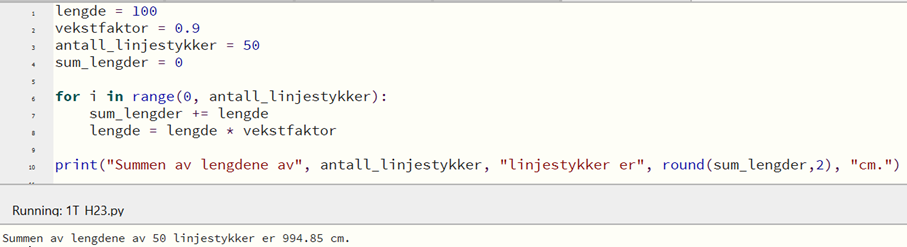
Bruker det første programmet mitt til å regne ut summen av lengdene til henholdsvis 50 og 100 linjestykker.
Regner ut hvor mange prosent forskjell det er for summen av lengdene:
$\frac{999,97 – 994,85}{994,85} \cdot 100 \% = 0,51 \% $
Det er ca. 0,51 % økning i summen av lengdene, dersom vi øker antall linjestykker i figuren fra 50 til 100.