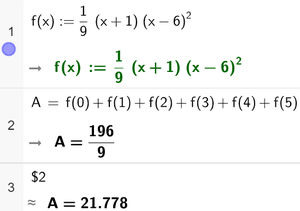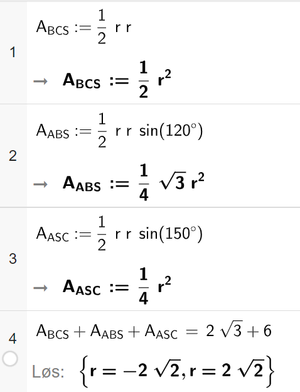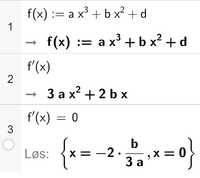1T 2023 vår LK20 LØSNING

Oppgaven som pdf

Diskusjon av oppgaven på matteprat

DEL 2

Oppgave 4

a)

Arealet av hvert rektangel er gitt ved:

$A=l\cdot b = 1\cdot f(x)$

Bruker CAS til å regne ut summen til arealet av de seks rektanglene.

Arealet er av de seks rektanglene er ca. 21,8.

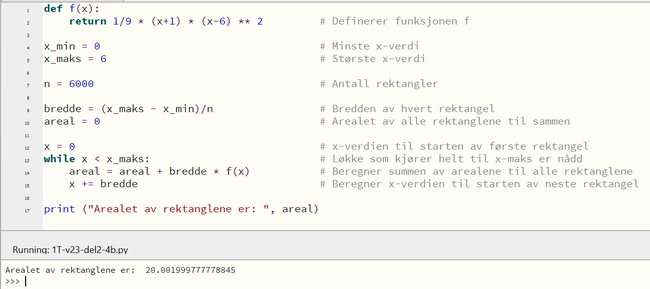
b) og c)

Arealet av 6000 rektangler er ca. 20.

Oppgave 5

Løser oppgaven i CAS. Finner arealet av hver trekant uttrykt ved r (linje 1-3), og løser til slutt likningen for summen av arealene til de tre trekantene (linje 4) for å finne verdien til r.

Linje 1: bruker formelen for areal av en trekant, A = 1/2 * grunnlinje * høyde

Linje 2: arealsetningen. $\angle{ASB}= 180^{\circ}-30^{\circ}-30^{\circ} = 120^{\circ}$

Linje 3: arealsetningen. $\angle{ASC}= 360^{\circ}-90^{\circ}-120^{\circ} = 150^{\circ}$

Verdien av r er $2\sqrt{2}$.

Oppgave 6

a)

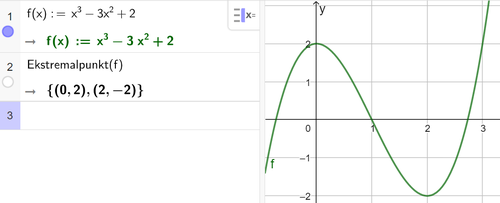
Bruker CAS til å bestemme topp- og bunnpunktene, og ser på grafen at dette er topp- og bunnpunkt (og f.eks. ikke terrassepunkt).

Grafen til f har et toppunkt i (0,2) og et bunnpunkt i (2,-2).

b)

Hvis man tegner en generell tredjegradsfunksjon uten førstegradsledd i Geogebra, $f(x)=ax^3+bx^2+d$, og bruker glidere for a, b, og d, vil man se at det alltid er et topp-, bunn-, eller terrassepunkt i x = 0. For eksempel har grafen til $x^3$ et terrassepunkt i x = 0.

Dersom man deriverer denne generelle tredjegradsfunksjon uten førstegradsledd, f, ser man at den deriverte alltid er lik 0 når x = 0. Det vil si at grafen til f har et topp- bunn- eller terrassepunkt i x = 0, for alle verdier av a, b og d. Et eventuelt annet ekstremalpunktet vil avhenge av verdien til a og b. Jeg bruker CAS for å vise dette: