2P 2019 vår LØSNING: Forskjell mellom sideversjoner
Ny side: [https://matematikk.net/matteprat/download/file.php?id=2413 Oppgaven som pdf] [https://matematikk.net/matteprat/viewtopic.php?f=13&t=49196 Diskusjon av denne oppgaven] |
|||
| (56 mellomliggende versjoner av 2 brukere er ikke vist) | |||
| Linje 1: | Linje 1: | ||
[https://matematikk.net/matteprat/download/file.php?id=2413 Oppgaven som pdf] | [https://matematikk.net/matteprat/download/file.php?id=2413 Oppgaven som pdf] | ||
[https://matematikk.net/matteprat/download/file.php?id=2435 Løsningsforslag laget av Marius Nilsen ved Bergen Private Gymnas] | |||
[https://matematikk.net/matteprat/viewtopic.php?f=13&t=49196 Diskusjon av denne oppgaven] | [https://matematikk.net/matteprat/viewtopic.php?f=13&t=49196 Diskusjon av denne oppgaven] | ||
===DEL EN=== | |||
==Oppgave 1== | |||
Organiserer datamaterialet i stigende rekkefølge: | |||
0,0, 1,1,1,1, 2,2,2,2,2, 3,3,3, 4, 5,5, 6, 8, 9 | |||
Variasjonsbredden er største minus minste verdi: 9 - 0 = 9 | |||
Median er gjennomsnittet av de to tallene i midten (fordi antall verdier er partall): 2 | |||
Gjennomsnittet er summen delt på antall observasjoner: $\frac{60}{20} = 3$ | |||
==Oppgave 2== | |||
$0,8x = 640 \\ x = \frac{640}{0,8} \\ x = 800$ | |||
Varen kostet 800 kroner. | |||
==Oppgave 3== | |||
$7,03 \cdot 10^7 - 7000000 = \\ 7,03 \cdot 10^7 - 0,7 \cdot 10^7 = \\ (7,03- 0,7) \cdot 10^7 = \\ 6,33 \cdot 10^7$ | |||
==Oppgave 4== | |||
$\frac{2^0+2^3 \cdot 2^2 + (2^3)^2 - 2}{2 \cdot 2^2} +2^{-3} = \\ \frac{1+8\cdot 4+ 64-2}{8} + \frac 18 = \\ \frac{95}{8} + \frac 18 = \\ \frac{96}{8} = 12$ | |||
==Oppgave 5== | |||
a) | |||
y = ax + b, der a er stigningstall og b er skjæring med y akse (konstantledd). Vi ser at grafen øker med 200 når antallet pakker øker fra 4 til 8. Det betyr at a = 50. | |||
Vi har at: | |||
$350 = 50 \cdot 4 + b \\ b = 150 $ | |||
Altså y = 50x + 150 | |||
==b)== | |||
Det koster 50 kroner per pakke (stigningstall a). x er antall pakker. Det koster 150 kroner for å få budfirmaet til å møte opp (konstantledd b), altså en fast kostnad. | |||
==Oppgave 6== | |||
===a)=== | |||
Når man skal regne gjennomsnitt i klassedelt materiale antar vi at gjennomsnittet i hver klasse ligger på klassemidpunktet, selv om vi egentlig ikke vet noe om det. Det viser seg at dette ofte blir ganske riktig. | |||
Klaaemidpunktene er: 5, 15, 30 og 60. | |||
Vi multipliserer disse med den tilhørende frekvensen, legger sammen resultatene for alle klassene ( her er det fire) og deler på det totale antall (200): | |||
$Gjsnitt = \frac{5 \cdot 60 + 15 \cdot 80 + 30 \cdot 50 + 60 \cdot 10}{200} = \frac{300 + 1200 + 1500 + 600}{200} = \frac{3600}{200} = 18$ | |||
Gjennomsnittlig reisetid er ca. 18 minutter. | |||
===b)=== | |||
Når det er 200 elever, er medianeleven gjennomsnittet av elev 100 og 101, altså cirka 40 elever inn i klasse [10, 20>. Dette er midt i klassen, siden den har 80 elementer. I Stigende rekkefølge, jevnt fordelt, blir medianverdien ca 15 minutter, som også er klassemidtpunkt. | |||
===c)=== | |||
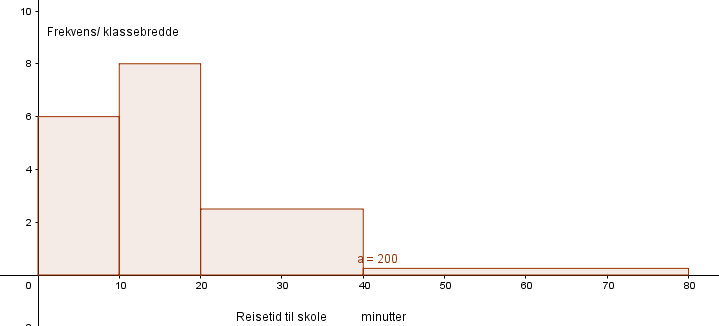
Du må gjøre dette med blyant og linjal. Husk at "søylehøyden" er frekvens delt på klassebredde. | |||
[[File:2p-v19-1-6-c.png]] | |||
==Oppgave 7== | |||
===a)=== | |||
[[File:2p-v19-1-7-a.png]] | |||
===b)=== | |||
[[File:2p-v19-1-7-b.png]] | |||
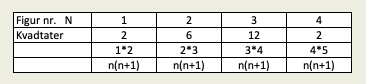
Ved å bruke de små kvadratene til å lage ett stort ser man at man hele tiden får ett lite kvadrat til overs, altså $n^2 + 1$ | |||
===c)=== | |||
[[File:2p-v19-1-7-c.png]] | |||
Antall kvadrater i figur nr. n kan uttrykkes som $A(n) = n^2 + n$. | |||
==DEL TO== | |||
==Oppgave 1== | |||
===a)=== | |||
$V(x)= (10-0,1x^2)^3 \quad 0\leq x \leq 10$ | |||
$V(0) = 10^3 = 1000$ | |||
Tanken rommer 1000 liter. | |||
===b)=== | |||
[[File:2p-v19-2-1-b.png]] | |||
===c)=== | |||
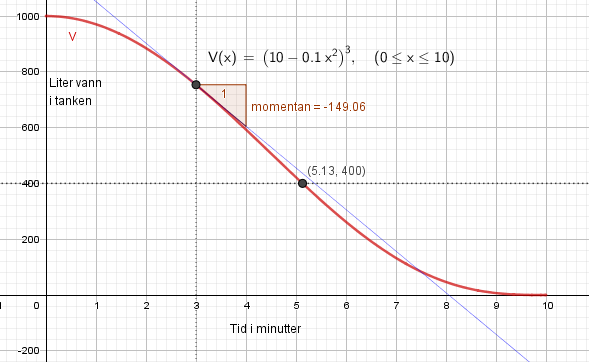
Fra figuren i b ser man at det tar 5,13 minutter i desimal tid. Vi gjør 0,13 om til sekunder: | |||
$\frac{13}{100} =\frac {x}{60} \\ x =7,8$ | |||
Det tar 5 minutter og 8 sekunder før det er 400 liter igjen i tanken. | |||
===d)=== | |||
1000 liter tømmes på 10 minutter. Det blir i gjennomsnitt 1000 liter/ 10 min som er 100 L/min. | |||
===e)=== | |||
Se figuren i b: Lag linjen x=3 og finn skjæring med grafen. I punktet lager man tangenten til grafen. Stigningen til tangenten i punktet er den momentane veksten for x =3. Den er - 149. Det betyr at akkurat når det har gått 3 minutter tømmes tanken med en fart på 149 L/ min. | |||
==Oppgave 2== | |||
==Oppgave 3== | |||
===a)=== | |||
5,3 millioner = 5 300 000 = $ 5,3 \cdot 10^6$ | |||
Dette er en litt uklar oppgave, men her antar man at det er plasten i en vegg som er 0,035mm, da blir tykkelsen av en pose 0,070 mm. | |||
180 poser med en høyde på 0,07 mm = 0,00007 meter = $7,0 \cdot 10^{-5}$ | |||
Høyde: $h =7,0 \cdot 10^{-5} \cdot 5,3 \cdot 10^6 \cdot 180 m = 66780$ meter. | |||
===b)=== | |||
Det er $365 \cdot 24= 8760$ timer i et år. Vi finner hvor mange meter poser som kastes per time i gjennomsnitt: 66740m / 8760 timer = 7,6m/t. Dersom man stabler plastposene oppå hverandre kastet det en stabel på 7,6 meter hver time, i gjennomsnitt. Tar man høyden på Eiffeltårnet og deler på 7,6 m/t finner man hvor mange timer det vil ta før stabelen er like høy som tårnet. | |||
324m : 7,6 m/t = 42,6 | |||
Det tar ca. 43 timer, altså under to døgn, før stabelen er like høy som Eiffeltårnet. | |||
==Oppgave 4== | |||
===a)=== | |||
[[File:2p-v19-2-4-a.png]] | |||
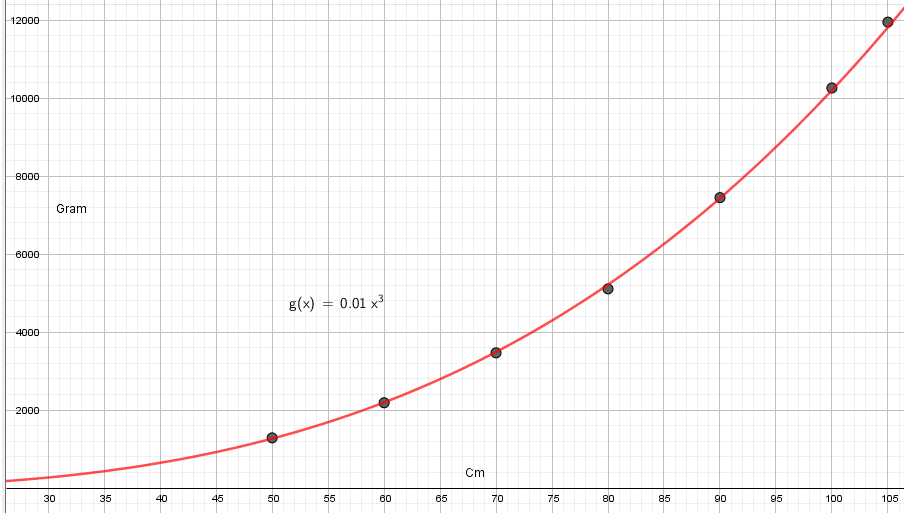
Bruker regresjon i Geogebra. a = 0,01 og b = 3. | |||
===b)=== | |||
Vi bruker vekstfaktor. 25% tilsvarer vekstfaktor 1,25. $1,25^3 = 1,95$ som tilsvarer 95% eller nesten en dobling. Når lengden øker med 25% får vi nesten en dobling (95%) av vekten. | |||
==Oppgave 5== | |||
===a)=== | |||
Utgangsprisen er 800 kr. For hver time som går, halveres prisen. Halvparten av 50 kr. er 25 kr. og halvparten av det er 12,50. Dvs. kl 02:00 er prisen 13 kroner (50 øren er historie). | |||
===b)=== | |||
Dette er en verdi som reduseres med 50% hver time: $f(x) = 800 \cdot 0,5^x$. Vekstfaktoren er 0,5 og x er tiden i timer. | |||
==Oppgave 6== | |||
===a) | |||
===b)=== | |||
=== 1=== | |||
Er ikke mulig. Da burde gjennomsnittet i Idas poser være større enn Emils. | |||
===2=== | |||
Det er ikke mulig for da ville standardavviket være null. | |||
===3=== | |||
Det kan være mulig. Da er det stor spredning på resterende poser. | |||
==Oppgave 7== | |||
'''Situasjon 1:''' | |||
Dette er en lineær sammenheng. 9 kroner er konstantleddet, og stigningstallet er 15 kroner. x er antall hektogram. Kurve H beskriver situasjonen. | |||
'''Situasjon 2''' | |||
Når en størrelse vokser med en fast prosent, vil det si at den vokser eksponentielt. Graf B beskriver forløpet. | |||
'''Situasjon 3''' | |||
Et eksempel på at det lønner seg å følge med i naturfagtimene også :-) Når noe først vokser tilnærmet eksponentielt, for så å stabilisere seg har man det man i naturfag kaller sigmoid vekst som beskrives med en såkalt S kurve. I matematikken kalles dette for logistisk modell. Den kurven som passer best er graf F. | |||
'''Situasjon 4''' | |||
Vi tenker på prisen det koster å sende pakke som y verdien. Vi ser at det kun er tre forskjellige verdier som ikke er kontinuerlige. Hver av prisene gjelder innen et vekt intervall. Graf C passer. | |||
Siste sideversjon per 10. nov. 2020 kl. 22:46
Løsningsforslag laget av Marius Nilsen ved Bergen Private Gymnas
DEL EN
Oppgave 1
Organiserer datamaterialet i stigende rekkefølge:
0,0, 1,1,1,1, 2,2,2,2,2, 3,3,3, 4, 5,5, 6, 8, 9
Variasjonsbredden er største minus minste verdi: 9 - 0 = 9
Median er gjennomsnittet av de to tallene i midten (fordi antall verdier er partall): 2
Gjennomsnittet er summen delt på antall observasjoner: $\frac{60}{20} = 3$
Oppgave 2
$0,8x = 640 \\ x = \frac{640}{0,8} \\ x = 800$
Varen kostet 800 kroner.
Oppgave 3
$7,03 \cdot 10^7 - 7000000 = \\ 7,03 \cdot 10^7 - 0,7 \cdot 10^7 = \\ (7,03- 0,7) \cdot 10^7 = \\ 6,33 \cdot 10^7$
Oppgave 4
$\frac{2^0+2^3 \cdot 2^2 + (2^3)^2 - 2}{2 \cdot 2^2} +2^{-3} = \\ \frac{1+8\cdot 4+ 64-2}{8} + \frac 18 = \\ \frac{95}{8} + \frac 18 = \\ \frac{96}{8} = 12$
Oppgave 5
a)
y = ax + b, der a er stigningstall og b er skjæring med y akse (konstantledd). Vi ser at grafen øker med 200 når antallet pakker øker fra 4 til 8. Det betyr at a = 50.
Vi har at:
$350 = 50 \cdot 4 + b \\ b = 150 $
Altså y = 50x + 150
b)
Det koster 50 kroner per pakke (stigningstall a). x er antall pakker. Det koster 150 kroner for å få budfirmaet til å møte opp (konstantledd b), altså en fast kostnad.
Oppgave 6
a)
Når man skal regne gjennomsnitt i klassedelt materiale antar vi at gjennomsnittet i hver klasse ligger på klassemidpunktet, selv om vi egentlig ikke vet noe om det. Det viser seg at dette ofte blir ganske riktig.
Klaaemidpunktene er: 5, 15, 30 og 60.
Vi multipliserer disse med den tilhørende frekvensen, legger sammen resultatene for alle klassene ( her er det fire) og deler på det totale antall (200):
$Gjsnitt = \frac{5 \cdot 60 + 15 \cdot 80 + 30 \cdot 50 + 60 \cdot 10}{200} = \frac{300 + 1200 + 1500 + 600}{200} = \frac{3600}{200} = 18$
Gjennomsnittlig reisetid er ca. 18 minutter.
b)
Når det er 200 elever, er medianeleven gjennomsnittet av elev 100 og 101, altså cirka 40 elever inn i klasse [10, 20>. Dette er midt i klassen, siden den har 80 elementer. I Stigende rekkefølge, jevnt fordelt, blir medianverdien ca 15 minutter, som også er klassemidtpunkt.
c)
Du må gjøre dette med blyant og linjal. Husk at "søylehøyden" er frekvens delt på klassebredde.
Oppgave 7
a)
b)
Ved å bruke de små kvadratene til å lage ett stort ser man at man hele tiden får ett lite kvadrat til overs, altså $n^2 + 1$
c)
Antall kvadrater i figur nr. n kan uttrykkes som $A(n) = n^2 + n$.
DEL TO
Oppgave 1
a)
$V(x)= (10-0,1x^2)^3 \quad 0\leq x \leq 10$
$V(0) = 10^3 = 1000$
Tanken rommer 1000 liter.
b)
c)
Fra figuren i b ser man at det tar 5,13 minutter i desimal tid. Vi gjør 0,13 om til sekunder:
$\frac{13}{100} =\frac {x}{60} \\ x =7,8$
Det tar 5 minutter og 8 sekunder før det er 400 liter igjen i tanken.
d)
1000 liter tømmes på 10 minutter. Det blir i gjennomsnitt 1000 liter/ 10 min som er 100 L/min.
e)
Se figuren i b: Lag linjen x=3 og finn skjæring med grafen. I punktet lager man tangenten til grafen. Stigningen til tangenten i punktet er den momentane veksten for x =3. Den er - 149. Det betyr at akkurat når det har gått 3 minutter tømmes tanken med en fart på 149 L/ min.
Oppgave 2
Oppgave 3
a)
5,3 millioner = 5 300 000 = $ 5,3 \cdot 10^6$
Dette er en litt uklar oppgave, men her antar man at det er plasten i en vegg som er 0,035mm, da blir tykkelsen av en pose 0,070 mm.
180 poser med en høyde på 0,07 mm = 0,00007 meter = $7,0 \cdot 10^{-5}$
Høyde: $h =7,0 \cdot 10^{-5} \cdot 5,3 \cdot 10^6 \cdot 180 m = 66780$ meter.
b)
Det er $365 \cdot 24= 8760$ timer i et år. Vi finner hvor mange meter poser som kastes per time i gjennomsnitt: 66740m / 8760 timer = 7,6m/t. Dersom man stabler plastposene oppå hverandre kastet det en stabel på 7,6 meter hver time, i gjennomsnitt. Tar man høyden på Eiffeltårnet og deler på 7,6 m/t finner man hvor mange timer det vil ta før stabelen er like høy som tårnet.
324m : 7,6 m/t = 42,6
Det tar ca. 43 timer, altså under to døgn, før stabelen er like høy som Eiffeltårnet.
Oppgave 4
a)
Bruker regresjon i Geogebra. a = 0,01 og b = 3.
b)
Vi bruker vekstfaktor. 25% tilsvarer vekstfaktor 1,25. $1,25^3 = 1,95$ som tilsvarer 95% eller nesten en dobling. Når lengden øker med 25% får vi nesten en dobling (95%) av vekten.
Oppgave 5
a)
Utgangsprisen er 800 kr. For hver time som går, halveres prisen. Halvparten av 50 kr. er 25 kr. og halvparten av det er 12,50. Dvs. kl 02:00 er prisen 13 kroner (50 øren er historie).
b)
Dette er en verdi som reduseres med 50% hver time: $f(x) = 800 \cdot 0,5^x$. Vekstfaktoren er 0,5 og x er tiden i timer.
Oppgave 6
===a)
b)
1
Er ikke mulig. Da burde gjennomsnittet i Idas poser være større enn Emils.
2
Det er ikke mulig for da ville standardavviket være null.
3
Det kan være mulig. Da er det stor spredning på resterende poser.
Oppgave 7
Situasjon 1:
Dette er en lineær sammenheng. 9 kroner er konstantleddet, og stigningstallet er 15 kroner. x er antall hektogram. Kurve H beskriver situasjonen.
Situasjon 2
Når en størrelse vokser med en fast prosent, vil det si at den vokser eksponentielt. Graf B beskriver forløpet.
Situasjon 3
Et eksempel på at det lønner seg å følge med i naturfagtimene også :-) Når noe først vokser tilnærmet eksponentielt, for så å stabilisere seg har man det man i naturfag kaller sigmoid vekst som beskrives med en såkalt S kurve. I matematikken kalles dette for logistisk modell. Den kurven som passer best er graf F.
Situasjon 4
Vi tenker på prisen det koster å sende pakke som y verdien. Vi ser at det kun er tre forskjellige verdier som ikke er kontinuerlige. Hver av prisene gjelder innen et vekt intervall. Graf C passer.