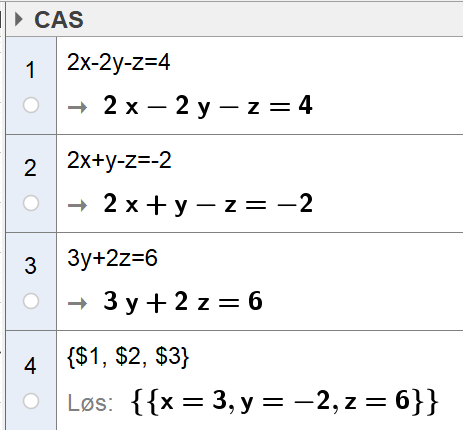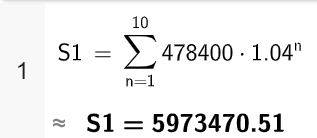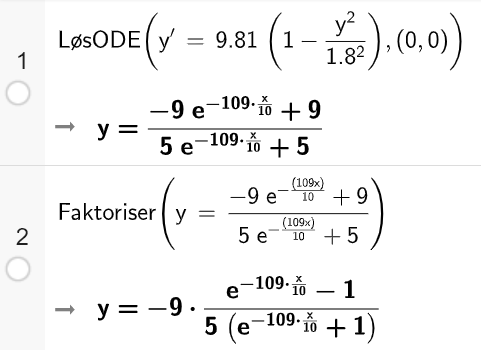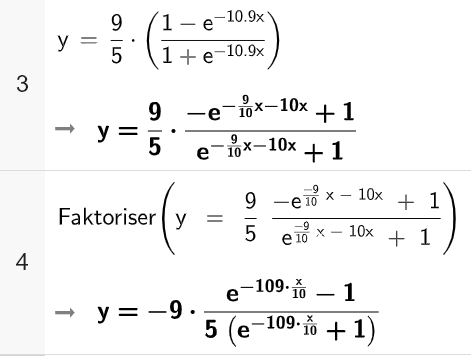R2 2019 høst LØSNING: Forskjell mellom sideversjoner
Ingen redigeringsforklaring |
|||
| (58 mellomliggende versjoner av 3 brukere er ikke vist) | |||
| Linje 8: | Linje 8: | ||
[https://matematikk.net/matteprat/download/file.php?id=2710 Løsningsforslag laget av Ole Henrik Morgenstierne] | [https://matematikk.net/matteprat/download/file.php?id=2710 Løsningsforslag laget av Ole Henrik Morgenstierne] | ||
[https://www.youtube.com/playlist?list=PLplkS_rtcCHVqAzWxwetJfU5F0o6GDze4 Løsning til del 1 som videoer laget av Lektor Håkon Raustøl] | |||
[https://m.youtube.com/playlist?list=PLplkS_rtcCHWRqVt1H1n759heFzppOBfk Løsning til del 2 som videoer laget av Lektor Håkon Raustøl] | |||
=DEL 1= | |||
==Oppgave 1== | |||
===a)=== | |||
$f(x)=2cos(\pi x)$ | |||
$f'(x)=-2 \pi sin(\pi x)$ | |||
===b)=== | |||
$g(x)=cos^2 x \cdot sin\, x$ | |||
$g'(x)=(cos^2 x)' \cdot sin\, x + cos^2 x \cdot (sin\, x)' \\ = 2cos\, x \cdot (-sin\, x) \cdot sin\, x + cos^2 x \cdot cos\, x \\ = -2sin^2 x \cdot cos x + cos^3 x$ | |||
==Oppgave 2== | |||
===a)=== | |||
$\int_{-1}^{1} (2x^3+3x-1) dx \\ = [ \frac{2}{4}x^4+\frac{3}{2}x^2-x]_{-1}^{1} \\ =(\frac{1}{2}\cdot 1^4+\frac{3}{2}\cdot 1^2-1)-(\frac{1}{2}\cdot (-1)^4+\frac{3}{2}\cdot (-1)^2-(-1)) \\ =(\frac{1}{2}+\frac{3}{2}-1)-(\frac{1}{2}+\frac{3}{2}+1) \\ = -1-1 = -2$ | |||
===b)=== | |||
$u=2x^2-1$ | |||
$\frac{du}{dx}=4x \Rightarrow dx=\frac{du}{4x}$ | |||
$\int \frac{8x}{\sqrt{2x^2-1}} dx = \int \frac{8x}{\sqrt{u}} \cdot \frac{du}{4x} = \int \frac{2}{\sqrt{u}} du = 2 \int u^{-\frac{1}{2}} du \\ = \frac{2}{\frac{1}{2}}\cdot u^{\frac{1}{2}} + C = 4 \cdot \sqrt{u} + C = 4\sqrt{2x^2-1}+C$ | |||
===c)=== | |||
$\int \frac{2}{(x+3)(x+1)}dx = \int \frac{A}{(x+3)}+\frac{B}{(x+1)} dx $ | |||
Vi bestemmer A og B ved å løse likningen: | |||
$2 = (x+1)A + (x+3)B \\ 2=Ax+A+Bx+3B \\ 2=(A+B)x + A+ 3B$ | |||
Telleren har ikke noe x-ledd, så vi har: | |||
I $A+B=0$ | |||
II$A+3B=2$ | |||
Setter inn $A=-B$ i likning II: | |||
$-B+3B=2 \Rightarrow B=1$ | |||
Fra likning I har vi da $A=-1$ | |||
Integralet blir da: | |||
$\int \frac{2}{(x+3)(x+1)}dx = \int \frac{A}{(x+3)}+\frac{B}{(x+1)} dx = \int \frac{-1}{(x+3)}+\frac{1}{(x+1)} dx \\ = - \ln|{x+3}| + \ln|{x+1}| + C = \ln|{\frac{x+1}{x+3}}| + C$ | |||
==Oppgave 3== | |||
===a)=== | |||
Summen av en aritmetisk rekke er gitt ved | |||
$S_n=\frac{n\cdot (a_1+a_n)}{2}$ | |||
Vi må finne antall ledd i rekken $7+11+....+479+483$. | |||
Ser at $d=4$, så antall ledd (n) blir: | |||
$n=\frac{483-7}{4}+1=\frac{476}{4}+1=119+1=120$ | |||
Summen av denne rekken blir: | |||
$S_{120}=\frac{120\cdot (7+483)}{2}= 60\cdot(7+483)=420+28980 =29400$ | |||
===b)=== | |||
For en geometrisk rekke har vi | |||
$a_n=a_1\cdot k^{n-1}$ | |||
Vi vet at $a_2=6$ og får likning I: | |||
$a_2=a_1\cdot k^{2-1} \\ 6=a_1\cdot k \\ a_1=\frac{6}{k}$ | |||
Summen av en geometrisk rekke som konvergerer er gitt ved | |||
$S=\frac{a_1}{(1-k)}$ | |||
Vi vet at summen av rekken er 24 og har dermed likning II: | |||
$24=\frac{a_1}{(1-k)} \\ a_1=24(1-k)$ | |||
Setter inn $a_1=\frac{6}{k}$ i likning II: | |||
$\frac{6}{k} = 24(1-k) \\ 6=24k(1-k) \\ 6=24k-24k^2 \\ 24k^2-24k+6=0 \\ k^2-k+\frac{1}{4}=0 \\ (k-\frac{1}{2})(k-\frac{1}{2})=0 \\ k=\frac{1}{2} $ | |||
Setter inn $k=\frac{1}{2} $ i likning I: | |||
$a_1=\frac{6}{\frac{1}{2}}=12$ | |||
==Oppgave 4== | |||
===a)=== | |||
$2sin(2x)=1$, der $x\in[0,\pi]$ | |||
$sin(2x)=\frac{1}{2}$ | |||
$ 2x=\frac{\pi}{6} + k \cdot 2 \pi \vee 2x = (\pi - \frac{\pi}{6}) + k\cdot 2\pi \quad \quad k \in \mathbb{Z} $ | |||
$ x = \frac{\pi}{12} \vee x = \frac{5\pi}{12} \quad $ kun disse to løsningene gir $x\in[0,\pi]$ | |||
$ L = \{ \frac{\pi}{12}, \frac{5\pi}{12} \}$ | |||
===b)=== | |||
$2cos^2 x-cos x=1$, der $x\in[0,4\pi]$ | |||
$u=cos\,x$ | |||
$2u^2-u-1=0 \\ u^2-\frac{1}{2} u - \frac{1}{2}=0 \\ (u+\frac{1}{2})(u-1)=0 \\ u=-\frac{1}{2} \vee u=1 \\ cos\,x=-\frac{1}{2} \vee cos\, x=1$ | |||
$cos\,x=-\frac{1}{2} \Rightarrow x=\frac{2\pi}{3} + k\cdot 2\pi \Rightarrow L=\{ \frac{2\pi }{3}, \frac{8\pi}{3} \} $ for $x\in[0,4\pi]$ | |||
og $cos\,x=-\frac{1}{2} \Rightarrow x= \frac{4\pi}{3} + k\cdot 2\pi \Rightarrow L=\{ \frac{4\pi}{3}, \frac{10\pi}{3} \}$ for $x\in[0,4\pi]$ | |||
$cos\,x=1 \Rightarrow x=0 + k\cdot 2\pi \Rightarrow L=\{0,2\pi,4\pi \}$ for $x\in[0,4\pi]$ | |||
$L=\{ 0,\frac{2\pi}{3},\frac{4\pi}{3},2\pi,\frac{8\pi}{3},\frac{10\pi}{3},4\pi \}$ | |||
==Oppgave 5== | |||
B er grafen til <i>f</i>. | |||
Dette fordi $sin^2(x)=0$ for $x=0, x=\pi$ og $x=2\pi$ i intervallet $x\in[0,2\pi]$. Dette er de samme nullpunktene som for $sin(x)$. | |||
I tillegg er $sin^2(x)=1$ for $x=\frac{\pi}{2}$ og $x=\frac{3\pi}{2}$ i intervallet $x\in[0,2\pi]$ | |||
==Oppgave 6== | |||
===a)=== | |||
$f(x)=x+a, \quad 0\leq x \leq 2, \quad a>0$ | |||
$\int_{0}^{2} f(x) dx = 3$ | |||
$ [ \frac{1}{2} x^2 + ax]_{0}^{2} = 3$ | |||
$(\frac{1}{2}\cdot 2^2+a\cdot 2)-(\frac{1}{2}\cdot 0^2+a\cdot 0) = 3$ | |||
$\frac{4}{2}+2a-0 = 3$ | |||
$2a = 3-2$ | |||
$a=\frac{1}{2}$ | |||
===b)=== | |||
$V=\int_{0}^{2} \pi (f(x))^2 dx$ | |||
$= \pi \int_{0}^{2} (x+a)^2 dx$ | |||
$=\pi \int_{0}^{2} (x^2 + 2ax + a^2) dx$ | |||
$= \pi [\frac{1}{3}x^3 + \frac{2a}{2} x^2 + a^2x]_{0}^{2}$ | |||
$=\pi [(\frac{1}{3}\cdot(2)^3+a\cdot(2)^2 +a^2\cdot 2)-(\frac{1}{3}\cdot(0)^3+a\cdot(0)^2 +a^2\cdot 0)]$ | |||
$=\pi(\frac{8}{3}+4a+2a^2)$ | |||
Setter inn uttrykket for V i likningen: | |||
$V=\frac{98}{3}\pi$ | |||
$\pi(\frac{8}{3}+4a+2a^2) = \frac{98}{3}\pi \quad | : \pi$ | |||
$\frac{8}{3}+\frac{3\cdot4a}{3}+\frac{3\cdot 2a^2}{3}=\frac{98}{3}$ | |||
$\frac{8}{3}+\frac{12a}{3}+\frac{6a^2}{3}=\frac{98}{3} \quad |\cdot 3$ | |||
$6a^2+12a+8-98=0$ | |||
$6a^2+12a-90=0 \quad |:6$ | |||
$a^2+2a-15=0$ | |||
$(a+5)(a-3)=0$ | |||
$a=-5 \vee a=3$ | |||
Forkaster $a=-5$ siden vi må ha $a>0$. Vi har da $a=3$. | |||
==Oppgave 7== | |||
===a)=== | |||
I <i>xz</i>-planet er $y=0$. Setter inn $y=0$ i uttrykket for $y$: | |||
$y=2-t \\ 0=2-t \\ t=2$ | |||
Setter inn $t=2$ i uttrykket for $x$: | |||
$x=1+2t \\ x=1+2\cdot 2 \\ x=5$ | |||
Setter inn $t=2$ i uttrykket for $z$: | |||
$z= 6+t \\ z=6+2 \\ z=8$ | |||
Skjæringspunktet mellom linjen $\ell$ og <i>xz</i>-planet er (5,0,8). | |||
===b)=== | |||
Linjen $\ell$ står vinkelrett på planet $\alpha$, og retningsvektoren til linjen $\ell$ er derfor lik normalvektoren $\vec{n_\alpha}$ til planet $\alpha$. Dermed er skalarproduktet av $\vec{n_\alpha}$ og en vektor i planet, lik 0. | |||
Likningen for planet er derfor gitt ved: | |||
$[a,b,c] \cdot [x-x_0, y-y_0, z-z_0]=0$ | |||
$a(x-x_0)+b(y-y_0)+c(z-z_0)=0$ | |||
Der a,b og c er koordinatene til planets normalvektor, og $x_0,y_0,z_0$ er et punkt i planet. Vi har $\vec{n_\alpha}=[2,-1,1]$ og punktet $P(2,-2,6)$. | |||
$2(x-2)-1\cdot(y-(-2))+1\cdot(z-6)=0 \\ 2x-4-(y+2)+z-6=0 \\ 2x-y+z-4-2-6=0 \\ 2x-y+z-12=0$ | |||
Likningen for planet $\alpha$ er $2x-y+z-12=0$. | |||
===c)=== | |||
Setter inn uttrykkene for x,y og z fra parameterfremstillingen til linjen $\ell$, i likningen for planet $\alpha$: | |||
$2x-y+z-12=0 \\ 2\cdot ( 1+2t ) - (2-t ) + (6+t) - 12 = 0 \\ 2+4t-2+t+6+t-12=0 \\ 6t-6 = 0 \\ t=1$ | |||
Setter inn $t=1$ i uttrykkene for x,y og z fra parameterfremstillingen til linjen $\ell$: | |||
$x= 1+2t = 1+2\cdot 1=3$ | |||
$y = 2-t = 2-1=1$ | |||
$z= 6+t=6+1=7$ | |||
Skjæringspunktet mellom $\alpha$ og $\ell$ er (3,1,7). | |||
==Oppgave 8== | |||
Vi har gitt differensiallikningen: | |||
$y' -2y=x, \quad y(0)=1$ | |||
===a)=== | |||
Integrerende faktor er $e^{-2x}$ | |||
$y' -2y=x$ | |||
$e^{-2x} y' - 2 e^{-2x} y = x e^{-2x} $ | |||
$(e^{-2x}y)'= x e^{-2x}$ | |||
$y e^{-2x} = \int x e^{-2x} dx$ | |||
Bruker delvis integrasjon, der $u=x$, $u'=1$, $v'= e^{-2x}$, $v=-\frac{1}{2}e^{-2x}$ | |||
$y e^{-2x} = x\cdot (-\frac{1}{2}e^{-2x})-\int (-\frac{1}{2}e^{-2x})dx$ | |||
$y e^{-2x} = -\frac{1}{2} x e^{-2x}- (-\frac{1}{2})\cdot(-\frac{1}{2})\cdot e^{-2x}+C$ | |||
$y (x) = -\frac{1}{2} x-\frac{1}{4} + C e^{2x}$ | |||
Vi har $y(0)=1$ | |||
$-\frac{1}{2} \cdot 0-\frac{1}{4} + C e^{2\cdot 0} = 1$ | |||
$0-\frac{1}{4}+C \cdot 1 = 1$ | |||
$C=1+\frac{1}{4}$ | |||
$C=\frac{5}{4}$ | |||
Setter inn verdien for C i likningen for y: | |||
$y(x)=-\frac{1}{2}x-\frac{1}{4}+\frac{5}{4} e^{2x}$ | |||
===b)=== | |||
Finner stigningstallet til tangenten til y i punktet (0,1): | |||
$y'=x+2y \\ y' = 0+2\cdot 1 \\ y'= 2$ | |||
Finner likningen for tangenten til y i punktet (0,1): | |||
$(y-y_1)=a(x-x_1) \\ (y-1)=2(x-0) \\ y=2x+1$ | |||
==Oppgave 9== | |||
Finner lengden av vektorene mellom sentrum av sirklene: | |||
$\vec{AB}=[1-1,2-(-1), 4-0] = [0,3,4]$ | |||
$|\vec{AB}| = \sqrt{0^2+3^2+4^2} = \sqrt{25} = 5$ | |||
$\vec{BC}=[5-1, 1-2, -4-4] = [4,-1,-8]$ | |||
$|\vec{BC}|=\sqrt{4^2+(-1)^2+(-8)^2} = \sqrt{81} = 9$ | |||
$\vec{AC}=[5-1, 1-(-1), -4-0]=[4, 2, -4]$ | |||
$|\vec{AC}|=\sqrt{4^2+2^2+(-4)^2}=\sqrt{36}=6$ | |||
Finner radien $a, b$ og $c$ til hver av kulene: | |||
$I \quad \quad a+b=5 \\ II \quad \, \, \, b+c=9 \\ III \quad a+c=6$ | |||
$I \quad \quad a = 5-b \\ II \quad \, \, \, c=9-b \\ III \quad 5-b+9-b=6 \\ \quad \quad -2b = 6-5-9 \\ \quad \quad \, \, \, b=\frac{-8}{-2}=4 $ | |||
$I \quad \quad a = 5-4=1 \\ II \quad \, \, \, c=9-4 = 5$ | |||
Radien til kulen med sentrum i A er 1, radien til kulen med sentrum i B er 4, radien til kulen med sentrum i C er 5. | |||
==Oppgave 10== | |||
Vi skal vise at $n^3-n$ er delelig med 3 for alle $n \in \N$ | |||
1. Induksjonsgrunnlag: $n=1$ gir $1^3-1 = 0$, som er delelig med 3. | |||
2. Induksjonstrinnet: Vi antar at $n^3-n$ er delelig delelig med 3 når $n=k$. Med $n = k+1$ får vi: | |||
$(k+1)^3-(k+1) \\= (k+1)((k+1)^2-1) \\= (k+1)((k^2+2k+1)-1) \\= (k+1)(k^2+2k) \\=k^3+2k^2+k^2+2k \\=k^3+3k^2+2k \\=k^3+3k^2+2k+k-k\\=k^3-k+3k^2+3k \\= (k^3-k) + 3(k^2+k)$ | |||
$k^3-k$ er delelig med 3, ifølge antakelsen for $n=k$. $3(k^2+k)$ er en faktor av 3, og er derfor delelig med 3. Summen av to ledd som begge er delelig med 3, er også delelig med 3. Vi har vist at $n^3-n$ er delelig med 3 for $n=k+1$. | |||
$n^3-n$ er delelig med 3 for alle $n \in \N$, hvilket skulle vises. | |||
=DEL 2= | |||
==Oppgave 1== | |||
===a)=== | |||
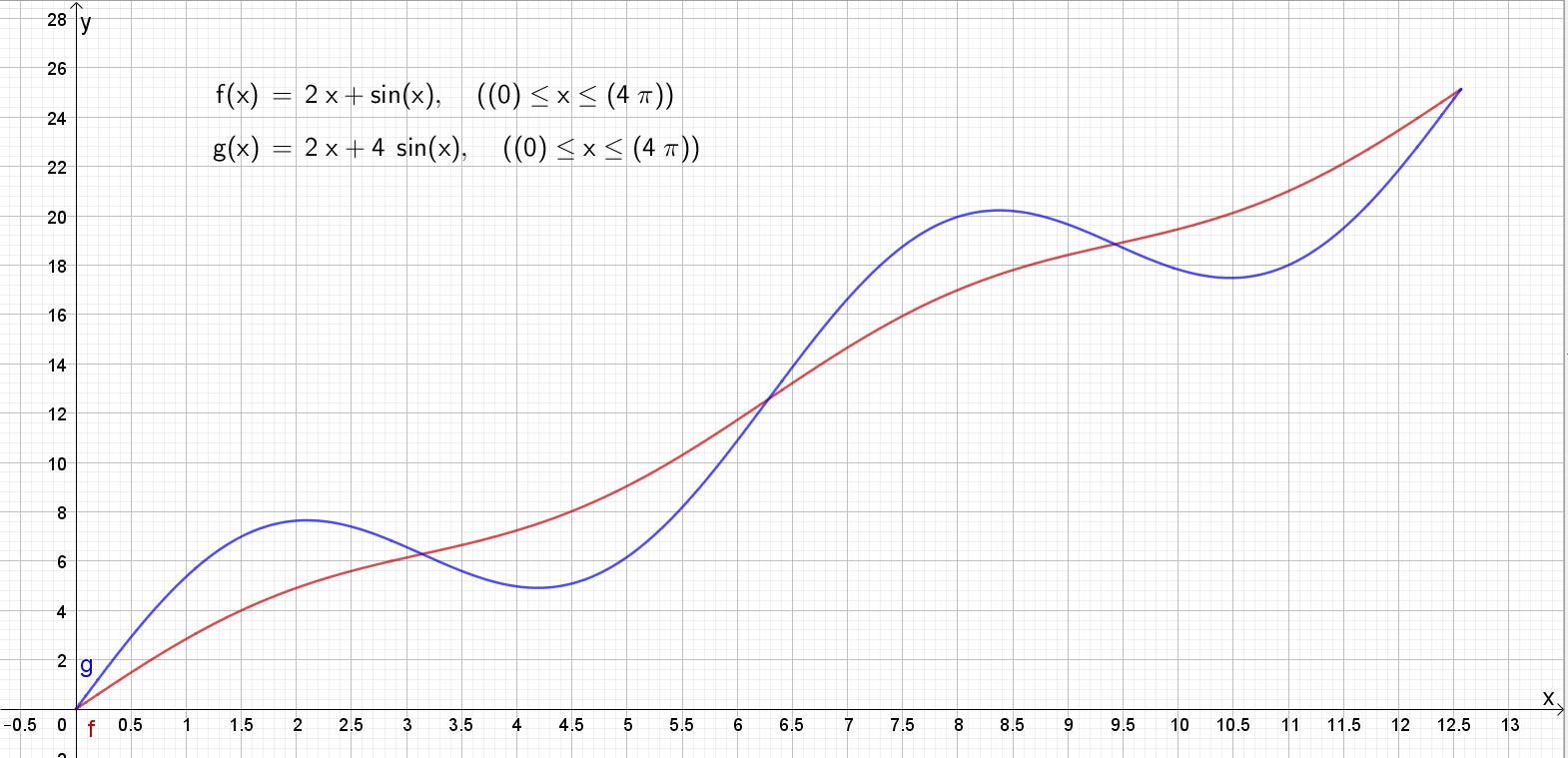
Bruker Geogebra til å tegne grafene til <i>f</i> og <i>g</i> i samme koordinatsystem. | |||
[[File: R2_H19_del2_1a.png]] | |||
===b)=== | |||
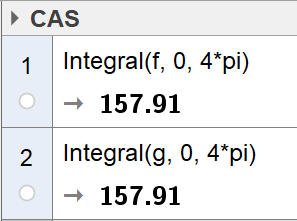
Bruker CAS i Geogebra til å bestemme arealet under grafen til <i>f</i> og arealet under grafen til <i>g</i>. | |||
[[File: R2_H19_del1_1b.png]] | |||
Arealet under grafen til <i>f</i> er 157,91 og arealet under grafen til <i>g</i> er også 157,91. | |||
===c)=== | |||
Bruker CAS i Geogebra til å finne volumet til hvert av de to omdreiingslegemene. | |||
[[File: R2_H19_del1_1c.png]] | |||
Volumet til omdreiingslegemet til <i>f</i> er 8174,07. | |||
Volumet til omdreiingslegemet til <i>g</i> er 7996,42. | |||
===d)=== | |||
Bruker CAS i Geogebra til å vise at arealet til <i>F</i> er uavhengig av k. | |||
[[File: R2_H19_del2_1d.png]] | |||
Vi ser i linje 6 at arealet ikke er avhengig av k, hvilket skulle vises. $16\pi^2$ er for øvrig samme verdi som vi fikk i a). | |||
===e)=== | |||
Bruker CAS til å bestemme hvilken verdi for k som gir minst volum til omdreiingslegemet. | |||
[[File: R2_H19_del2_1e.png]] | |||
$k=4$ gir minst volum. | |||
==Oppgave 2== | |||
===a)=== | |||
Bruker CAS i Geogebra til å finne skjæringspunktet til de tre planene. | |||
[[File: R2_H19_del2_2a.png]] | |||
Planene skjærer hverandre i punktet P(3,-2,6). | |||
===b)=== | |||
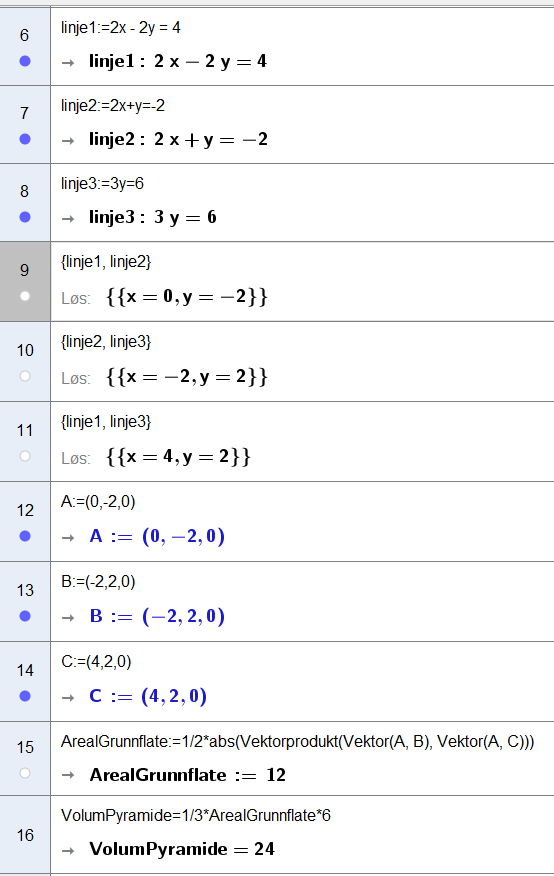
Bruker CAS i Geogebra til å finne volumet av pyramiden. | |||
[[File: R2_H19_del2_2b.png]] | |||
Linje 6,7,8 i CAS: z-verdien er 0 i xy-planet. Definerer de tre linjene som avgrenser grunnflaten til pyramiden. | |||
Linje 9,10,11 i CAS: finner hjørnene til grunnflaten i pyramiden, i xy-planet. | |||
Linje 12,13,14 i CAS: uttrykker hjørnene til grunnflaten som punkter i rommet, punkt A, B og C. | |||
Linje 15 i CAS: Finner arealet av grunnflaten til pyramiden, ved å ta halvparten av absoluttverdien til kryssproduktet til vektor AB og AC (siden kryssproduktet spenner ut et parallellogram, og arealet av en trekant er halvparten av arealet til et parallellogram). | |||
Linje 16 i CAS: Finner volumet av pyramiden med formelen $V=\frac{1}{3}\cdot G\cdot h$. Høyden h er 6, siden z-verdien til punkt P er 6. | |||
Volumet av pyramiden er 24. | |||
==Oppgave 3== | |||
===a)=== | |||
Bruker sum-funksjonen i CAS i Geogebra 6.0. | |||
[[File: R2_H19_del2_3a3.png]] | |||
Vi har vist at Sveins samlede inntekt i årene 2020–2029 da vil bli i overkant av 5,97 millioner kroner. | |||
===b)=== | |||
Bruker sum-funksjonen i CAS i Geogebra 6.0 | |||
[[File: R2_H19_del2_3b2.png]] | |||
Svein må jobbe minst 19,3 år etter at han er ferdig med videreutdanningen, for at den samlede inntekten fra og med 2020 skal bli minst like stor som om han ikke tar videreutdanning. | |||
==Oppgave 4== | |||
===a)=== | |||
Vi har $y'=9,81\cdot(1-\frac{y^2}{k^2}), \quad y(0)=0$ | |||
Siden $y$ er farten, er $y'$ akselerasjonen. Når farten er konstant, er akselerasjonen lik 0. Vi ser av likningen for $y'$ at dersom $k^2$ i nevner er lik $y^2$ i teller (og altså lik $(v_a)^2$ når vi snakker om terminalfarten), så er brøken lik 1, og vi får $(1-1)$ i parentesen, altså 0. Dermed blir akselerasjonen lik 0, og farten er konstant. Vi har $k^2 = (v_a)^2$ når muffinsformen har nådd terminalfarten. | |||
===b)=== | |||
Bruker CAS i Geogebra 6.0. | |||
[[File: R2_H19_del2_4b.png]] | |||
Vi har vist at farten y for denne typen muffinsformer er gitt ved | |||
$y(x)=\frac{9}{5}\cdot(\frac{1-e^{-10,9x}}{1+e^{-10,9x}})$ | |||
Kommentar: uttrykket blir ikke skrevet på samme måte i Geogebra, men under ser vi at uttrykkene er like: | |||
[[File: R2_H19_del2_4b2.png]] | |||
===c)=== | |||
Bruker CAS i Geogebra 6.0. NB: opplevde CAS som meget vrang i denne oppgaven, og måtte prøve mange varianter av samme inntasting før jeg fikk et svar. Får du spørsmålstegn som svar eller andre problemer i CAS på eksamen, ta uansett skjermbilde av det du har forsøkt, det kan være riktig tenkt. | |||
[[File: R2_H19_del2_4c.png]] | |||
Det vil gå 6,79 sekunder fra du slipper en muffinsform av denne typen, til den har falt 12 meter (forkaster negativt svar). | |||
===d)=== | |||
[[File: R2_H19_del2_4d.png]] | |||
Terminalfarten til denne typen muffinsform er 2,66 m/s (forkaster negativt svar). | |||
Siste sideversjon per 6. jul. 2020 kl. 16:57
Diskusjon av denne eksamensoppgaven
Løsningsforslag til del 1 laget av Emilga
Løsningsforslag til del 2 laget av Kristian Saug
Løsningsforslag laget av Ole Henrik Morgenstierne
Løsning til del 1 som videoer laget av Lektor Håkon Raustøl
Løsning til del 2 som videoer laget av Lektor Håkon Raustøl
DEL 1
Oppgave 1
a)
$f(x)=2cos(\pi x)$
$f'(x)=-2 \pi sin(\pi x)$
b)
$g(x)=cos^2 x \cdot sin\, x$
$g'(x)=(cos^2 x)' \cdot sin\, x + cos^2 x \cdot (sin\, x)' \\ = 2cos\, x \cdot (-sin\, x) \cdot sin\, x + cos^2 x \cdot cos\, x \\ = -2sin^2 x \cdot cos x + cos^3 x$
Oppgave 2
a)
$\int_{-1}^{1} (2x^3+3x-1) dx \\ = [ \frac{2}{4}x^4+\frac{3}{2}x^2-x]_{-1}^{1} \\ =(\frac{1}{2}\cdot 1^4+\frac{3}{2}\cdot 1^2-1)-(\frac{1}{2}\cdot (-1)^4+\frac{3}{2}\cdot (-1)^2-(-1)) \\ =(\frac{1}{2}+\frac{3}{2}-1)-(\frac{1}{2}+\frac{3}{2}+1) \\ = -1-1 = -2$
b)
$u=2x^2-1$
$\frac{du}{dx}=4x \Rightarrow dx=\frac{du}{4x}$
$\int \frac{8x}{\sqrt{2x^2-1}} dx = \int \frac{8x}{\sqrt{u}} \cdot \frac{du}{4x} = \int \frac{2}{\sqrt{u}} du = 2 \int u^{-\frac{1}{2}} du \\ = \frac{2}{\frac{1}{2}}\cdot u^{\frac{1}{2}} + C = 4 \cdot \sqrt{u} + C = 4\sqrt{2x^2-1}+C$
c)
$\int \frac{2}{(x+3)(x+1)}dx = \int \frac{A}{(x+3)}+\frac{B}{(x+1)} dx $
Vi bestemmer A og B ved å løse likningen:
$2 = (x+1)A + (x+3)B \\ 2=Ax+A+Bx+3B \\ 2=(A+B)x + A+ 3B$
Telleren har ikke noe x-ledd, så vi har:
I $A+B=0$
II$A+3B=2$
Setter inn $A=-B$ i likning II:
$-B+3B=2 \Rightarrow B=1$
Fra likning I har vi da $A=-1$
Integralet blir da:
$\int \frac{2}{(x+3)(x+1)}dx = \int \frac{A}{(x+3)}+\frac{B}{(x+1)} dx = \int \frac{-1}{(x+3)}+\frac{1}{(x+1)} dx \\ = - \ln|{x+3}| + \ln|{x+1}| + C = \ln|{\frac{x+1}{x+3}}| + C$
Oppgave 3
a)
Summen av en aritmetisk rekke er gitt ved
$S_n=\frac{n\cdot (a_1+a_n)}{2}$
Vi må finne antall ledd i rekken $7+11+....+479+483$.
Ser at $d=4$, så antall ledd (n) blir:
$n=\frac{483-7}{4}+1=\frac{476}{4}+1=119+1=120$
Summen av denne rekken blir:
$S_{120}=\frac{120\cdot (7+483)}{2}= 60\cdot(7+483)=420+28980 =29400$
b)
For en geometrisk rekke har vi
$a_n=a_1\cdot k^{n-1}$
Vi vet at $a_2=6$ og får likning I:
$a_2=a_1\cdot k^{2-1} \\ 6=a_1\cdot k \\ a_1=\frac{6}{k}$
Summen av en geometrisk rekke som konvergerer er gitt ved
$S=\frac{a_1}{(1-k)}$
Vi vet at summen av rekken er 24 og har dermed likning II:
$24=\frac{a_1}{(1-k)} \\ a_1=24(1-k)$
Setter inn $a_1=\frac{6}{k}$ i likning II:
$\frac{6}{k} = 24(1-k) \\ 6=24k(1-k) \\ 6=24k-24k^2 \\ 24k^2-24k+6=0 \\ k^2-k+\frac{1}{4}=0 \\ (k-\frac{1}{2})(k-\frac{1}{2})=0 \\ k=\frac{1}{2} $
Setter inn $k=\frac{1}{2} $ i likning I:
$a_1=\frac{6}{\frac{1}{2}}=12$
Oppgave 4
a)
$2sin(2x)=1$, der $x\in[0,\pi]$
$sin(2x)=\frac{1}{2}$
$ 2x=\frac{\pi}{6} + k \cdot 2 \pi \vee 2x = (\pi - \frac{\pi}{6}) + k\cdot 2\pi \quad \quad k \in \mathbb{Z} $
$ x = \frac{\pi}{12} \vee x = \frac{5\pi}{12} \quad $ kun disse to løsningene gir $x\in[0,\pi]$
$ L = \{ \frac{\pi}{12}, \frac{5\pi}{12} \}$
b)
$2cos^2 x-cos x=1$, der $x\in[0,4\pi]$
$u=cos\,x$
$2u^2-u-1=0 \\ u^2-\frac{1}{2} u - \frac{1}{2}=0 \\ (u+\frac{1}{2})(u-1)=0 \\ u=-\frac{1}{2} \vee u=1 \\ cos\,x=-\frac{1}{2} \vee cos\, x=1$
$cos\,x=-\frac{1}{2} \Rightarrow x=\frac{2\pi}{3} + k\cdot 2\pi \Rightarrow L=\{ \frac{2\pi }{3}, \frac{8\pi}{3} \} $ for $x\in[0,4\pi]$
og $cos\,x=-\frac{1}{2} \Rightarrow x= \frac{4\pi}{3} + k\cdot 2\pi \Rightarrow L=\{ \frac{4\pi}{3}, \frac{10\pi}{3} \}$ for $x\in[0,4\pi]$
$cos\,x=1 \Rightarrow x=0 + k\cdot 2\pi \Rightarrow L=\{0,2\pi,4\pi \}$ for $x\in[0,4\pi]$
$L=\{ 0,\frac{2\pi}{3},\frac{4\pi}{3},2\pi,\frac{8\pi}{3},\frac{10\pi}{3},4\pi \}$
Oppgave 5
B er grafen til f.
Dette fordi $sin^2(x)=0$ for $x=0, x=\pi$ og $x=2\pi$ i intervallet $x\in[0,2\pi]$. Dette er de samme nullpunktene som for $sin(x)$.
I tillegg er $sin^2(x)=1$ for $x=\frac{\pi}{2}$ og $x=\frac{3\pi}{2}$ i intervallet $x\in[0,2\pi]$
Oppgave 6
a)
$f(x)=x+a, \quad 0\leq x \leq 2, \quad a>0$
$\int_{0}^{2} f(x) dx = 3$
$ [ \frac{1}{2} x^2 + ax]_{0}^{2} = 3$
$(\frac{1}{2}\cdot 2^2+a\cdot 2)-(\frac{1}{2}\cdot 0^2+a\cdot 0) = 3$
$\frac{4}{2}+2a-0 = 3$
$2a = 3-2$
$a=\frac{1}{2}$
b)
$V=\int_{0}^{2} \pi (f(x))^2 dx$
$= \pi \int_{0}^{2} (x+a)^2 dx$
$=\pi \int_{0}^{2} (x^2 + 2ax + a^2) dx$
$= \pi [\frac{1}{3}x^3 + \frac{2a}{2} x^2 + a^2x]_{0}^{2}$
$=\pi [(\frac{1}{3}\cdot(2)^3+a\cdot(2)^2 +a^2\cdot 2)-(\frac{1}{3}\cdot(0)^3+a\cdot(0)^2 +a^2\cdot 0)]$
$=\pi(\frac{8}{3}+4a+2a^2)$
Setter inn uttrykket for V i likningen:
$V=\frac{98}{3}\pi$
$\pi(\frac{8}{3}+4a+2a^2) = \frac{98}{3}\pi \quad | : \pi$
$\frac{8}{3}+\frac{3\cdot4a}{3}+\frac{3\cdot 2a^2}{3}=\frac{98}{3}$
$\frac{8}{3}+\frac{12a}{3}+\frac{6a^2}{3}=\frac{98}{3} \quad |\cdot 3$
$6a^2+12a+8-98=0$
$6a^2+12a-90=0 \quad |:6$
$a^2+2a-15=0$
$(a+5)(a-3)=0$
$a=-5 \vee a=3$
Forkaster $a=-5$ siden vi må ha $a>0$. Vi har da $a=3$.
Oppgave 7
a)
I xz-planet er $y=0$. Setter inn $y=0$ i uttrykket for $y$:
$y=2-t \\ 0=2-t \\ t=2$
Setter inn $t=2$ i uttrykket for $x$:
$x=1+2t \\ x=1+2\cdot 2 \\ x=5$
Setter inn $t=2$ i uttrykket for $z$:
$z= 6+t \\ z=6+2 \\ z=8$
Skjæringspunktet mellom linjen $\ell$ og xz-planet er (5,0,8).
b)
Linjen $\ell$ står vinkelrett på planet $\alpha$, og retningsvektoren til linjen $\ell$ er derfor lik normalvektoren $\vec{n_\alpha}$ til planet $\alpha$. Dermed er skalarproduktet av $\vec{n_\alpha}$ og en vektor i planet, lik 0.
Likningen for planet er derfor gitt ved:
$[a,b,c] \cdot [x-x_0, y-y_0, z-z_0]=0$
$a(x-x_0)+b(y-y_0)+c(z-z_0)=0$
Der a,b og c er koordinatene til planets normalvektor, og $x_0,y_0,z_0$ er et punkt i planet. Vi har $\vec{n_\alpha}=[2,-1,1]$ og punktet $P(2,-2,6)$.
$2(x-2)-1\cdot(y-(-2))+1\cdot(z-6)=0 \\ 2x-4-(y+2)+z-6=0 \\ 2x-y+z-4-2-6=0 \\ 2x-y+z-12=0$
Likningen for planet $\alpha$ er $2x-y+z-12=0$.
c)
Setter inn uttrykkene for x,y og z fra parameterfremstillingen til linjen $\ell$, i likningen for planet $\alpha$:
$2x-y+z-12=0 \\ 2\cdot ( 1+2t ) - (2-t ) + (6+t) - 12 = 0 \\ 2+4t-2+t+6+t-12=0 \\ 6t-6 = 0 \\ t=1$
Setter inn $t=1$ i uttrykkene for x,y og z fra parameterfremstillingen til linjen $\ell$:
$x= 1+2t = 1+2\cdot 1=3$
$y = 2-t = 2-1=1$
$z= 6+t=6+1=7$
Skjæringspunktet mellom $\alpha$ og $\ell$ er (3,1,7).
Oppgave 8
Vi har gitt differensiallikningen:
$y' -2y=x, \quad y(0)=1$
a)
Integrerende faktor er $e^{-2x}$
$y' -2y=x$
$e^{-2x} y' - 2 e^{-2x} y = x e^{-2x} $
$(e^{-2x}y)'= x e^{-2x}$
$y e^{-2x} = \int x e^{-2x} dx$
Bruker delvis integrasjon, der $u=x$, $u'=1$, $v'= e^{-2x}$, $v=-\frac{1}{2}e^{-2x}$
$y e^{-2x} = x\cdot (-\frac{1}{2}e^{-2x})-\int (-\frac{1}{2}e^{-2x})dx$
$y e^{-2x} = -\frac{1}{2} x e^{-2x}- (-\frac{1}{2})\cdot(-\frac{1}{2})\cdot e^{-2x}+C$
$y (x) = -\frac{1}{2} x-\frac{1}{4} + C e^{2x}$
Vi har $y(0)=1$
$-\frac{1}{2} \cdot 0-\frac{1}{4} + C e^{2\cdot 0} = 1$
$0-\frac{1}{4}+C \cdot 1 = 1$
$C=1+\frac{1}{4}$
$C=\frac{5}{4}$
Setter inn verdien for C i likningen for y:
$y(x)=-\frac{1}{2}x-\frac{1}{4}+\frac{5}{4} e^{2x}$
b)
Finner stigningstallet til tangenten til y i punktet (0,1):
$y'=x+2y \\ y' = 0+2\cdot 1 \\ y'= 2$
Finner likningen for tangenten til y i punktet (0,1):
$(y-y_1)=a(x-x_1) \\ (y-1)=2(x-0) \\ y=2x+1$
Oppgave 9
Finner lengden av vektorene mellom sentrum av sirklene:
$\vec{AB}=[1-1,2-(-1), 4-0] = [0,3,4]$
$|\vec{AB}| = \sqrt{0^2+3^2+4^2} = \sqrt{25} = 5$
$\vec{BC}=[5-1, 1-2, -4-4] = [4,-1,-8]$
$|\vec{BC}|=\sqrt{4^2+(-1)^2+(-8)^2} = \sqrt{81} = 9$
$\vec{AC}=[5-1, 1-(-1), -4-0]=[4, 2, -4]$
$|\vec{AC}|=\sqrt{4^2+2^2+(-4)^2}=\sqrt{36}=6$
Finner radien $a, b$ og $c$ til hver av kulene:
$I \quad \quad a+b=5 \\ II \quad \, \, \, b+c=9 \\ III \quad a+c=6$
$I \quad \quad a = 5-b \\ II \quad \, \, \, c=9-b \\ III \quad 5-b+9-b=6 \\ \quad \quad -2b = 6-5-9 \\ \quad \quad \, \, \, b=\frac{-8}{-2}=4 $
$I \quad \quad a = 5-4=1 \\ II \quad \, \, \, c=9-4 = 5$
Radien til kulen med sentrum i A er 1, radien til kulen med sentrum i B er 4, radien til kulen med sentrum i C er 5.
Oppgave 10
Vi skal vise at $n^3-n$ er delelig med 3 for alle $n \in \N$
1. Induksjonsgrunnlag: $n=1$ gir $1^3-1 = 0$, som er delelig med 3.
2. Induksjonstrinnet: Vi antar at $n^3-n$ er delelig delelig med 3 når $n=k$. Med $n = k+1$ får vi:
$(k+1)^3-(k+1) \\= (k+1)((k+1)^2-1) \\= (k+1)((k^2+2k+1)-1) \\= (k+1)(k^2+2k) \\=k^3+2k^2+k^2+2k \\=k^3+3k^2+2k \\=k^3+3k^2+2k+k-k\\=k^3-k+3k^2+3k \\= (k^3-k) + 3(k^2+k)$
$k^3-k$ er delelig med 3, ifølge antakelsen for $n=k$. $3(k^2+k)$ er en faktor av 3, og er derfor delelig med 3. Summen av to ledd som begge er delelig med 3, er også delelig med 3. Vi har vist at $n^3-n$ er delelig med 3 for $n=k+1$.
$n^3-n$ er delelig med 3 for alle $n \in \N$, hvilket skulle vises.
DEL 2
Oppgave 1
a)
Bruker Geogebra til å tegne grafene til f og g i samme koordinatsystem.
b)
Bruker CAS i Geogebra til å bestemme arealet under grafen til f og arealet under grafen til g.
Arealet under grafen til f er 157,91 og arealet under grafen til g er også 157,91.
c)
Bruker CAS i Geogebra til å finne volumet til hvert av de to omdreiingslegemene.
Volumet til omdreiingslegemet til f er 8174,07.
Volumet til omdreiingslegemet til g er 7996,42.
d)
Bruker CAS i Geogebra til å vise at arealet til F er uavhengig av k.
Vi ser i linje 6 at arealet ikke er avhengig av k, hvilket skulle vises. $16\pi^2$ er for øvrig samme verdi som vi fikk i a).
e)
Bruker CAS til å bestemme hvilken verdi for k som gir minst volum til omdreiingslegemet.
$k=4$ gir minst volum.
Oppgave 2
a)
Bruker CAS i Geogebra til å finne skjæringspunktet til de tre planene.
Planene skjærer hverandre i punktet P(3,-2,6).
b)
Bruker CAS i Geogebra til å finne volumet av pyramiden.
Linje 6,7,8 i CAS: z-verdien er 0 i xy-planet. Definerer de tre linjene som avgrenser grunnflaten til pyramiden.
Linje 9,10,11 i CAS: finner hjørnene til grunnflaten i pyramiden, i xy-planet.
Linje 12,13,14 i CAS: uttrykker hjørnene til grunnflaten som punkter i rommet, punkt A, B og C.
Linje 15 i CAS: Finner arealet av grunnflaten til pyramiden, ved å ta halvparten av absoluttverdien til kryssproduktet til vektor AB og AC (siden kryssproduktet spenner ut et parallellogram, og arealet av en trekant er halvparten av arealet til et parallellogram).
Linje 16 i CAS: Finner volumet av pyramiden med formelen $V=\frac{1}{3}\cdot G\cdot h$. Høyden h er 6, siden z-verdien til punkt P er 6.
Volumet av pyramiden er 24.
Oppgave 3
a)
Bruker sum-funksjonen i CAS i Geogebra 6.0.
Vi har vist at Sveins samlede inntekt i årene 2020–2029 da vil bli i overkant av 5,97 millioner kroner.
b)
Bruker sum-funksjonen i CAS i Geogebra 6.0
Svein må jobbe minst 19,3 år etter at han er ferdig med videreutdanningen, for at den samlede inntekten fra og med 2020 skal bli minst like stor som om han ikke tar videreutdanning.
Oppgave 4
a)
Vi har $y'=9,81\cdot(1-\frac{y^2}{k^2}), \quad y(0)=0$
Siden $y$ er farten, er $y'$ akselerasjonen. Når farten er konstant, er akselerasjonen lik 0. Vi ser av likningen for $y'$ at dersom $k^2$ i nevner er lik $y^2$ i teller (og altså lik $(v_a)^2$ når vi snakker om terminalfarten), så er brøken lik 1, og vi får $(1-1)$ i parentesen, altså 0. Dermed blir akselerasjonen lik 0, og farten er konstant. Vi har $k^2 = (v_a)^2$ når muffinsformen har nådd terminalfarten.
b)
Bruker CAS i Geogebra 6.0.
Vi har vist at farten y for denne typen muffinsformer er gitt ved
$y(x)=\frac{9}{5}\cdot(\frac{1-e^{-10,9x}}{1+e^{-10,9x}})$
Kommentar: uttrykket blir ikke skrevet på samme måte i Geogebra, men under ser vi at uttrykkene er like:
c)
Bruker CAS i Geogebra 6.0. NB: opplevde CAS som meget vrang i denne oppgaven, og måtte prøve mange varianter av samme inntasting før jeg fikk et svar. Får du spørsmålstegn som svar eller andre problemer i CAS på eksamen, ta uansett skjermbilde av det du har forsøkt, det kan være riktig tenkt.
Det vil gå 6,79 sekunder fra du slipper en muffinsform av denne typen, til den har falt 12 meter (forkaster negativt svar).
d)
Terminalfarten til denne typen muffinsform er 2,66 m/s (forkaster negativt svar).