1T 2013 vår LØSNING
Del I
Oppgave 1
$ \displaystyle \frac{ 750 000 }{0.005} = \frac{ 7.5 \cdot 10^5 }{ 0.5 \cdot 10^{-2} } = 15 \cdot 10^{5 - (-2)} = 1.5 \cdot 10^8 $
Oppgave 2
$ \displaystyle \begin{align*} (1)\quad 2x + 3y & = 7 \\ (2)\quad 5x - 2y & = 8 \end{align*} $
Dersom vi ser på $2 \cdot (1) + 3 \cdot (2)$ ser vi at vi får likningen
$ \begin{align*} (4x + 6y) + (15x - 6y) & = 14 + 24 \\ 19x & = 19 + 19 \\ x & = 2 \end{align*} $
Alternativt kan innsetningsmetoden brukes, men da må en hanskes med brøker. Uansett setter vi inn $x$ verdien eksempelvis i $(1)$ finner vi at
$3y = 7 - 2x = 3$, så $y=1$ og $x=2$.
Oppgave 3
$ \displaystyle \frac{ x^2 - 16 }{ x^2 - 8x + 16 } = \frac{ (x - 4)(x + 4) }{ (x-4)^2 } = \frac{ x + 4}{ x - 4 } $ .
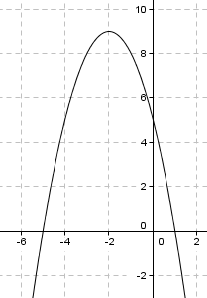
Oppgave 4
Likningen for en rett linje er $y = ax + b$, her er stigningstallet gitt som
$ \displaystyle a = \frac{ 3 - 0 }{0 - 6} = - \frac{ 1 }{ 2 } $
slik at vi kan skrive
$ \displaystyle y = - \frac{1}{2}x + b $
for å bestemme $b$ bruker vi punktet (0,3)
$ \displaystyle y= - \frac 12x +b \\ 3 = -\frac 12 \cdot 0 +b \\ b=3 \\ y= - \frac 12x + 3 $
Dette kunne vi sett direkte fra figuren siden linjen skjærer y-aksen i 3, dvs. b = 3.
$ \displaystyle y =- \frac{1}{2}x + 3\:. $
Oppgave 5
Skriver om alle uttrykkene
$ (1/2)^0 = 1 \\ \sqrt[3]{27} = \sqrt[3]{3^3}=3 \\ \sqrt{20} = \sqrt{4 \cdot 5} = \sqrt{5} > 2 \sqrt{4} = 4
\\ 1/9 - 3^{-2} = 0 \\ 0 \leq \sin 50^\circ \leq 1 \\ \lg 150 = lg(100 \cdot 1,5) \lg 100 + \lg 1,5 = 2 + \log 1,5 $.
Herfra så får vi i stigende rekkefølge
$ \displaystyle \frac{1}{9} - 3^{-2} < \sin 50^\circ < (1/2)^0 < \lg(150) < 27^{1/3} < \sqrt{20}. $
Oppgave 6
Enten er begge kulene blå, eller så er begge kulene røde, summen er hva vi er ute etter.
$ \displaystyle (1) = P(\text{blå} \cap \text{blå}) = \frac{2}{5} \cdot \frac{1}{4} = \frac{1}{10} $
og
$ \displaystyle (2) = P(\text{rød} \cap \text{rød}) = \frac{3}{5} \cdot \frac{2}{4} = \frac{3}{10} $
Summen er da
$\displaystyle P(2 \cup 2) = \frac{4}{10} = \frac{2}{5} \approx 40 \percent $.
Oppgave 7
a) Legg merke til at
$ \begin{align*} f(x) = & -x^2 - 4x + 5 \\ = & -(x^2 -x + 5x - 5 ) \\ = & - [x(x-1) + 5(x-1)] \\ & = (x+5)(1-x) \end{align*} $
Nullpunktene er dermed $x=-5$ eller $x=1$. Alternativt kan man bruke andregradsformelen.
b)
$f'(x) = -2x-4 \\ f'(x) =0 \\ x=-2 \\ f(-2) = 9 $
Punktet (-2,9) er et toppunkt på grafen fordi andregradsleddet har en negativ koeffisient, dvs. grafen vender sin hule side ned.
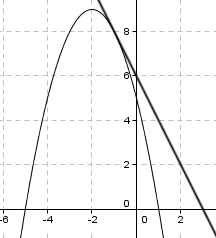
c)
d)
En linje er på formen $y = Ax+b$, hvor vi har at $ a = f'(1) = -2(-1) - 4 = -2$
$f(-1) = 8$ Tangeringspunktet er (-1,8)
$ y = -2x+b \\ 8= -2 \cdot -1 +b \\ b=6 $
Hvilket gir likningen $ y=-2x+6$
Oppgave 8
a) Fra pytagoras har vi at siden trekanten $AOC$ er rett så er
$ AC^2 = AO^2 + OC^2 = r^2 + r^2 = 2 r^2 $
Siden lengden er positiv må $AC = \sqrt{2} \cdot r$, som ønsket.
b)
Arealet av $\triangle AOC$ er gitt som
$ \displaystyle A_1 = \frac{1}{2} r \cdot r = \frac{1}{2} r^2. $
Arealet av sirkelbuen med grunnlinje $AB$ er gitt som
$ \displaystyle A_S = \pi \cdot r^2 / 2 $.
Arealet av halvsirkelen med grunnlinje $AC$ er gitt som
$ \displaystyle A_C = \pi \cdot (AC/2)^2/2 = \pi \cdot r^2 / 4 = A_S / 2 $
Området mellom det blå, og trekanten er gitt som
$ \displaystyle A_M = A_S / 2 - A_1 $
Slik at for å finne arealet av det blå, kan vi regne ut arealet av halvsirkelen, og trekke fra det skaverte området. Da fås
$ \displaystyle A_B = AC - A_M = A_S/2 - ( A_S/2 - A_1) = A_1 $
som ønsket.
Del II
Oppgave 1
Her har vi en $30-60-90$ trekant. Da er hypotenusen dobbelt så lang som den korteste kateten. Dette kan vi skrive som
$ \displaystyle 4^2 + x^2 = (2x)^2 \\ 16 + x^2 = 4x^2 \\ 16 = 3x^2 \\ x^2 = \frac{16}{3} \\ x= \frac{4}{\sqrt 3} $
Slik at den korteste kateten er $\frac{4}{\sqrt{3}} \approx 2.31$ og hypotenusen er $\frac{8}{\sqrt{3}} \approx 4.62$
Oppgave 2
a)
Her vil sinus-setningen være nyttig. Den sier at om $ABC$ er en trekant $\Delta ABC$, med interne vinkler $A, B, C$ og sider $a, b, c$ så er
$ \displaystyle \frac{ a }{ \sin A } = \frac{ b }{ \sin B } = \frac{ c }{ \sin C } $
bruker vi dette så har vi dette at
$ \displaystyle \begin{align*} \frac{ BD }{ \sin 60^\circ } & = \frac{ 5 }{ \sin 38.2^\circ } \\ BD & = \frac{ 5 }{ 2 } \sqrt{3} \cdot \sin 38.2^\circ \\ BD & \approx 7.0 \end{align*} $
b)
Her kan vi eksempelvis bruke at arealet
av en trekant er gitt som $A = a \cdot b \cdot \sin (A) / 2 $.
Dersom vi ser først på trekant ABD først, har en at
$ \displaystyle \triangle ABD \approx \frac{1}{2} \cdot 5 \cdot 7 \cdot \sin( 180-60-38.2) \approx 17.32 $
For å finne arealet av den siste trekanten, kan eksempelvis herons formel benyttes. Her har en at $S \approx (4 + 6 + 7)/2 = 17/2$ hvor $S$ er halvparten av omkretsen til trekant $BCD$. Da er arealet
$ \triangle BCD = \sqrt{ S(S-a)(S-b)(S-c) } = \sqrt{ \frac{17}{2}\left( \frac{17}{2} - 4 \right) \left( \frac{17}{2} - 6 \right)\left( \frac{17}{2} - 7 \right) } = \frac{3}{4}\sqrt{255} \approx 11.977 $
Eller så kan vi bruke cosinussetningen til å først finne vinkel C.
$ \displaystyle \begin{align*} C & = \arccos \left( \frac{ a^2 + b^2 - c^2 }{ 2ab } \right) \\ & \approx \arccos \left( \frac{ 4^2 + 6^2 - 7^2 }{ 2 \cdot 4 \cdot 6 } \right) \\ & = \arccos \left( \frac{1}{16} \right) \\ & \approx 86.420 \end{align*} $
Også bruke sinussetningen slik at arealet kan skrives som
$ \triangle BCD \approx \frac{1}{2} \cdot 4 \cdot 6 \cdot \sin(86.420) \approx 11.97 $
samme som før.
Slik at det totalet arealet kan skrives som
$ \square ABCD = \Delta ABD + \Delta BCD \approx 29.297 $
Så arealet av figuren er omtrentlig $29$.
Oppgave 3
a)
Antall fargeblinde kan skrives som
$ \displaystyle \frac{8}{100} \cdot 4000 + \frac{1}{100} \cdot 6000 = 380 $
Slik at sannsynligheten for at en person er fargeblind (FB) er gitt som
$ \displaystyle \begin{align*} P(FB) & = \frac{ \text{ gunstige } }{ \text{ mulige } } & = \frac{ 380 }{ 4000 + 6000 } & = \frac{ 19 }{ 500 } & \approx 3.8 \: \percent \end{align*} $
Altså er sannsynligheten for at en tilfeldig person er fargeblind er $3.8 \percent$.
b)
Antall kvinner som er fargeblinde er
$ \displaystyle \frac{1}{100} \cdot 6000 = 60 \:, $
slik at sannsynligheten for at en kvinne er fargeblind er gitt som
$ \displaystyle \begin{align*} P(FB \cap \text{Kvinne} ) & = \frac{ 60 }{ 380 } \\ & = \frac{ 3 }{ 19 } \\ & \approx 15.789 \: \percent \end{align*} $
Oppgave 4
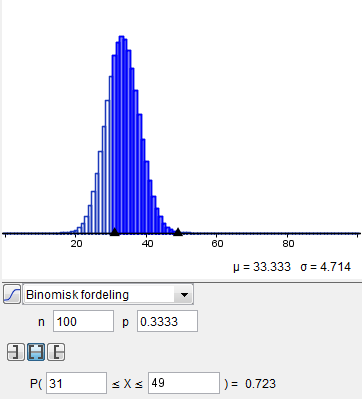
a) Her bruker vi binomisk fordeling og får da
Definerer først sannsynligheten for at $X = k$, ønsker å flytte fra byen som
$ \displaystyle P(X = k) = \binom{100}{k} \left( \frac{1}{3} \right)^k \left( \frac{2}{3} \right)^{100 - k} $
Slik at sannsynligheten for at nøyaktig $30$ ønsker å flytte fra byen er gitt som
$ P(X = 30 ) \approx 0.067284 =6.7284 \: \percent $
Slik at sannsynligheten for at nøyaktig $30$ personer, ønsker å flytte fra byen er ca $6.7$ prosent.
b)
Her legger man sammen alle sannsynlighetene mellom $30$ og $50$, geogebra eller en kraftig kalkulator klarer dette fint.
$ P(31 < X < 49) = \sum_{k=30}^{50} P(k) \approx 0.72303 $
Altså var sannsynligheten for at mellom $30$ og $50$ flyttet ut ca $72.3$ prosent.
Oppgave 5
a) La $M$ st for menn og $P$ for kvinner da har vi likningene
$ \begin{array}{rcrcr} M & + & K & = & 1000 \\ \frac{21}{100} M & + & \frac{16}{100} K & = & 1000/5 \end{array} $
Her deler vi på $5$, siden det bare var $1$ av $5$ som trente.
b) Begyner med løse øverste likning for $K$, da fås $K = 1000 - M$. Deretter ganges nederste likning med $100$, også settes inn opplysningen om $K$. Da fås
$ \begin{align*} \frac{21}{100} M + \frac{16}{100} K & = 200 \\ 21 M + 16 K & = 20 000 \\ 21 M + 16(1000 - M) & = 20 000 \\ 5 M + 16 000 & = 20 000 \\ M & = 800 \end{align*} $
Og tilsvarene så er $K = 1000 - 800 = 200$. Altså var det totalt sett $800$ menn og $200$ kvinner som deltok på undersøkelsen.
Oppgave 6
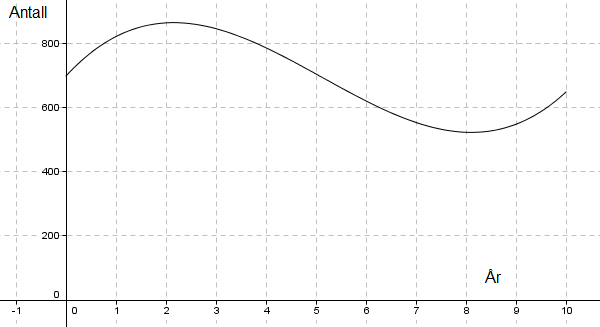
a)
b)
$ h(t) = 3.25 t^3 - 50 t^2 + 170 t + 700 $, derivasjon gir
$ h'(t) = 9.75 t^2 - 100 t + 170 $
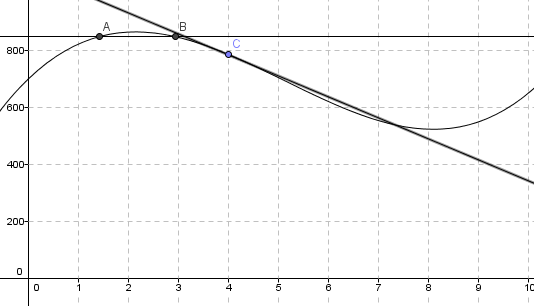
Setter den deriverte lik null og finner at hjortebestanden var størst etter 2,14 år, altså tidlig på vinteren i 1992. Er det særlig realistisk at en slik bestand har en topp på vinteren??
Avlest grafen kan man si at det var ca. 870 dyr i området. Siden dette er en modell er den uansett ikke helt nøyaktig.
c)
Ser fra figuren at
$h(t)>850$ når $1.4224 < t < 2.94526$
Denne ulikheten beskriver når det var flere enn $850$ hjort i området.
d)
$ h'(4) = -74 $
Det dette forteller oss er at i begynnelsen av 1994 var vekstraten negativ, bestanden lå an til å minke med 74 dyr per år.
Oppgave 7
a) Her vil hypotenusen beskrive radius i sirkelen slik at pytagoras gir oss
$ r = \sqrt{5^2 + 2,5^2} \approx 5,6 $
b)
Diagonalen i rektangelet er 20, og langsiden 2x. Kortsiden blir da
$\sqrt{20^2 - 4x^2}$
Arealet finner man ved å multiplisere langside med kortside:
$A(x)=2x \cdot \sqrt{400 - 4x^2} = 2x \cdot 2 \sqrt{100 -x^2} = 4x \sqrt{100-x^2}$
c)
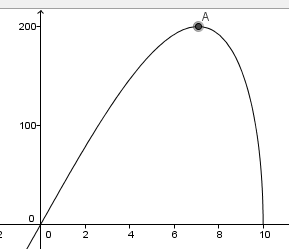
Vi tegner grafen til A(x) i Geogebra og bruker ekstremalpunktsfunksjonen. Vi ser at funksjonen har et maksimum for x = 7,07. Da er arealet 200.
Lengden av rektangelet med størst areal er $2 \cdot x = 2 \cdot 7,07 = 14,1 $
Vi vet fra b) at bredden er $ \sqrt{20^2 - 4 \cdot 7,07^2} = 14,1$
Ettersom bredde og lengde er lik har vi et kvadrat.
Oppgave 8
$ \displaystyle \frac{c}{d} - \frac{c+7d}{d+7d} = \\ \frac{c}{d} - \frac{c+7d}{8d} =\\ \frac{8c}{8d} - \frac{c+7d}{8d} =\\ \frac{7c-7d}{8d} = \\ \frac 78 \left( \frac cd - 1 \right) $
Dette skal være lik åtte.
$ \frac 78 \left( \frac cd - 1 \right) = 8 \\ \frac cd - 1 = \frac {64}{7} \\ \frac cd = \frac {64}{7} + 1 \\ \frac cd = \frac {71}{7} $