Proposjonalitet
Forhold
Forholdet mellom a og b er a : b, eller, <math> \frac ab</math>. Dersom det er 10 gutter og 5 jenter i en klasse er forhldet mellom gutter og jenter <math> \frac {10}{5} = \frac {2}{1}</math>, man sier at forholdet mellom gutter og jenter er "to til en". Forholdet mellom jenter og gutter er "en til to".
Eksempel 1:
Enkelte båtmotorer krever olje i bensinen. En spesiell motor krever blandingsforholdet 1:25. Det betyr at dersom du har en liter olje, må du blande inn 25 liter bensin for at blandingsforholdet blir riktig. Dersom du har 10 liter bensin må du blande inn <math> 10 liter \cdot \frac{1}{25}= 10 \cdot 0,04 liter = 0,4 liter olje</math> 4 dl. olje for at forholdet skal bli riktig.
Eksempel 2:
Tilsvarende, dersom du har 7 desiliter olje må du blande inn 0,7 liter .25 = 17,5 liter bensin.</math>
Blandinger
Dersom vi blander etter forholdet <math>\frac ab </math> består blandingen av a + b deler. Stoff a vil utgjøre <math>\frac a{a+b} </math> av hele blandingen.
Eksempel 3:
En del saft blandes med 12 deler vann. Forholdet er 1 : 12 eller .Legg merke til at blandingen nå totalt består av 13 deler, 1 del saft + 12 deler vann, slik at mengden av ren saft i blandingen er <math>\frac 1{13} </math> og mengden av rent vann i blandingen er <math>\frac {12}{13} </math>
Proporsjoner
En proporsjon sier at to forhold er like store. a forholder seg til b som c forholder seg til d.
<math>\frac ab = \frac cd </math>
Vi kryssmultipliserer og får ad = bc.
Eksempel 4:
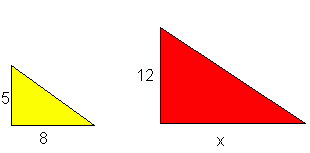
Vi har to formlike trekanter. I den ene trekanten kjenner vi lengden av begge katetene, men i den andre kjenner vi bare et.
Vi finner det ukjente på følgende måte:<math> \frac 58 = \frac {12}{x} \Rightarrow 5x = 96 \Rightarrow x= \frac {96}5 \Rightarrow x =19,2</math>
Eksempel 5:
Erik liker saft og vann blandet i forholdet 1:6. Hvor mye saft må tilsettes 2,4 liter vann for å få dette forholdet?<math> \frac{1}{6}= \frac {x}{2,4} \Rightarrow 6x=2,4 \Rightarrow x=0,4</math>
SVAR: 0,4 liter saft.
Proporsjonalitet
y og x er proporsjonale når y = kx . k er konstant og kalles proporsjonalitetsfaktoren. Vi observerer at dette er ligningen for den rette linje uten konstantleddet b. Vi har at
Eksempel 6:
Hvor mye du må betale når du kjøper appelsiner avhenger av hvor mange kilo du kjøper og kiloprisen. Kiloprisen er konstant. Totalpris (y) = kilopris(k) ·antall kilo (x). Dersom kiloprisen er 4 kr,- får vi følgende sammenheng:y = 4x
En rettlinjet graf som går gjennom origo representerer forholdet mellom to proporsjonale størrelser. En rettlinjet graf som IKKE går gjennom origo representerer IKKE to proporsjonale størrelser.
Eksempel 7:
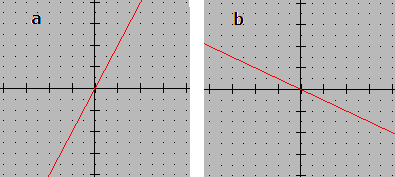
Hvilke av grafene representerer sammenhenger mellom to proporsjonale størrelser?
a:<math>y = 2x</math>
b:<math>y = - \frac 12x</math>
Man observerer at grafene som går gjrnnom origo ikke har konstantledd. Disse viser en proporsjonal sammenheng.
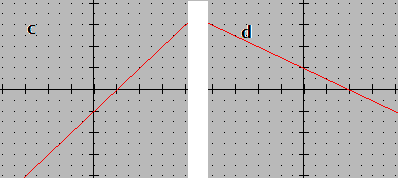
c:<math>y = x - 1</math>
d:<math>y = - \frac 12x + 1</math>
Dersom man har en tabell med sammenhørende x og y verdier og ønsker å undersøke om x og y er proporsjonale, gjør man det ved å dividere y verdi med sammenhørende x verdi. Dersom man får samme svar for alle tallpar (x,y verdier) er x og y proporsjonale. Den verdien man har funnet er proporsjonalitetskonstanten k.
Omvendt Proporsjonalitet
y og x er omvendt proporsjonale når . k er konstant. Vi har k = xy.
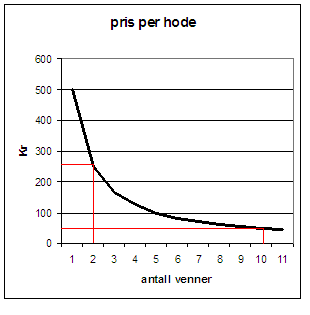
Eksempel 6: Du leier en ungdomsklubb for en kveld for kr. 500,- Du inviterer dine venner til fest. Hvor mye hver enkelt må betale (y) kommer an på hvor mange som takker ja til invitasjonen (x). Vi sier at prisen hver enkelt må betale er omvendt proporsjonal med antall gjester. Vi får
Legg merke til at grafen avtar sterkest i begynnelsen, for så å flate ut når antall gjester øker.