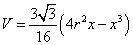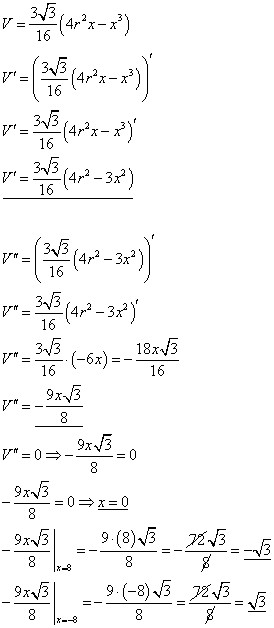Derivasjon - optimalisering

[Razzy]

I en kule med radius r er innskrevet et regulært trekantet prisme. Prismets høyde er x.

Prismets volum er gitt ved formelen



Finn den største verdien som prismevolumet kan ha, når x varierer og r er konstant. Hvor mange prosent av kulevolumet utgjør prismevolumet i dette tilfelle?



Kommentar: Jeg prøvd dette i en god stund uten hell:

Jeg ønsker ved bruk av optimalisering å bestemme den størst mulig volum. Ergo jeg er nødt til å derivere volumet gitt ved formelen ovenfor for å finne ut maksverdien dette volumet kan ha. Men før jeg gjør dette må jeg omskrive r ved bruk av trigonometri, for kun ha x-ser i mitt formelen jeg skal derivere.

Jeg vil ikke ha fasit, men gjerne en kommentar om jeg tenker riktig? Foreløbig har jeg laget flere problemer enn løsninger - og det er jo forsåvidt greit, bare de problemen er lettere enn det man startet med. men nææh.

[Vektormannen]

Det gjør ikke noe at det står r i uttrykket, for r holdes konstant. Den vil altså ikke virke inn på volumforandringen når x forandrer seg. Du kan altså derivere uttrykket slik det står, og behandle r som du behandler andre konstanter.

[Razzy]

Det gjør ikke noe at det står r i uttrykket, for r holdes konstant. Den vil altså ikke virke inn på volumforandringen når x forandrer seg. Du kan altså derivere uttrykket slik det står, og behandle r som du behandler andre konstanter.

Kjempeflott, da tror jeg at jeg kom i mål. Jeg satt det deriverte av uttrykket lik null og sjekket om det var et toppunkt jeg fikk ved å bruke fortegnslinjer.

Takk igjen lektor Vektormannen

[Razzy]

Det gjør ikke noe at det står r i uttrykket, for r holdes konstant. Den vil altså ikke virke inn på volumforandringen når x forandrer seg. Du kan altså derivere uttrykket slik det står, og behandle r som du behandler andre konstanter.

Kjempeflott, da tror jeg at jeg kom i mål. Jeg satt det deriverte av uttrykket lik null og sjekket om det var et toppunkt jeg fikk ved å bruke fortegnslinjer.

Takk igjen lektor Vektormannen

Var visst litt vel kjapp på avtrekkeren her...


i
1. Jeg finner den deriverte, helt ok.
2. Jeg setter x=0 for å finne ut maksimum, men hvordan får jeg vist at dette er maksimum? Burde vel bytte ut r med noe her?

[Nebuchadnezzar]

2. Sett på fortegnslinje for f'(x)

Elelr ta dobbelderiverttesten

[Razzy]

2. Sett på fortegnslinje for f'(x)

Elelr ta dobbelderiverttesten

"For å kunne sette noe på fortegnslinje må faktorene være i førstegrad"

[tex]4 a^2-3 x^2[/tex] - Kan denne faktoriseres?

Ifølge Wolfram (http://www.wolframalpha.com/input/?i=%2 ... -3x%5E2%29):

Den gir med disse nullpunktene: [tex]x = -{{2 r}\over {sqrt3}}[/tex] og [tex]{{2 r}\over {sqrt3}}[/tex]

Dermed: [tex]4 r^2-3 x^2[/tex] = [tex]$$\left( {x - {{2r} \over {\sqrt 3 }}} \right)\left( {x + {{2r} \over {\sqrt 3 }}} \right)$$[/tex]

Det jeg skal studere i en fortegnslinje er da:

[tex]$${{3\sqrt 3 } \over {16}}\left( {x - {{2r} \over {\sqrt 3 }}} \right)\left( {x + {{2r} \over {\sqrt 3 }}} \right)$$[/tex]

[Razzy]

Først og fremst:

[tex]$$4{r^2} - 3{x^2} \ne \left( {x - {{2r} \over {\sqrt 3 }}} \right)\left( {x + {{2r} \over {\sqrt 3 }}} \right)$$[/tex]

Forsøker meg på noe annet: Hva hvis det deriverte uttykket går mot uendelig? Altså:



Her vil vi jo få et svar, og det varet vil fortelle oss hvilken verdi x vil nærme seg når x går mot uendelig. Dette svaret putter vi så inn i volumformelen og jeg er fornøyd.

Går dette? Nå er jo problemet bare å løse dette limit uttrykket.

Edit: Tidligere slet jeg jo som sagt med å faktorisere den deriverte.

[Vektormannen]

Hvorfor vil du finne grensen når x går mot uendelig egentlig?

Når det gjelder faktoriseringen så er det ikke noe annet enn konjugatsetningen: [tex]4r^2 - 3x^2 = (2r-\sqrt 3 x)(2r + \sqrt 3 x)[/tex].

[Razzy]

Hvorfor vil du finne grensen når x går mot uendelig egentlig?

Når det gjelder faktoriseringen så er det ikke noe annet enn konjugatsetningen: [tex]4r^2 - 3x^2 = (2r-\sqrt 3 x)(2r + \sqrt 3 x)[/tex].

Det var vel et cowboy-move tenker jeg - dvs dårlig forslag.

Takk! Til faktoriseringen, nå går det sikkert. (trodde jeg hadde kontroll på tredjekvadratsetning)

[mstud]

1. Jeg finner den deriverte, helt ok.
2. Jeg setter x=0 for å finne ut maksimum, men hvordan får jeg vist at dette er maksimum? Burde vel bytte ut r med noe her?

Du har fått god hjelp her av andre, men ville bare gjøre oppmerksom på hvorfor dette forslaget ditt var feil ... :

Hvorfor setter du egentlig x=0 for å finne maksimum her?

Da måtte du først vite at x=0, gjør den deriverte av det opprinnelige uttrykket lik 0, og det gjør det ikke...

[tex]\frac {3\sqrt {3}}{16} (4r^2-3x^2)=0[/tex] gir ikke akkurat x=0...

I toppunktet til en funksjon, er det jo den deriverte av uttrykket som er 0, og ikke x som er lik 0. (Så sant ikke toppunktet er i x=0, men det kan man i så fall ikke bare anta).

Du får: (4r^2-3x^2)=0 (siden vi vet at [tex]\frac {3\sqrt {3}}{16} \neq 0[/tex] )

Når du da faktoriserer slik Vektormannen skrev er du nokså nær mål...

Du har da[tex]4r^2-3x^2=(2r-\sqrt {3} x)(2r+\sqrt {3} x) = 0[/tex]

og det gjenstår bare å finne ut hvilken verdi av som er toppunkt, gjerne vha et av forslagene til Nebuchadnezzar

Jeg tror jeg ville foretrekke det 2. forslaget hans, nemlig å derivere en gang til og bruke når den dobbeltderiverte er positiv / negativ,men det er nå bare meg.

Hvis du husker om grafen "smiler" (dobbeltderivert positiv) eller er "sur" (dobbeltderivert negativ) i et toppunkt... Var vel noe slikt man lærte første gang, og kan brukes litt mer humoristisk enn at grafen krummer oppover / nedover..

Men jeg vet det finnes de som liker bedre å tegne fortegnslinjer enn det jeg gjør, og Nebu... er en av dem
(Er gjerne litt latskap fra min side, vil ikke tegne fortegnslinje hvis ikke jeg er "nødt")

[Nebuchadnezzar]

Greit å tegne linjer, når du har program som gjør det for deg =) flott innlegg

[mstud]

Greit å tegne linjer, når du har program som gjør det for deg =) flott innlegg

Så sant, så sant ! Men man kan jo bruke et program til å derivere for seg også

Vil selv ikke gjøre det altså, for da går man glipp av moroen med utregningene... Gjelder også mange integraler, men da bruker jeg oftere prog til å sjekke svaret når jeg har regna selv først...


Takk ^^

[Razzy]

Greit å tegne linjer, når du har program som gjør det for deg =) flott innlegg

Så sant, så sant ! Men man kan jo bruke et program til å derivere for seg også

Vil selv ikke gjøre det altså, for da går man glipp av moroen med utregningene... Gjelder også mange integraler, men da bruker jeg oftere prog til å sjekke svaret når jeg har regna selv først...


Takk ^^

Et fantastisk innlegg mstud, blir jo nesten rørt her!

Da har jeg all informasjon til å løse denne oppgaven på egenhånd, jeg legger ut komplett løsningsforslag senere idag. (ikke det at dere trenger det - men jeg trenger å gjøre det )

Uansett tusen tusen takk!

[mstud]

Et fantastisk innlegg mstud, blir jo nesten rørt her!

Da har jeg all informasjon til å løse denne oppgaven på egenhånd, jeg legger ut komplett løsningsforslag senere idag. (ikke det at dere trenger det - men jeg trenger å gjøre det )

Uansett tusen tusen takk!

Jeg også ... trodde ikke det var såå bra....

Et løsningsforslag kan jo alltids komme til nytte for noen som trenger det om det ikke akkurat er oss Kjenner til den: "Jeg trenger å gjøre det" men dere trenger ikke å få det...

Tusen takk, selv...

[Razzy]

Et fantastisk innlegg mstud, blir jo nesten rørt her!

Da har jeg all informasjon til å løse denne oppgaven på egenhånd, jeg legger ut komplett løsningsforslag senere idag. (ikke det at dere trenger det - men jeg trenger å gjøre det )

Uansett tusen tusen takk!

Jeg også ... trodde ikke det var såå bra....

Et løsningsforslag kan jo alltids komme til nytte for noen som trenger det om det ikke akkurat er oss Kjenner til den: "Jeg trenger å gjøre det" men dere trenger ikke å få det...

Tusen takk, selv...

Tror det har foregått noe korresjon på dette feltet siden sist





Kan oppgaven løses slik? Det skal stå "punktet" i teksten over fortegnsskjemaet.

Det eneste jeg mangler nå er å sette inn x=0 i volumuttrykket på til å begynne med og se hvilket volum jeg får ut. Dette volumet er da det største denne prisma kan ha.

Nå gjelder det bare å ut: Hvor mange prosent av kulevolumet utgjør prismevolumet i dette tilfelle?

Vel maks prismevolum har jeg akkurat funnet og volumet for en kule er oppgitt. Ok da setter jeg funksjonene lik hverandre, setter inn x=0 og løser? Ai ai captain? Eller "tosk razzy"

[tex]$${V_y} = {V_{kule}}$$[/tex]

[tex]$${{3\sqrt 3 } \over {16}}\left( {4{r^2}x - {x^3}} \right) = {4 \over 3}\pi {r^3}$$[/tex]

nei dette var noe tull, jeg skal finne PROSENT. Da må jeg isåfall dele dele prismevolumet på kulevolumet. Jeg må finne kule volumet.