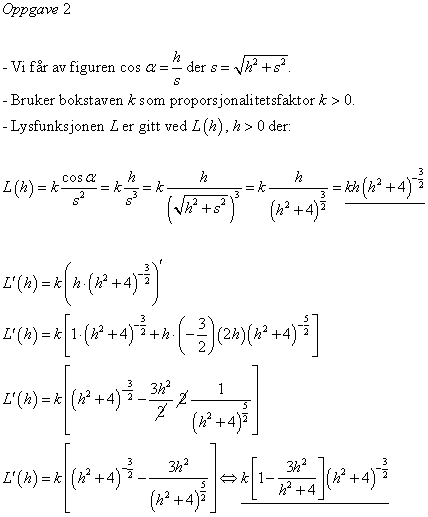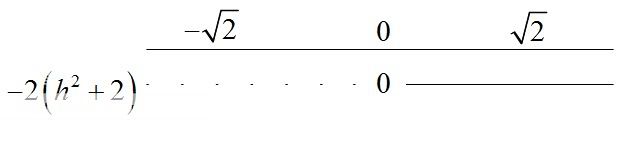Drøfte x-verdi - fortegnslinje

[Razzy]

Hepp hepp!

Her er min deriverte:

[tex]$${k\left[ {1 - {{3{h^2}} \over {{h^2} + 4}}} \right]{{\left( {{h^2} + 4} \right)}^{ - {3 \over 2}}}}$$[/tex]

Den har nullpunktet [tex]$${+\sqrt 2 }$$[/tex] fordi i oppgaven skal [tex]$$h > 0$$[/tex] og [tex]$$k > 0$$[/tex].

Altså jeg har x-verdien som gjør den deriverte lik null, og nå ønsker jeg å studere denne x-verdien ved bruk av fortegns-skjema (vil ikke derivere en gang til).

[tex]$${k\left[ {1 - {{3{h^2}} \over {{h^2} + 4}}} \right]{{\left( {{h^2} + 4} \right)}^{ - {3 \over 2}}}}$$[/tex]

Hver av disse faktorene må inn i utgangspunktet inn i et fortegns-skjema. Ble bare litt satt ut når jeg skulle fylle dem inn:



Legger ved oppgaven:

[Nebuchadnezzar]

[tex](h^2+4)[/tex] er alltid positiv. Følgelig er også [tex](h^2+4)^{-2/3}[/tex] alltid positiv.

Faktoriser vi første leddet så ser vi at vi får (som sikker du også har fått)

[tex]\frac{-2h^2 +4}{h^2+4}[/tex]

Ser vi at nevneren alltid er positiv, og trenger derfor i all hovedsak bare drøfte teller.

[Razzy]

[tex](h^2+4)[/tex] er alltid positiv. Følgelig er også [tex](h^2+4)^{-2/3}[/tex] alltid positiv.

Faktoriser vi første leddet så ser vi at vi får (som sikker du også har fått)

[tex]\frac{-2h^2 +4}{h^2+4}[/tex]

Ser vi at nevneren alltid er positiv, og trenger derfor i all hovedsak bare drøfte teller.

http://www.wolframalpha.com/input/?i=%5 ... qrt%282%29

Merkelig topp-punkt.


Neeh ikke heelt riktig dette...


Telleren her blir jo alltid negativ?

[tex]\frac{-2h^2 +4}{h^2+4}[/tex]

[Nebuchadnezzar]

[tex]-2h^2+4 = 2\left( 2 - h^2\right) = 2\left( \sqrt{2}^2 - h^2\right) = 2\left( \sqrt{2}-h\right)\left( \sqrt{2}+h\right)[/tex]

[tex]-2(h^2 + 2) \neq -2h^2+4 [/tex]

[Razzy]

[tex]-2h^2+4 = 2\left( 2 - h^2\right) = 2\left( \sqrt{2}^2 - h^2\right) = 2\left( \sqrt{2}-h\right)\left( \sqrt{2}+h\right)[/tex]

[tex]-2(h^2 + 2) \neq -2h^2+4 [/tex]

Takk... Da holdt det for i kveld!

Fortsatt god kveld Nebu, du har hodet klart alltid du

[mstud]

Bare for å blande meg inn

Alternativ 1:

[tex]-2h^2+4 = 2\left( 2 - h^2\right) = 2\left( \sqrt{2}^2 - h^2\right) = 2\left( \sqrt{2}-h\right)\left( \sqrt{2}+h\right)[/tex]

[tex]-2(h^2 + 2) \neq -2h^2+4 [/tex]

Alternativ 2: [tex]-2h^2+4=-2(h^2-2)=-2(h-\sqrt{2})(h+\sqrt {2})[/tex]


Altså to mulige faktoriseringer... ^^

Velg den du liker best, hehe

Nebuchadnezzars er lettest å tegne fortegnslinje med da, men den andre er også mulig å bruke.