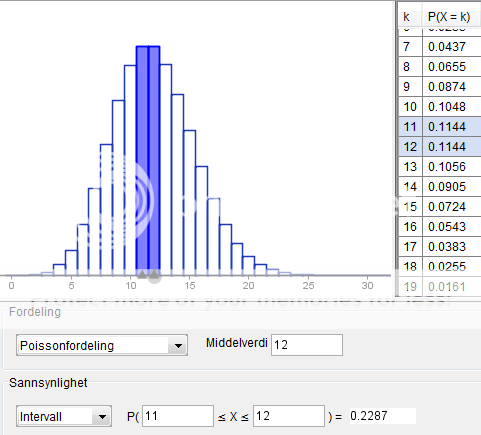
Sannsynlighetskalkulatoren i GeoGebra gir:
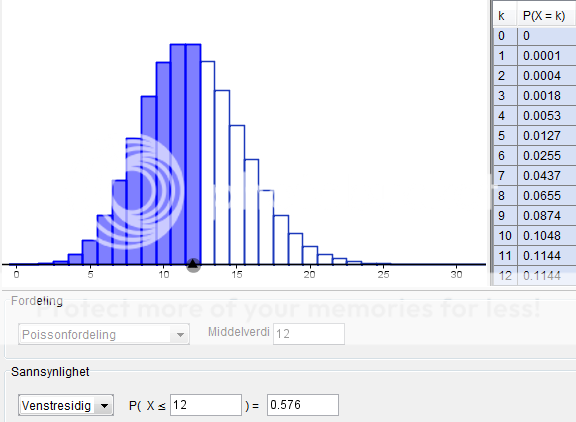
Mitt spørsmål:
[tex]$$P\left( {10 < Y \le 12} \right) = P\left( {Y \le 12} \right) - P\left( {Y > 10} \right)$$[/tex]
[tex]$$P\left( {10 < Y \le 12} \right) = P\left( {Y \le 12} \right) - \left( {1 - P\left( {Y \le 10} \right)} \right)$$[/tex]
[tex]$$ \Rightarrow P\left( {10 < Y \le 12} \right) = {\rm{0}}{\rm{.576}} - 0.6528 = - \;...$$[/tex] (dette må jo være feil)
[tex]$$P\left( {Y > 10} \right)$$[/tex] må være lik: [tex]$$\left( {1 - P\left( {Y \le 10} \right)} \right)$$[/tex] ??
Finner i boka noe jeg tyder som:
[tex]$$P\left( {Y > 10} \right) = P\left( {Y \ge 11} \right)$$[/tex] (som fører til samme gale svaret...)
Læreren sa kjapt at det var:
[tex]${\rm{P(10 < Y}} \le 12{\rm{)}} = P(Y \le 12) - P(Y > 10) = 0,5760 - 0,4616 = \underline{\underline {0,1144}} $[/tex]
Hvordan kan han skrive at [tex]$$P\left( {Y > 10} \right) = 0.4616$$[/tex] ??

[tex]$P(Y > 10) \ne P\left( {X \le 11} \right)$[/tex] Hvordan kan sannsynligheten for større enn 10 være lik sannsynligheten for mindre enn 11 til og med 11?? Legger ved grafen under (det mener jeg dette må være)

Kan noen løse [tex]${\rm{P(10 < Y}} \le 12{\rm{)}}$[/tex] og forklare meg hvorfor? Er så frustrerende å ikke komme seg videre!