Geometri I
Lengdemål
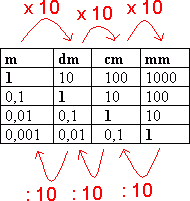
En lengde er gitt ved et måltall og en enhet. Enheten kalles for benevning. Eksempler på enheter er meter (m), desimeter (dm), centimeter (cm) og millimeter (mm). Vi har følgende sammenheng: 1m = 10dm = 100cm = 1000mm
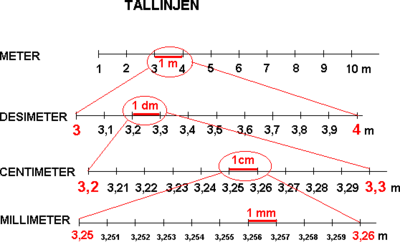
Skal man arbeide med flere lengder er det viktig at alle har samme enhet. Vi går fra en enhet til en mindre enhet ved å multiplisere måltallet med 10. Motsatt vei dividerer vi med 10. Ønsker man for eksempel å gå fra meter til centimeter må man multiplisere med 10 to ganger.
For større lengder har vi enhetene kilometer (km) og mil. 1km = 1000m = 0,1mil. 1 mil = 10km
Du kan selfølgelig gange med 100 en gang, det blir det samme som å gange med 10 to ganger.
\[912mm:10 = 91,2cm \] \[ 91,2cm: 10 = 9,12dm \] \[9,12dm:10=0,912m \]
Areal- flatemål
Et areal er gitt ved et måltall og en enhet. Enheten kalles for benevning. Eksempler på enheter er kvadratmeter <math> [m^2]</math> , kvadratdesimeter <math> [dm^2]</math>, kvadratcentimeter <math> [cm^2]</math> og kvadratmillimeter <math> [mm^2]</math>. Vi har følgende sammenheng: <math>1m^2 = 100dm^2 = 10000cm^2 = 1000000mm^2</math>
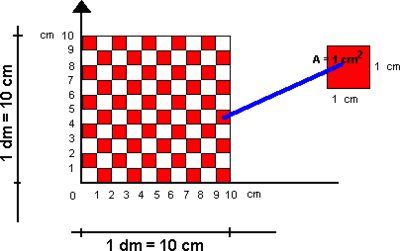
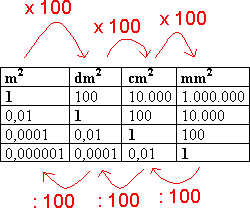
Skal man arbeide med flere areal er det viktig at alle har samme enhet. Vi går fra en enhet til en mindre enhet ved å multiplisere måltallet med 100. Motsatt vei dividerer vi med 100. Ønsker man for eksempel å gå fra kvadratmeter til kvadratcentimeter må man multiplisere med 100 to ganger.
Man ganger med hundre og får <math>1200cm^3</math>
\[ 54000mm ^2:100 = 540cm^2 \] \[ 540cm^2:100 = 5,4 dm^2 \]
For større arealer har vi følgende enheter:
\[ar = 100 m^2, \] \[daa = dekar = 1 000 m^2, \] \[ha = hektar = 10 000 m^2, \] \[ km^2 = kvadratkilometer = 1 000 000 m^2 \]
Volum - rommål
Et volum er gitt ved et måltall og en enhet. Enheten kalles for benevning. Eksempler på enheter er kubikkmeter $ [m^3]$ , kubikkdesimeter <math> [dm^3]</math>,kubikkcentimeter <math> [cm^3]</math> og kubikkmillimeter <math> [mm^3]</math>. Vi har følgende sammenheng: <math>1m^3 = 1000dm^3 = 1000000cm^3 = 1000000000mm^3</math>
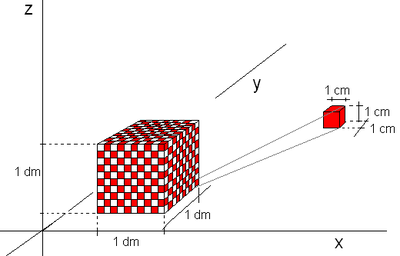
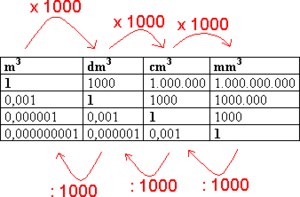
Skal man arbeide med flere volum er det viktig at alle har samme enhet. Vi går fra en enhet til en mindre enhet ved å multiplisere måltallet med 1000. Motsatt vei dividerer vi med 1000. Ønsker man for eksempel å gå fra kubikkmeter til kubikkcentimeter må man multiplisere med 1000 to ganger.
Når man regner ut et volum regner vi med en eller flere lengder. Når det arbeides med flere lengder må alle ha samme enhet. Se avsittet foran, om lengder.
\[ 0,26m^3 \cdot 1000 = 260dm^3 \] \[ 260dm^3 \cdot 1000 = 260000 cm^3 \]
<math>12cm^3:1000= 0,012 dm^3</math>
Fra kubikk til liter - og motsatt
Du trenger kun å huske en ting:
1 liter = <math>1 dm^3</math>.
Nedenfor finer du en tabell som viser samenhengen.
| hl | l | dl | cl | ml | <math>m^3</math> | <math>dm^3</math> | <math>cm^3</math> | <math> mm^3</math> | |
| 1 | 100 | 1000 | 10 000 | 100 000 | 0,1 | 100 | 100 000 | 100 000 000 | |
| 0,01 | 1 | 10 | 100 | 1000 | 0,001 | 1 | 1000 | 1000 000 | |
| 0,001 | 0,1 | 1 | 10 | 100 | 0,0001 | 0,1 | 100 | 100 000 |
112 cl er 1,12 liter som er 1,12<math>dm^3</math>
Thor fyller bensintanken på mopeden med 7500 kubikkcentimeter bensin. Hvor mange liter er det?
<math> 7500cm^3=7,5dm^3=7,5l</math>
Punkt
Et punkt markeres med et kryss. Punktet P kan markeres slik:
Linjer
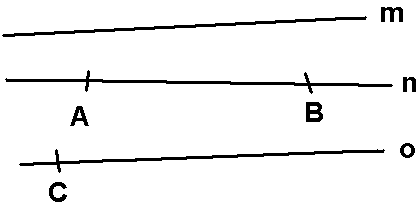
Linjen m har uendelig utstrekning, den fortsetter i begge retninger. Linjestykket AB ligger på linjen n. Linjen n er uendelig lang, men linjestykket AB har en målbar lengde. Linjen o er uendelig lang, det er også linjestrålen som slutter i C.
Dette kan markeres slik:
Parallelle Linjer
Dersom linjen l er parallell med linjen m betyr det at disse to linjene aldri vil krysse hverandre. Vi skriver det slik:
m || n
Linjene kan se slik ut:

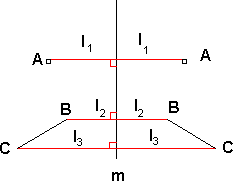
Dersom linjene er parallelle betyr det at avstanden mellom dem er den samme hele veien. Det betyr at avstanden b1 er den samme som b2.
Vinkler
Rette linjer som ikke er parallelle vil før eller siden krysse hverandre (i planet). Da vil de danne en vinkel. Symbolet for en vinkel er<math>\angle </math> . Dette tegnet må ikke forveksles med < som betyr "mindre enn". Vinkelen ABC kan skrives slik: ABC, eller noen ganger bare som B. Vinkelen kan se slik ut:
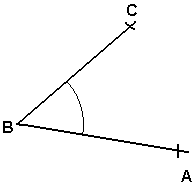
En vinkel består av to vinkelbein og et toppunkt. Toppunktet er der hvor vinkelbeina møtes (eller krysser hverandre). AB og BC er vinkelbein og B er toppunktet. I denne figuren kunne vi kalt vinkelen for B, men vi skal senere se at vi av og til må kalle vinklene med vinkelbein, altså ABC, for å unngå missforståelser.
Lengde måles i meter og tid i sekunder eller timer. Vinkler måles i grader. Dette har ingen ting med temperatur å gjøre, men symbolet vi bruker er det samme. 30 grader skrives 30º. En sirkel måler 360°. Gradeskiven din (også kalt transportør) kan du bruke når du tegner eller måler vinkler. Den går vanligvis opp til 180°.
Det er forskjellige navn på forskjellige typer vinkler. Vi skal se på disse.
Definisjoner:
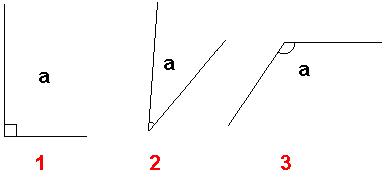
1: Rett vinkel, er en vinkel som er 90°. Kalles også for 90 graders vinkel.
2: Spiss vinkel, er en vinkel som er mindre enn 90º.
3: Stomp vinkel, er en vinkel som er større enn 90º.
Nabovinkler
Summen av to nabovinkler er 180º
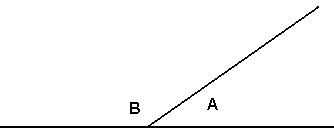
Toppvinkler
Når to linjer krysser hverandre dannes det fire vinkler som parvis er like store.

Samsvarende vinkler
Vinkler som har forskjellig toppunkt, men et vinkelbein felles, kalles samsvarende vinkler.
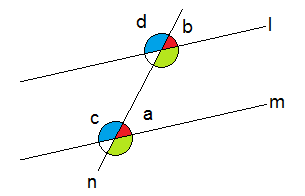
Dersom man vet, eller kan vise at linjen l er parallell med linjen m er vinkel a lik vinkel b, vinkel c lik vinkel d, osv.
Speiling & symmetri
Speiling om en Linje
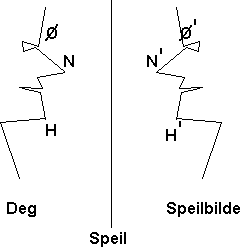
Når du betrakter deg selv i speilet vil du se følgende: Dersom du beveger deg mot speilet, vil speilbildet bevege seg mot deg. Dersom du rygger vil speilbildet trekke seg tilbake. Tenk deg at vi kunne observere dette fra siden, da ville vi ha ditt hode og speilbildet i profil, og speilet ville bare være en strek (fordi vi ser det fra siden). Dette kan se noe slik ut:
Når vi i matematikken skal speile noe om en akse eller linje gjør vi følgende: Vi trekker linjer fra punkt på det objekt som skal speiles. Disse linjene skal stå normalt på linjen man speiler om. Mål avstanden fra punktet på objektet til speilingslinjen. Denne avstanden Legger du så til på andre siden av speilingslinjen. Der merker du av punktet som blir et punkt på speilbildet. Dersom vi har en figur med et punkt A, kaller vi tilsvarende punkt på speilbildet for A'. Dette kan foreksempel se slik ut:
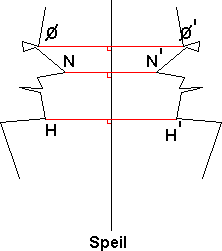
Legg merke till at avstanden fra Ø til speil er lik avstanden fra speil til Ø', avstanden fra N til speil er lik avstanden fra speil til N', osv.
Om vi starter med situasjonen til venstre
blir resultatet av speilingen situasjonen til høyre. Dersom figuren vi skal speile ligger delvis over speilingslinjen kan det se slik ut:

Symmetriakser
Noen eksempler på symmetriakser er vist nedenfor. Vi observerer at forskjellige former har forskjellig antall symmetriakser.
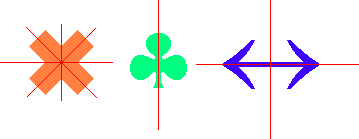
Dersom vi bretter disse figurene langs en symmetriakse, de røde strekene, ser vi at delene på hver side av aksen vil overlappe hverandre fullstendig.
Speiling om et Punkt
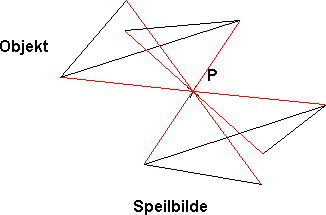
Når vi speiler om et punkt trekker vi linjer fra objektet som skal speiles, gjennom punktet. Avstanden fra objektet til punktet er lik avstanden fra punktet til speilbildet.
Eks:
Kongruente Former
Geometriske figurer som dekker hverandre helt når vi legger den oppå hverandre kalles for kongruente. Det kan tenkes at vi må rotere figurene for at de skal dekke hverandre.

Dersom figur B roteres 90º med klokka, ser vi at figur A og B dekker hverandre helt. A og B er kongruente figurer.
Trekanter
En trekant har tre vinkler og tre sidekanter.
Vinkelsummen i en trekant er 180°
\[A + B + C = 180°\]
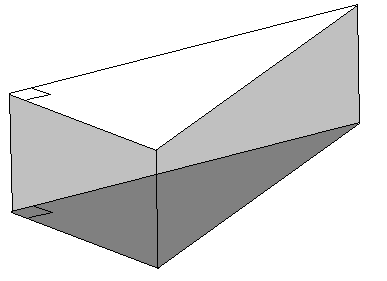
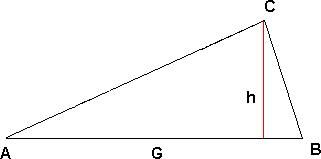
Arealet av en trekant er:
\[Areal = \frac{Gh}{2}\]
Der G er grunnlinja og h er høyden av trekanten.
Figuren under viser hvorfor formelen for arealet er slik.

Rettvinklet Trekant
En rettvinklet trekant består av to kateter og en hypotenus. Begge katetene vil alltid utgjøre vinkelbeina i den rette vinkelen. Hypotenusen vil alltid være den lengste siden i trekanten.
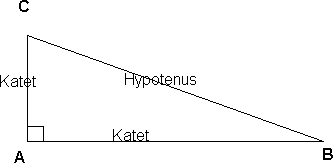
En rett vinkel er 90 grader og markeres som vist i A.
Arealet av en rettvinklet trekant er katet ganger katet delt på to. Fordi det ene katetet gir høyden i trekanten, og det andre grunnlinjen. Det er selvsagt mulig å bruke hypotenusen som grunnlinjen, men det vil ogfe føre til noe mer komplisert regning fordi man da må finne høyden fra hypotenusen til motstående vinlel.
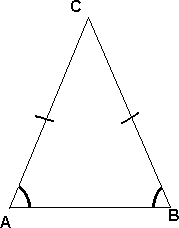
Likebeint Trekant
Dersom to av sidene i en trekant er like lange er trekanten likebeint. "Pinnene" på sidene AC og BC markere at disse sidene er like lange. Når to sider i en trekant er like lange medfører det at to vinkler er like store. I dette eksempelet er vinkel A og vinkel B like store.
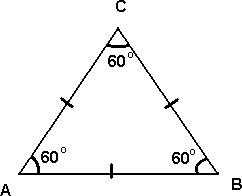
Likesidet Trekant
I en likesidet trekant er alle sidene like lange og alle vinklene er 60°
Pythagoras
Pythagoras setning kan i hovedsak brukes til tre ting;
1. finne lengden av hypotenusen i en rettvinklet trekant
I en rettvinklet trekant er arealet av kvadratet på hypotenusen lik summen av arealet til kvadratene på katetene.
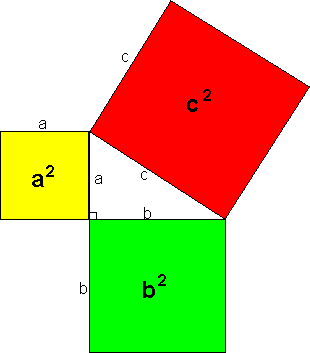
Kvadratet utspent av hypotenusen er lik summen av kvadratene utspent av katetene.
Setningen gjelder kun for rettvinklede trekanter.
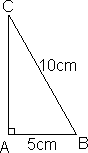
Hva er lengden av AC?
\[ (AB)^2 +(AC)^2 = (BC)^2 \]
\[(5cm)^2 + (AC)^2 = (10cm)^2 \] \[25cm^2 + (AC)^2 = 100cm^2 \] \[AC = \sqrt {75cm^2} = 8,7 cm \]
Eksempel 10: (begge kateter kjent)
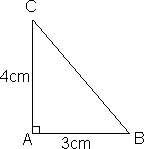
Hva er lengden av BC? \[(AB)^2 +(AC)^2 = (BC)^2 \] \[(3cm)^2 + (4cm)^2 = (BC)^2 \] \[9cm^2 + 16cm^2 = (BC)^2 \] \[BC = \sqrt {25cm^2} = 5 cm \]
I en rettvinklet trekant der vinklene er 30° ,60° og 90° vil alltid hypotenusen være dobbelt så lang som det korteste katetet. Det korteste katetet vil alltid være det motstående til vinkelen på 30°. Dette medfører blant annet at vi er i stand til å finne to sider i en rettvinklet trekant, når betingelsene er som over og vi kjenner en side.
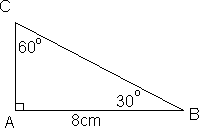
Finn AC og BC.
Siden vi har 30°,60° og 90° i trekanten vet vi at BC = 2 AC. La oss sette AC = x
\[ (AB)^2 +(AC)^2 = (BC)^2 \] \[(8cm)^2 + x^2 = (2x)^2 \] \[ 64cm^2 + x^2 = 4x^2\] \[3x^2 = 64cm^2\] \[x^2 = 21,3cm^2\] \[x=4,6cm \]
AC = 4,6 cm og BC = 9,2 cm.Man kan bruke Pytagoras til å sjekke om en gitt trekant er rettvinklet. Man sjekker om kvadratet utspendt av den lengste siden er lik summen av kvadratene utspendt av de to korteste.
Dersom trekanten er rettvinklet må den lengste siden være hypotenusen. Det betyr at <math>3^2 + 4^2 = 25</math> må være lik <math>5,5^2</math>. Det er ikke tilfellet, derfor er trekanten ikke rettvinklet.
Firkanter
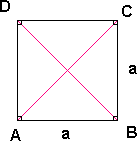
Kvadrat
Et kvadrat er en firkant hvor alle sidene er like lange og alle vinklene er 90°. Diagonalene er markert med røde linjer. En diagonal er en rett linje som går fra et hjørne i firkanten til motstående hjørne. Et kvadrat er et spesialtilfelle av et rektangel.
<math> A = a \cdot a = a^2</math>
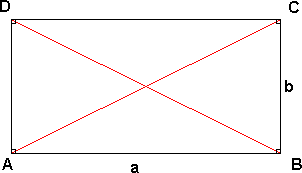
Rektangel
Et rektangel er en firkant der sidene er parvis like lange. Vinklene er 90°.
Arealet av rektangelet er: A = ab
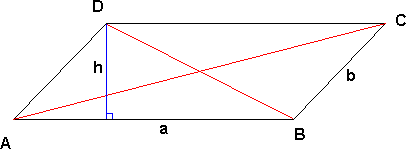
Parallellogram
Et parallellogram er en firkant hvor sidene er parvis parallelle.
Areal:
A = ah
Omkrets
O = 2(a+b)
Rombe
En rombe er en firkant der alle sidene er like lange og parvis parallelle. En rombe er et spesialtilfelle av et parallellogram.
Areal:
A = ah
Omkrets:
Da alle sidene er like lange era = b = c = d
Da blir
O = 4a
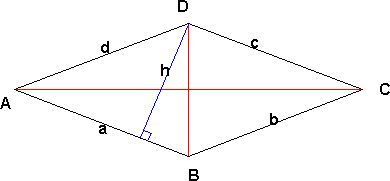
Trapes
I et trapes er to av sidene parallelle.
Areal:
<math> A= \frac{h \cdot (AB+CD)}{2}</math>
Omkrets:
O = AB + BC + CD + DA
Sirkelen
Begreper
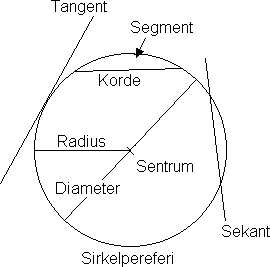
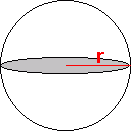
- Sentrum i en sirkel er det punkt hvor avstanden til sirkelbuen eller sirkelperiferien er den samme i alle retninger.
- Sirkelperiferien er en kurve hvor avstanden til sentrum er den samme fra alle punkter på kurven.
- Denne avstanden kalles for radien.
- Diameteren er dobbelt så lang som radien. Diameteren er en rett linje som går fra et vilkårlig punkt P på sirkelbuen, gjennom sentrum av sirkelen, til et punkt på sirkelbuen som ligge på motsattside av P i forhold til sentrum av sirkelen.
- En tangent er en linje som tangerer sirkelperiferien, dvs. den berører kurven i et punkt.
- En korde er en rett linje som går mellom to vilkårlige punkter på sirkelperiferien.
- Området mellom sirkelbuen og korden kalles for et segment.
- En sekant er en linje som skjærer gjennom sirkelperiferien i to vilkårlige punkt.
Du har sikkert mange sirkelformede gjenstander hjemme, bøtte, lysestaker, klokker, etc. Om du måler omkretsen og diameteren på en av disse sirklene og deler omkretsen på diameteren vil du få et svar som er ca. 3,14. Dersom du gjør det samme med alle de andre sirklene, uansett størrelse, vil du få samme resultat.
Dersom du var veldig nøyaktig og hadde superdupert nøyaktige instrumenter ville du fått 3,1415926... Dette tallet brukes mye i matematikken. Vi kaller det for Pi, tegnet vi bruker er dette: <math>\pi</math>
Sirkler tilhører en gruppe kurver som vi kaller for kjeglesnitt. Andre kurver som også tilhører denne gruppen er ellipser, parabler og hyperbler.
Omkrets
Vi har vist at omkretsen O, av en sirkel er gitt ved:
der r er radius i sirkelen.
Areal
Arealet av en sirkel er gitt ved:
<math>A= \pi r^2</math>Der r er radius i sirkelen.
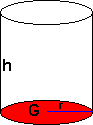
Volum og Overflate
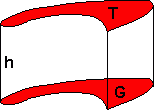
Dersom grunnflaten G og toppflaten T er to parallelle, kongruente plan er volumet gitt ved:
V = Grunnflate · høyde = G · h
Legemets overflate er gitt ved:
O = 2 · Grunnflate + Omkrets Av Grunnflate · høyde
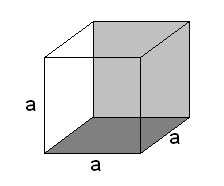
Terning
En terning, eller kube, er en romfigur som avgrenses av seks kvadratiske flater. En terning er et spesialtillfelle av et prisme. Alle sidekantene har derfor samme lengde. Dersom sidekantene av terningen er lik a, kan terningen se slik ut:
Overflaten av en terning blir summen av de seks kvadratenes areal:
<math>O = 6a^2</math>
<math>O = 6 \cdot (6cm)^2 = 216cm^2</math>
Eksempel 16:
<math>O = 6a^2 \Rightarrow a = \sqrt{\frac O6} = \sqrt{ \frac{432cm^2}{6}}= 8,5cm</math>
Volumet av en terning er lengde ganger bredde ganger høyde. Siden disse har samme lengde kan vi skrive volumet som:
<math>V = a\cdot a \cdot a = a^3</math>
<math>V = a\cdot a \cdot a = a^3 = (2cm)^3 = 8cm^3</math>
<math>V = a\cdot a \cdot a = a^3 \Rightarrow a= \sqrt[3] V = \sqrt[3]{125cm^3}= 5cm</math>
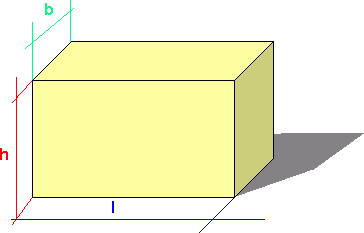
Prisme
Et prisme er en romfigur der grunnflate og toppflate er like, og med rektangulære sideflater som står vinkelrett på grunnflaten. Det finnes altså prismer med svært forskjellig form. Et rett firkantet prisme kan se slik ut:
Arealet av prismets grunnflate er lengde gange bredde. Når vi multipliserer arealet av grunnflaten med høyden, finner vi volumet.
Grunnflate = lengde · bredde = l · b
Volum : V = Grunnflate · h = l · b · h
(Hva man kaller for bredde, lengde og høyde spiller egentlig ingen rolle, for et rett firkantet prisme. Det kommer jo an på hvordan prismet står eller ligger. Grunnflaten er den siden som vender ned mot jorden)
<math>V = l \cdot b \cdot h \Rightarrow l = \frac{V}{bh}= \frac{200cm^3}{2cm \cdot 5cm} = 20cm</math>
Et rett firkantet prisme er avgrenset av flater hvor to og to er like. Overflaten blir:
Overflate: O = 2lb + 2lh + 2bh
Et firkantet prisme har høyden 12cm. Sidene i grunnflaten er henholdsvis 10cm og 20 cm. Hva er overflaten av prismet?
\[ O = 2 \cdot 10cm \cdot 20cm + 2 \cdot 10cm \cdot 12cm + 2 \cdot 20cm \cdot 12cm = \] \[ 400cm^2 + 240cm^2 + 480cm^2 = 1120cm^2\]
Dette er også et prisme:
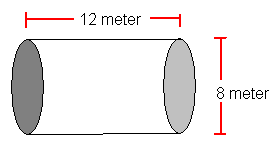
Sylinder
Volum:
Eksempel 22:
<math>V = Gh= \pi \cdot r^2 \cdot h = \pi \cdot (5cm)^2 \cdot 20cm = 1570,8 cm^3 = 1,57 dm^3 = 1,57 liter </math>
Overflate:
Man regner her med at sylinderen har et lokk, altså en overflate på toppen også. Dersom den ikke har det blir overflaten:
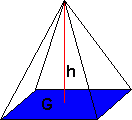
Pyramide
Volum:
<math>V= \frac 13 Gh = \frac 13 \cdot (4,0 cm \cdot 2,0 cm)\cdot 10,0 cm = 26,7cm^3 </math>
<math>V= \frac 13 Gh \Rightarrow G = \frac{3V}{h} = \frac{3 \cdot 30cm^2}{12,0cm} = 7,5cm^2 </math>
Ved å ta kvadratroten av <math>7,5cm^2</math> finner man at sidene i kvadratet er 2,7cm.
Overflaten av en pyramide er summen av alle sidenes areal.
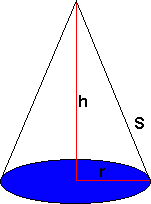
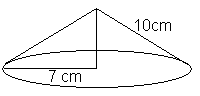
Kjegle
Volum:
<math>V = \frac{1}{3}\pi r^2h = \frac 13 \pi (5cm)^2 \cdot 12cm = 314 cm^3</math>
<math>V = \frac{1}{3}\pi r^2h \quad \Rightarrow \quad 400cm^3 = \frac{1}{3}\pi r^2 \cdot 4cm \quad \Rightarrow \quad r^2 = \frac{3 \cdot 400cm^3}{4cm}\quad \Rightarrow \quad r= 17,3 cm </math>
<math>V= \frac 13 \pi r^2h \Rightarrow h = \frac{3V}{\pi r^2} \Rightarrow h =\frac{3 \cdot 300cm^3}{\pi 36cm^2}= 8cm </math>
Overflate:
<math> s = \sqrt{h^2 + r^2}</math>
<math>V= \frac 13 \pi r^2h = \frac 13 \pi \cdot (7cm)^2 \cdot 7,14cm = 366 cm^3</math>
Overflaten blir: <math> 0 = \pi r^2 + \pi rs = \pi \cdot (7 cm)^2 + \pi \cdot 7cm \cdot 10 cm = 374cm^2</math>
Kule
Volum:
<math>V = \frac{4}{3}\pi (4cm)^3 = 268,1 cm^3 </math>
<math>V = \frac{4}{3}\pi r^3 \\ r = \sqrt[3]{\frac{2V}{4 \pi}} \\ r = \sqrt[3]{\frac{3 \cdot 268,1 cm^3}{4 \pi}} = 4</math>
Overflate:
<math>O = 4 \pi r^2 = 4 \pi (6cm)^2 = 452,4 cm^2 </math>
<math> O = 4 \pi r^2 \\ r= sqrt{ \frac{O}{4 \pi}} \\ r= sqrt{ \frac{400 cm^2}{4 \pi}}= 5,64</math>
d = 2r = 11,3 cm.
Perspektivtegning
Poenget med perspektivtegning er å skape inntrykk av tre dimensjoner (altså av rom og dybde) på et papir eller en annen flate (to dimensjoner). Kunstnerne i renessansen begynte å fatte interesse for dette. Flere italienere arbeidet med emnet og rundt 1480 publiserer Piero della Francesca arbeidet De perspectiva pingendi, der tegning av to og tredimensjonale objekter beskrives. Et annet betydelig arbeid innen emnet stod tyskeren Albrecht Dürer for. Perspektivtegning kommer inn under faget beskrivende geometri som blant annet også omfatter projeksjonstegning.
Begreper
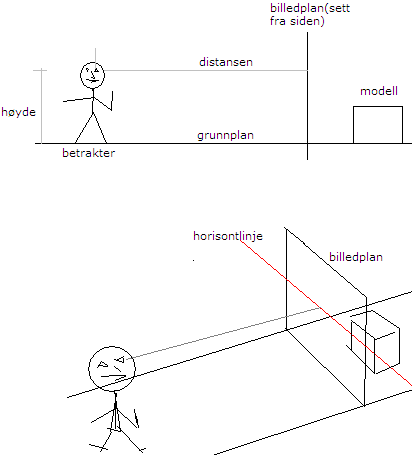
- Billedplan – et tenkt plan man overfører det bildet øye ser, til. Billedplanet er vertikalt. Billedplanet er vinkelrett på synsretningen.
- Grunnplan - "gulvet" betrakteren står på.
- Høyde - avstand fra øye til grunnplan.
- Distansen – avstanden fra øye til billedplan.
- Horisontlinje - linje som representere betrakterens (den som ser) øyehøyde. Alle figurer i dette kapittel har røde horisontlinjer.
- fugleperspektiv - horisontlinjen trukket høyt oppe på arket indikerer at man ser ned på objektet, som en fugl.
- froskeperspektiv - horisontlinjen trukket langt nede på arket indikerer at man ser mye himmel og må se opp på det meste, inkludert objektet som skal tegnes, som en frosk.
- forsvinningspunkt- punkt på horisontlinje der linjer som i virkeligheten er parallelle, møtes.
- Frontperspektiv (sentralperspektiv eller ettpunktsperspektiv) Billedplan står vinkelrett på grunnplan og sideflatene i modellen er vinkelrett på billedplan, dvs. modellen sees rett forfra. Ett forsvinningspunkt.
- Skråperspektiv - med utgangspunkt i frontperspektiv: vri modellen slik at få eller ingen horisontale linjer er parallelle med billedplanet. (de vertikale linjene i modellen er fortsatt parallelle med billedplanet).
- Trepunktsperspektivet - med utgangspunkt i skråperspektivet tiltes billedplanet slik at heller ikke modellens vertikale linjer er parallelle med billedplanet.
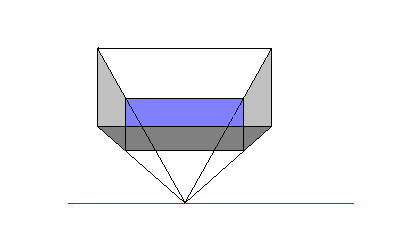
Figuren viser noen begreper tilknyttet perspektivtegning. Modellen, en eske, er plassert med fronten parallell med billedplanet, altså et frontperspektiv.
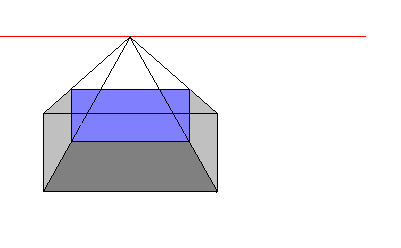
Ettpunktsperspektiv
Alle horisontale linjer parallelle med betraktningsrettningen møtes i et forsvinningspunkt på horisontlinjen. Figur 2 viser esken i et fugleperspektiv, et høyt betraktningsstanpunkt.
I fugleperspektivet ligger horisontlinjen høyt i billedflaten.
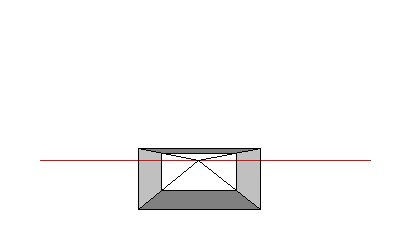
Figuren nedenfor viser samme eske fra et lavt betraktningsstandpunkt, et froskeperspektiv
I froskeperspektiv er horisontlinjen lavt i billedflaten.
Esken sett nesten rett forfra.
For å tegne i frontperspektiv må man først avgjøre betraktningshøyden og avsette horisontlinjen deretter. Høyt betraktningspunkt gir horisont høyt i billedflaten. Lav horisontlinje tilsier et lavt perspektiv, froskeperspektiv.
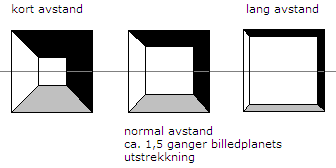
Tegn så fronten av modellen (esken) og marker et punkt på horisontlinjen, rett over (eller under) modellen. Alle linjer som står rettvinklet på billedplanet møtes i dette punkt. Hvor du legger baksiden av esken kommer an på dens form og på avstanden du betrakter den fra. Dersom modellen betraktes på kort avstand gir det en dramatisk perspektiv effekt i forhold til om den betraktes på lang avstand.
Perspektivet påvirkes av avstanden mellom øye og modell. Lang avstand gjør at perspektivet "flates ut", mens kort avstand gir en dramatisk effekt, som en vidvinkel fotolinse.
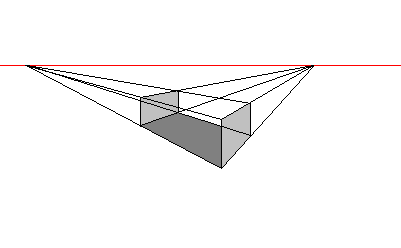
Topunktsperspektiv
Alle horisontale linjer møtes i to punkter på horisontlinjen. Øyet er normalt på vertikale linjer.
Begynn med å bestemme høyden modellen betraktes fra. Reglene for froske- og fugleperspektiv er de samme som for ettpunktsperspektivet.
Avsett to punkter på horisontlinjen. Tegn så den / de vertikale linjene på modellen som ligger nærmest billedplanet. Fra denne / disse knytter du opp alle horisontale linjer til de to punktene på horisontlinjen.
Virkelige horisontale linjer møtes i punktene på horisontlinjen. De linjene som møtes i det ene punktet står i virkeligheten normalt på de linjene som møtes i det andre.
Topunkts fugleperspektiv.
Topunkts froskeperspektiv.
Trepunktsperspektiv
Alle horisontale linjer møtes i to punkter på horisontlinjen. Alle vertikale linjer møtes i et punkt over eller under modellen.
Trepunktsperspektiv.
Isometrisk perspektiv
Dersom behovet for dybdevirkning er begrenset kan man benytte isometrisk perspektiv. Dette er egentlig ikke perspektiv da alle linjer er parallelle. De møtes altså ikke i et punkt i horisonten.
En isometrisk tegning viser to sider av et objekt, I tillegg til topp eller bunn. Alle vertikale linjer tegnes vertikalt. Alle horisontale linjer tegnes med 30º vinkel I forhold til horisonten.
Figuren viser en trapp tegnet på isometrisk papir.
Arkitekter bruker ofte isometriske tegninger når de skal presentere sine arbeider. Isometrisk papir kan du laste ned her: [1]
Konstruksjon med passer
Mye av konstruksjoner foregår i dag ved hjelp av CAD programmer eller Geogebra og lignende programvarer. I enkelte sammenhenger er det greit å kunne noen med passer og linjal. Her er en smakebit.
Vinkelkonstruksjon
Når du tegner en vinkel kan du bruke gradeskive og linjal. Når du skal konstruere en vinkel må du bruke en passer og linjal.
Konstruksjon av 60°.
1. Tegn en linje og avsett et punkt (A), der du ønsker toppunktet.
2. Slå en bue rundt punktet (A). Der buen krysser linjen har du laget et nytt punkt (B).
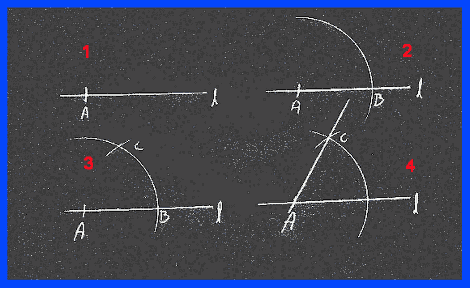
3. Sett passerspissen i B og lag et punkt (C) på buen. Det er viktig at du bruker SAMME ÅPNING på passeren nå, som du brukte på buen.
4. Trekk linjen mellom punktene A og C og du har konstruert en 60 graders vinkel.
Konstruksjon av 90°.
1. Tegn en linje.
2. Avsett et punkt (A) der du ønsker vinkelens toppunkt.

3. Sett passerspissen i punktet (A) på linjen og slå en liten bue på hver side av A, på linjen. Punktene kaller vi for B og C, for å forenkle forklaringen.
4. Sett passerspissen i B og slå en bue som går "over" A. Det er viktig at gapet på passeren er lengre enn avstanden A - B.
5. Gjør det samme i C.
6. Trekk linjen og du har konstruert en vinkel på 90 grader.
Halvering av vinkler.
Alle vinkler kan lett deles i to på følgende måte:

Sett passerspissen i vinkelens toppunkt og slå en liten sirkelbue på hvert av vinkelbeina.
Sett passerspissen i hvert av punktene på vinkelbeina og slå en liten bue.
Trekk en linje mellom punktet der buene krysser hverandre og toppunktet.
Du har nå delt vinkelen i to.
Vi har lært å konstruere 60°, 90° samt å halvere vinkler. Det gjør oss i stand til å konstruere, blant andre, følgende vinkler:
| <math>180^{\circ}</math> | <math>120^{\circ}</math> | <math>105^{\circ}</math> (45 + 60) |
| <math>90^{\circ}</math> | <math>60^{\circ}</math> | <math>75^{\circ}</math> (45 + 30) |
| <math>45^{\circ}</math> | <math>30^{\circ}</math> | <math>67,5^{\circ}</math> (45 + 22,5) |
| <math>22,5^{\circ}</math> | <math>15^{\circ}</math> | <math>52,5^{\circ}</math> (30 + 22,5) |
| <math>7,5^{\circ}</math> | <math>37,5^{\circ}</math> (30 + 7,5) |
Normaler
En normal er en linje som står 90° på en annen linje. De to linjene danner en rett vinkel. Det matematiske symbolet for en normal er . Det finnes tre typer normaler. Disse er:
Midtnormal
En midtnormal er en linje som deler et linjestykke i to like store deler. Vi har allerede lært å konstruere 90° vinkler. Metoden er stort sett den samme:

Vi har linjestykket AB. Sett passerspissen i A og slå en bue. Det er viktig at buen strekker seg over midten av linjestykket slik at vi får de to punktene vi trenger for å kunne trekke normalen.
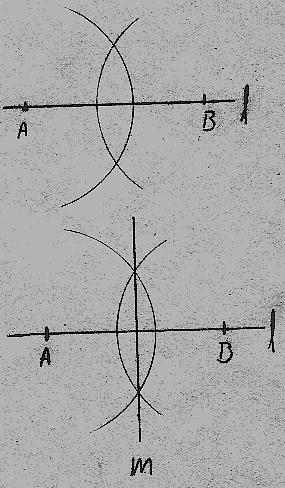
Vi flytter så passerspissen til B og gjør det samme, med samme åpning på passeren. Vi har nå to punkter, et over og ett under linjen l, og kan trekke normalen m. Alle punkter på normalen m ligger like langt fra punktene A og B. m står normalt på l.
Normalen gjennom et punkt ned på linjen
Framgangsmåten er den samme som figuren "Konstruksjon av 90° " viser.
Normalen Til En Linje Gjennom Et Punkt Utenfor Linjen
Vi bruker blant annet denne konstruksjonen til å finne den korteste avstand mellom et punkt og en linje.
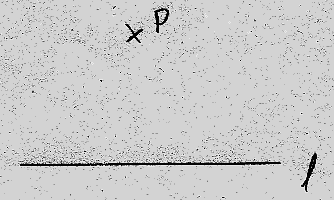
Dette er situasjonen. Vi skal konstruere normalen til linjen l. Normalen skal gå gjennom punktet P.
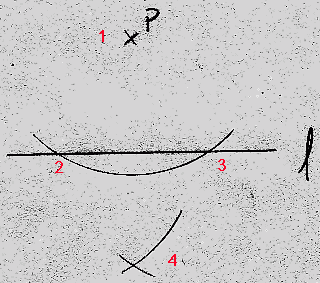
Vi begynner med å sette passerspissen i punktet P (1).
Slå en sirkelbue som krysser linjen l på to steder (2 og 3). Disse to punktene ligger begge like langt fra P.
Vi setter passerspissen i det ene punktet (2) og slår en bue på motsatt side av linjen i forhold til P (4).
Deretter gjør vi det samme i det andre punktet (3).

Vi trekker linjen mellom punktene og oppgaven er løst.
Trekant Og Firkantkonstruksjon
Du har nå lært å konstruere vinkler og normaler. Det betyr at du også kan konstruere trekanter og firkanter og andre figurer.
Når du skal konstruere skal du alltid tegne en prøvefigur først.
En prøvefigur trenger ikke ha riktige mål, men må være så god at den gir deg en forståelse av problemet.
Eks 1:
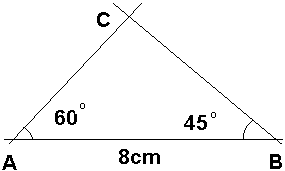
Konstruer en trekant ABC der AB er 8cm. A = 60° og B= 45°.
PRØVEFIGUR:
Tegn alltid prøvefigur først.
OPPGAVELØSNING (konstruksjon):
(1) Avsett linjestykket AB = 8cm.
(2) Konstruer 60° i A.
(3) Trekk linjen mellom A og det konstruerte punkt.
(4) Konstruer 90° i B.
(5) Halver de 90° i B og trekk linjen til den møter linjen fra A. Der ligger punkt C.
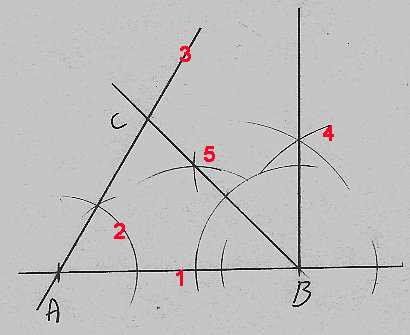
Eks 2:
Konstruer en firkant ABCD, der B er 90° , BAC =30°, AC = 8cm, CD = 4cm og AD = 7cm.
PRØVEFIGUR:

OPPGAVELØSNING (konstruksjon):
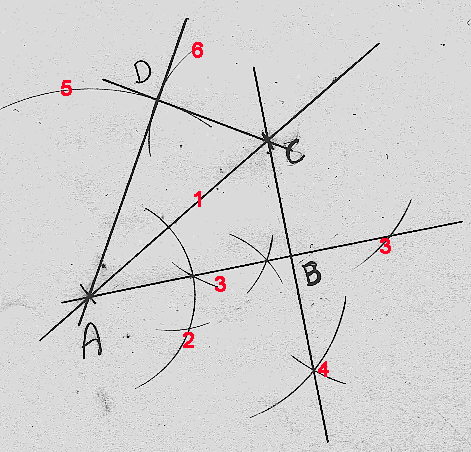
(1) Avsett linjestykket AC =8cm.
(2) Konstruer 60° i A. Halver så vinkelen og trekk linjen
(3) Sett passerspissen i C og slå en bue på linjen der B skal ligge.
(4) Sett passerspissen i de to punktene (3) og konstruer normalen gjennom C og ned på linjen.
(5) Mål gapet på passeren til 7cm, sett den i A og slå en bue,
(6) Mål 4cm i passergapet, sett den i C og slå en bue. Der sirkelbuene krysser hverandre ligger punktet D. Tegn linjene.
Som du ser er ikke prøvefigurene "riktige" i forhold til målene gitt i oppgavene. Det gjør ikke så mye. Figurene er ment å gi deg en forståelse for problemet, samt hjelpe deg å holde styr på hvilke opplysninger du har brukt etter hvert som du konstruerer. For å kunne konstruere en trekant trenger du alltid tre opplysninger. Som du ser fra eksempel 2 er det ikke alltid opplysningene kommer i den rekkefølgen du trenger dem, da er en prøvefigur spesielt viktig. Normalt vil du få bruk for alle opplysningene du får, men det kan jo tenkes at du også får informasjon du ikke trenger, eller ikke kan bruke.
Studer figuren i eksempel to. Finnes det andre løsninger på problemet? Hvorfor / Hvorfor ikke?