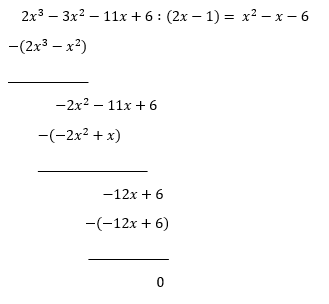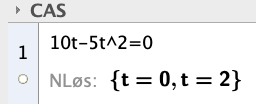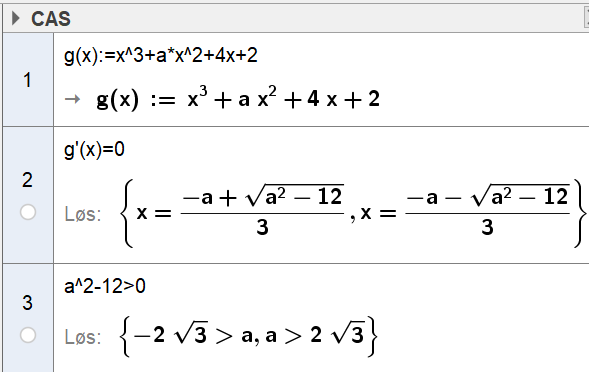R1 2019 vår LØSNING
Løsningsforslag laget av matteprat-bruker SveinR
Løsningsforslag laget av Marius Nilsen ved Bergen Private Gymnas
Diskusjon av denne oppgaven på matteprat
Løsning Del 1 som video av Lektor Håkon Raustøl
Løsning Del 2 som video av Lektor Håkon Raustøl
DEL 1
Oppgave 1
a)
$f(x)=x^3+2x^2-\sqrt{x} \\ f'(x)=3x^2+4x-\frac{1}{2\sqrt{x}}$
b)
$g(x)=x^2\cdot ln(2x-1) \\ g'(x)=2x\cdot ln(2x-1)+\frac{2x^2}{2x-1}$
Brukte produktregelen og kjerneregelen. Løsningen kan evt. faktoriseres.
c)
$ h(x) = \frac{4x}{e^{2x}} \\ h'(x)=\frac{4e^{2x}-4x\cdot 2e^{2x}}{(e^{2x})^2} \\ = \frac{e^{2x}(4-8x)}{(e^{2x})(e^{2x})} = \frac{-8x+4}{e^{2x}}$
Oppgave 2
a)
$\frac{1}{x^2-x}+\frac{1}{x^2+x}-\frac{1}{x^2-1} \\ = \frac{1}{x(x-1)}+\frac{1}{x(x+1)}-\frac{1}{(x+1)(x-1)} \\ = \frac{x+1}{x(x-1)(x+1)}+\frac{x-1}{x(x+1)(x-1)}-\frac{x}{x(x+1)(x-1)}\\ = \frac{x+1+x-1-x}{x(x+1)(x-1)} \\ = \frac{x}{x(x+1)(x-1)} \\ = \frac{1}{x^2-1}$
b)
$\frac{(ln\,e^3+1)^2}{(e^{ln\,3}+1)} = \frac{(3+1)^2}{(3+1)^3}=\frac{4^2}{4^3}=\frac{1}{4}$
Oppgave 3
a)
$(2x-1)=0 \\ x=\frac{1}{2}$
Sjekker om $x=\frac{1}{2}$ er et nullpunkt for $f(x)$:
$f(\frac{1}{2})= 2(\frac{1}{2})^3-3(\frac{1}{2})^2-11\cdot \frac{1}{2}+6 \\ = \frac{2}{8}-\frac{3}{4}-\frac{11}{2}+6 \\ = \frac{2}{8}-\frac{6}{8}-\frac{44}{8}+6 \\ = \frac{-48}{8}+6 = -6+6 = 0$
$x=\frac{1}{2}$ er et nullpunkt for $f(x)$, det vil si at divisjonen $f(x):(2x-1)$ går opp.
b)
Utfører polynomdivisjonen $f(x) : (2x-1)$
$x^2-x-6=(x-3)(x+2)$
$f(x)=(2x-1)(x-3)(x+2)$
c)
$f(x) \geq (2x-1)(x+2) \\ (x-3)(2x-1)(x+2) \geq (2x-1)(x+2) \\ (x-3)(2x-1)(x+2) - (2x-1)(x+2) \geq 0$
Setter felles faktor $(2x-1)(x+2)$ utenfor parentes.
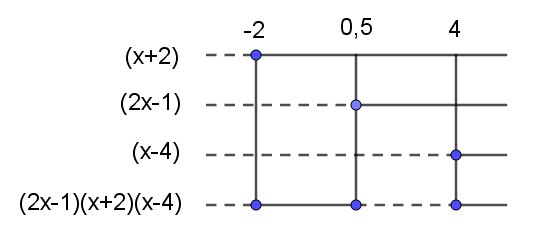
$ (2x-1)(x+2)((x-3)-1) \geq 0 \\ (2x-1)(x+2)(x-4) \geq 0 $
$f(x) \geq (2x-1)(x+2)$ når $x \in [-2, \frac{1}{2}] \cup [4,\rightarrow \rangle$
Oppgave 4
a)
Vi har punktene $A(1,3)$ og $B(5,-1)$
$\vec{AB}=[5-1,-1-3]=[4,-4]$
$|\vec{AB}|=\sqrt{4^2+(-4)^2}=\sqrt{32}=\sqrt{2\cdot 16}=4\sqrt{2}$
b)
Likning for en sirkel med sentrum i $(x_0, y_0)$:
$ (x - x_0)^2 + (y - y_0)^2 = r^2 $
Husk at sirkelens diameter er fra punkt A til punkt B. Sentrum i vår sirkel blir midt mellom punkt A og B, i (3,1).
Radius blir halvparten av $|\vec{AB}|$: $\frac{4\sqrt{2}}{2}= 2\sqrt{2}$
Vi setter inn våre verdier og får likningen for sirkelen:
$ (x - 3)^2 + (y - 1)^2 = (2\sqrt{2})^2 \\ (x-3)^2 + (y-1)^2 = 4\cdot 2 \\ (x-3)^2 + (y-1)^2 = 8 $
c)
For å få en rett vinkel i C, må punkt C ligge på sirkelperiferien. Dette på grunn av Thales setning.
Sentrum av sirkelen er i punkt (3,2), og radiusen av sirkelen er $2\sqrt{2}$. Siden $3+2\sqrt{2} < 6 $, så tangerer ikke linja x=6 sirkelen. Dermed er punkt C utenfor sirkelperiferien, og det er ikke mulig å plassere C slik at trekanten ABC får en rett vinkel i C.
En annen måte å finne ut av det er å sjekke om det finnes en y-verdi for punkt C hvor $\vec{AC}\cdot \vec{BC} = 0$.
Oppgave 5
a)
$\binom{10}{3} = \frac{10 \cdot 9 \cdot 8}{3 \cdot 2 \cdot 1} = 10 \cdot 3 \cdot 4 = 120 $
120 ulike grupper på tre deltakere kan komme til finalen.
b)
Vi har flere kvinner enn menn i en gruppe på tre, dersom vi har to eller tre kvinner.
P(to eller tre kvinner) = $\frac{\binom{5}{2} \binom{5}{1}}{ \binom{10}{3}} + \frac{\binom{5}{3} \binom{5}{0}}{ \binom{10}{3}} = \frac{10 \cdot 5}{120} + \frac{10 \cdot 1 }{120} = \frac{60}{120} = \frac{1}{2}$
60 av de 120 gruppene, det vil si halvparten, inneholder flere kvinner enn menn.
Oppgave 6
a)
Graf A tilhører funksjonen f, og graf B tilhører funksjonen f´. Dette ser vi fordi når f´ har negativ verdi (grafen er under x-aksen), så synker grafen til f. Når f´ har positiv verdi (grafen er over x-aksen), så stiger grafen til f. Videre har den deriverte et nullpunkt der hvor funksjonen f har et ekstremalpunkt (bunnpunkt).
b)
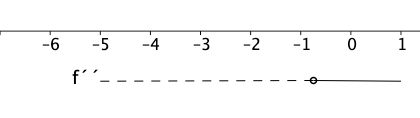
Den dobbelderiverte er negativ for de x-verdiene hvor den deriverte synker, har et nullpunkt i x-verdien til den derivertes bunnpunkt (vendepunktet til f), og er positiv for de x-verdiene hvor den deriverte stiger.
Oppgave 7
a)
$\angle APC$ og $\angle DPB$ er toppvinkler, og derfor like store.
$\angle CAB$ og $\angle CDB$ er periferivinkler som spenner over den samme sirkelbuen. Disse er derfor like store.
Dersom to trekanter har to parvis like store vinkler, er trekantene formlike. $\triangle APC$ og $\triangle PBD$ er derfor formlike.
b)
Siden $\triangle APC$ og $\triangle PBD$ er formlike, har vi at
$\frac{AP}{PD}=\frac{CP}{PB} \Rightarrow AP \cdot PB = CP \cdot PD$
Oppgave 8
a)
$f'(2)=0 \Leftarrow$ Grafen til $f$ har et toppunkt i $(2, f(2))$
Dersom grafen til f har et toppunkt i $(2, f(2))$, impliserer det at vi har $f'(2)=0$. Derimot, hvis vi bare vet at $f'(2)=0$, vet vi ikke om grafen til f har et toppunkt, et bunnpunkt eller et terrassepunkt i $(2, f(2))$. $f'(2)=0$ impliserer altså ikke nødvendigvis et toppunkt i $(2, f(2))$.
b)
$f'(3)=0$ og $f' '(3)>0 \Rightarrow $ Grafen til $f$ har et bunnpunkt i $(3, f(3))$
Dersom $f'(3)=0$ vet vi at grafen til f har et ekstremalpunkt. Dersom $ f' '(3)>0 $ i tillegg, så har vi et bunnpunkt.
Det er derimot ikke alle funksjoner med bunnpunkt i $(3,f(3))$ som har $ f' '(3)>0 $ . For eksempel, dersom $ f(x)=(x-3)^n $ , hvor n er et partall større enn eller lik 4, så er $ f'(3)=0 $ og $ f' '(3)=0 $ i bunnpunktet $(3, f(3))$.
Dette kan være litt vanskelig å vite, og forhåndssensurrapporten til denne eksamen presiserer at ekvivalenspil også blir godtatt dersom man argumenterer godt for svaret sitt.
DEL 2
Oppgave 1
a)
$ \vec{r\,} (t) = [28t-3t^2, 10t-5t^2]$
Bestemmer fartsvektoren:
$ \vec{v\,} (t) = \vec{r\,} '(t) = [28-6t, 10-10t]$
Bestemmer farten da ballen ble sparket:
$ \vec{v\,} (0)=[28,10]$
$|\vec{v\,} (0) | = \sqrt{28^2 + 10^2 } = 29,7 $
Banefarten som ballen fikk da den ble sparket var 29,7 m/s.
b)
Når ballen treffer bakken, er posisjonsvektorens y-koordinat lik 0. Finner tiden t hvor dette skjer i CAS på Geogebra:
Ballen kastes når tiden t=0. Ballen treffer bakken når tiden t=2, etter 2 sekunder.
c)
Når ballen er på sitt høyeste punkt, er fartsvektorens y-koordinat lik 0 (ingen fart i y-retning). Finner tiden t hvor dette skjer:
$10-10t=0 \\ t=1$
Finner ballens banefart, altså fartsvektorens x-koorinat i tiden t=1:
$28-6\cdot 1 = 28 - 6 = 22$
Ballens banefart da den var i sitt høyeste punkt var 22 m/s.
Oppgave 2
a)
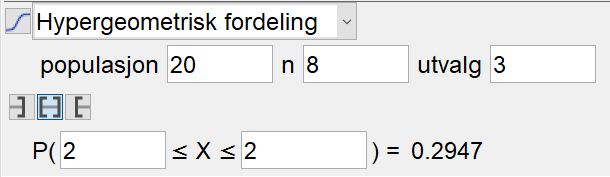
Bruker sannsynlighetskalkulatoren i Geogebra, og velger hypergeometrisk fordeling. 8 av de 20 ansatte er menn, og utvalget er 3.
Sannsynligheten for at nøyaktig 2 av de 3 vinnerne er menn, er 0,2947.
b)
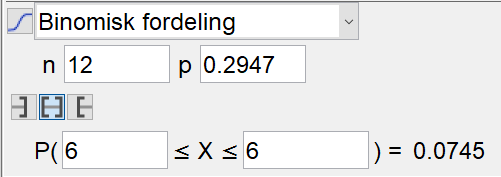
Velger binomisk fordeling, der antall lotterier er 12, og sannsynligheten for at 2 av 3 vinnere er menn, er 02947 (fra forrige oppgave).
Sannsynligheten for at 2 av 3 vinnere er menn i 6 av de 12 lotteriene, er 0,0745 = 7,45%.
c)
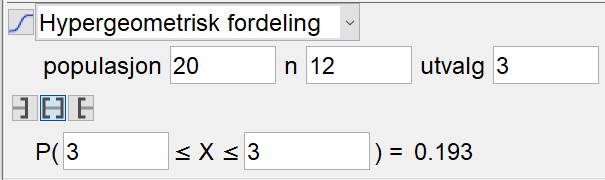
Sannsynligheten for at alle vinnerne i ett lotteri er kvinner er 0,193.
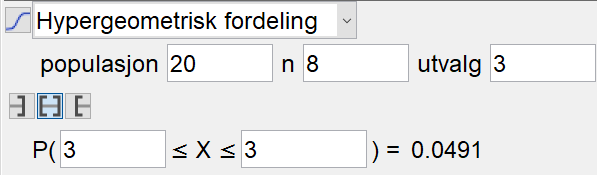
Sannsynligheten for at alle vinnerne i ett lotteri er menn er 0,0491.
Sannsynligheten for at alle vinnerne er av samme kjønn i ett lotteri er da $0,193+0,0491=0,2421$
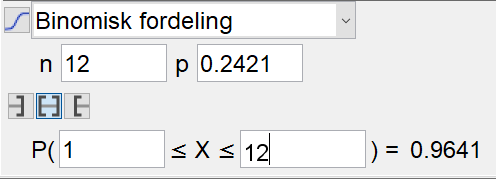
Finner sannsynligheten for at de tre vinnerne har samme kjønn i minst ett av de tolv lotteriene:
Sannsynligheten er 0,9641 = 96,41%.
Oppgave 3
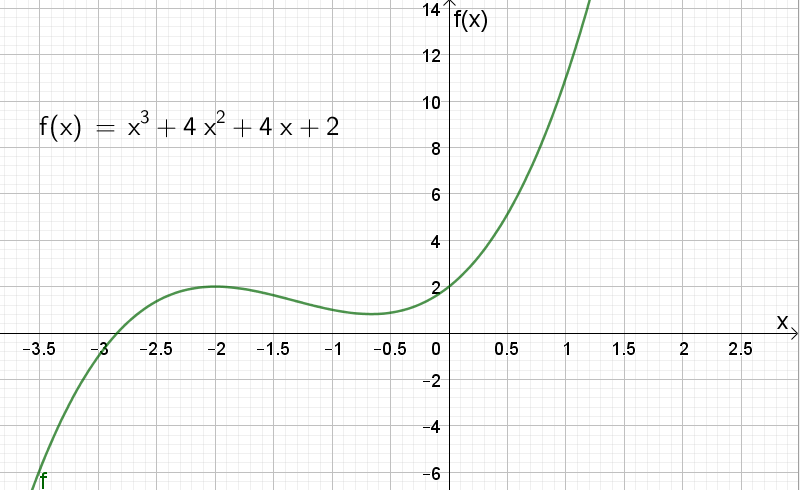
a)
b)
Vi har et toppunkt i $(-2, 2)$, og et bunnpunkt i $(- \frac{2}{3}, \frac{22}{27})$. Siden jeg har tegnet grafen i oppgave a), kan jeg se hva som er topp- og bunnpunkt. Dersom jeg ikke hadde tegnet grafen til $f$, måtte jeg ha sjekket hvor den deriverte er positiv og negativ for å avgjøre hva som er topp- og bunnpunkt (og se at vi f.eks. ikke har et terrassepunkt).
Vendepunktet er i $(- \frac{4}{3}, \frac{38}{27})$
c)
Grafen til $g$ har et toppunkt og et bunnpunkt for $a < -2 \sqrt{3}$ og $a > 2\sqrt{3}$
d)
Finner vendepunktet til $g$ i rad 2. I rad 4 setter jeg inn x-koordinaten til vendepunktet i h(x), og ser at jeg får samme y-koordinat på grafen til $h$ som for vendepunktet til $g$, uansett hvilken verdi $a$ har. I rad 5 bekrefter jeg bare at y-verdien i rad 2 og rad 4 har samme verdi.
Oppgave 4
a)
$\angle ACB$ og $\angle DCG$ er toppvinkler, og derfor like store. Videre er CG = CB siden CBDF er et kvadrat og derfor har like lange sider. På samme måte er CD = AC siden ACDE er et kvadrat. Vi har to parvis like lange sider, med like stor vinkel mellom disse. Trekantene $\triangle ABC$ og $\triangle GDC$ er derfor kongruente.
b)
Vi tenker oss at punkt H er sentrum i en sirkel med diameter AB. På grunn av Thales setning vil punkt C ligge på sirkelen, siden $\angle ACB = 90$ grader, og $\angle AHB = 180$ grader. Da vil AH og HC begge være sirkelens radius, og derfor vil AH=HC. Det betyr at $\triangle AHC$ er likebeint.
c)
Siden trekantene $\triangle ABC$ og $\triangle GDC$ er kongruente, er $\angle CGI$ og $\angle ABC$ like store.
Siden $\triangle AHC$ er likebeint, har vi at $\angle ACH = \angle CAB$. Videre er $\angle ACH = \angle GCI$ siden disse er toppvinkler. Det betyr at $\angle CAB = \angle GCI$.
I $\triangle ABC$ og $\triangle CIG$ har vi to parvis like store vinkler. Altså er trekantene formlike, og $\angle ACB = \angle CIG = 90$ grader.