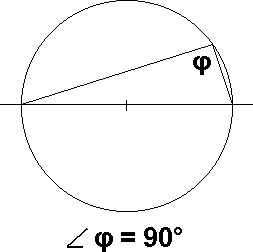Sirkelen II
Begreper
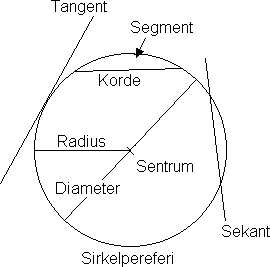
- Sentrum i en sirkel er det punkt hvor avstanden til sirkelbuen eller sirkelperiferien er den samme i alle retninger.
- Sirkelperiferien er en kurve hvor avstanden til sentrum er den samme fra alle punkter på kurven.
- Denne avstanden kalles for radien.
- Diameteren er dobbelt så lang som radien. Diameteren er en rett linje som går fra et vilkårlig punkt P på sirkelbuen, gjennom sentrum av sirkelen, til et punkt på sirkelbuen som ligge på motsattside av P i forhold til sentrum av sirkelen.
- En tangent er en linje som tangerer sirkelperiferien, dvs. den berører kurven i et punkt.
- En korde er en rett linje som går mellom to vilkårlige punkter på sirkelperiferien.
- Området mellom sirkelbuen og korden kalles for et segment.
- En sekant er en linje som skjærer gjennom sirkelperiferien i to vilkårlige punkt.
Du har sikkert mange sirkelformede gjenstander hjemme, bøtte, lysestaker, klokker, etc. Om du måler omkretsen og diameteren på en av disse sirklene og deler omkretsen på diameteren vil du få et svar som er ca. 3,14. Dersom du gjør det samme med alle de andre sirklene, uansett størrelse, vil du få samme resultat.
Dersom du var veldig nøyaktig og hadde superdupert nøyaktige instrumenter ville du fått 3,1415926... Dette tallet brukes mye i matematikken. Vi kaller det for Pi, tegnet vi bruker er dette: <math>\pi</math>
Sirkler tilhører en gruppe kurver som vi kaller for kjeglesnitt. Andre kurver som også tilhører denne gruppen er ellipser, parabler og hyperbler.
Omkrets
Vi har vist at omkretsen O, av en sirkel er gitt ved:
<math>O = 2 \pi r</math>
der r er radius i sirkelen.
Eksempel:
Finn omkretsen i en sirkel med radius 12 cm.
<math>O = 2 \pi r = 2 \cdot \pi \cdot 12cm = 2 \cdot 3,14 \cdot 12 cm =75,36 cm</math>
Areal
Arealet av en sirkel er gitt ved:
<math>A= \pi r^2</math>
Der r er radius i sirkelen.
Eksempel:
Finn arealet i en sirkel med radius 8 cm.
<math>A= \pi r^2 = \pi \cdot (8 cm)^2 = 200,96 cm^2</math>
Buelengde
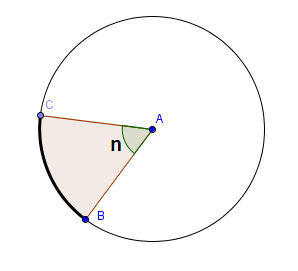
Nedenfor ser du en figur med en sektor med vinkel n. Buelengden av sektoren er avstanden langs sirkelperiferien fra B til C. Buelengden av en sektor er gitt ved:
<math> L = 2 \cdot \pi \cdot r \cdot \frac{n}{360} = \frac{2 \pi r n}{360} </math>
Det er en følge av at en sirkel er delt inn i 360 grader. n er sektorens antall grader.
Sirkelsektor
Arealet av en sirkelsektor er gitt ved:
<math> A = \pi \cdot r^2 \cdot \frac{n}{360} = \frac{n \pi r^2}{360} </math>
Sentralvinkel og periferivinkel
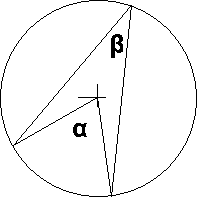
Vinkelen alfa kalles for sentralvinkel fordi den har sitt toppunkt i sirkelsentrum, med vinkelbein som går ut til sirkelperiferien. Vinkelen ß (beta) kalles for en periferivinkel fordi toppunket ligger på periferien. Begge vinkler spenner over samme korde. Vi har da det forhold at:
<math> \alpha =2 \beta</math>
Dette forhold har to viktige implikasjoner.
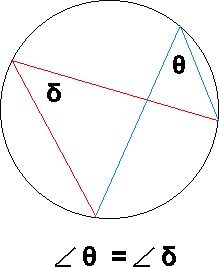
Det ene er at periferivinkler som spenner over samme bue er like store.
Det andre er at periferivinkler på en havsirkel alltid er 90°