S2 2014 høst LØSNING: Forskjell mellom sideversjoner
| (7 mellomliggende sideversjoner av samme bruker vises ikke) | |||
| Linje 367: | Linje 367: | ||
===b)=== | ===b)=== | ||
Dersom Katrine ikke hadde tatt ut 8000 kr hvert år, hadde hun 31. desember 2014 hatt: | |||
$87249 \cdot 1,03^4 = 98200$ kr på kontoen. | |||
Nå kan vi finne ut hva de 4 uttakene på 8000 kr hvert år hadde forrentet seg til dersom hun hadde spart de. | |||
Summen av sluttverdiene blir: | |||
$8000 \cdot 1,03 + 8000 \cdot 1,03^2 + 8000 \cdot 1,03^3 + 8000 \cdot 1,03^4 $ | |||
Dette er en geometriske rekke. $a_1=8000 \cdot 1,03 $ og $k=1,03$. | |||
Jeg bruker sumformelen og regner ut summen vha. CAS: | |||
[[File:S2-H14-Del2-Oppg3b.png]] | |||
31. desember 2014 har Katrine 63726 kr på sparekontoen. | |||
== Oppgave 4 == | == Oppgave 4 == | ||
=== a) === | |||
[[File:S2-H14-Del2-Oppg4a.png]] | |||
=== b) === | |||
Jeg lager en linje for $y=10$. Deretter bruker jeg "skjæring mellom to objekt" til å finne skjæringspunkta mellom den rette linja og grafen til $V$. | |||
Jeg finner skjæringspunkta $(52.7, 10)$ og $(105.2, 10)$. (Sjå figuren i oppg. a)) | |||
I følge modellen vi produksjonen være 10 milliarder fat per år 52,7 år etter 1930 og 105,2 år etter 1930. | |||
Det vil si i løpet av år 1982 og i løpet av år 2035. | |||
=== c) === | |||
Jeg skriver inn i GeoGebra: "Ekstremalpunkt[V, 0, 140]" og finner toppunktet i $(78.9, 15.2)$. (Sjå figuren i oppg. a)) | |||
Produksjonen vil være størst på slutten av år 2008. | |||
=== d) === | |||
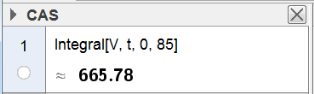
Jeg bruker CAS i GeoGebra til å regne ut det bestemte integralet av $V(t)$ mellom $t=0$ og $t=85$. | |||
[[File:S2-H14-Del2-Oppg4d.png]] | |||
Den totale produksjonen av olje fra om med 1930 til og med 2014 vil være 665,78 milliarder fat. | |||
== Oppgave 5 == | == Oppgave 5 == | ||
=== a)=== | |||
$B_4=35$ | |||
=== b)=== | |||
$$B_n =T_n + T_{n+3} -3 \\ | |||
B_5 = T_5 +T_8 -3 $$ | |||
$$T_n = 1 + 2 + 3 + \cdots n = \sum_1^n n$$ | |||
Jeg bruker CAS til å regne ut dette: | |||
[[File:S2-H14-Del2-Oppg5b.png]] | |||
$B_5 = 48 $ | |||
=== c)=== | |||
Vi kan se at $T_n=1+2+3+\cdots + n$ er summen av en aritmetisk rekke, med $a_1 =1$, $a_n=n$ og $d=1$. | |||
Da kan vi bruke formel for sum av en aritmetisk rekke til å skrive $T_n$ på en annen måte: | |||
$$T_n = \frac{a_1+a_n}{2} \cdot n = \frac{1+n}{2} \cdot n = \frac{(1+n)n}{2} = \frac{n^2+n}{2}$$ | |||
Vi bruker uttrykket for $T_n$ til å finne et uttrykk for $T_{n+3}$: | |||
$$T_{n+3}= \frac{1+(n+3)}{2} \cdot (n+3) = \frac{(n+4)(n+3)}{2} = \frac{n^2+7n+12}{2} $$ | |||
Da får vi: | |||
$$B_n = T_n + T_{n+3} -3 | |||
= \frac{n^2+n}{2} + \frac{n^2+7n+12}{2} -3 | |||
= \frac{n^2+n+n^2+7n+12-6}{2} | |||
= \frac{2n^2 +8n +6 }{2} | |||
= n^2 +4n +3$$ | |||
== Oppgave 6 == | == Oppgave 6 == | ||
=== a) === | |||
Jeg bruker sannsynlighetskalkulatoren i GeoGebra. | |||
Jeg velger "Normalfordeling", og skriver inn "$\mu=0.33$" og "$\sigma=0.03$". | |||
[[File:S2-H14-Del2-Oppg6a.png]] | |||
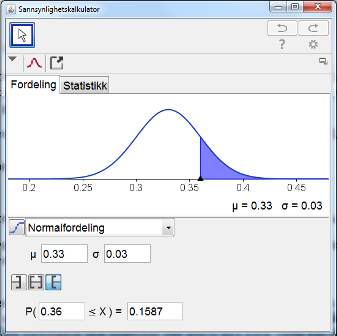
Jeg finner at $P(X>0,36)=0,1587$. | |||
Sannsynligheten for at en tilfeldig valgt kartong inneholder mer enn 0,36 liter er 15,9 %. | |||
=== b) === | |||
Jeg fortsetter med sannsynlighetskalkulatoren: | |||
[[File:S2-H14-Del2-Oppg6b.png]] | |||
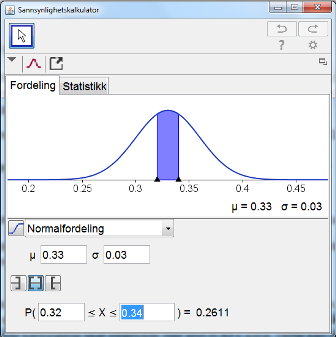
Jeg finner nå at $P(0,32<X<0,34)=0,2611$. | |||
26,1 % av kartongene vil inneholde mellom 0,32 og 0,34 liter. | |||
=== c) === | |||
Jeg setter opp hypoteser: | |||
$H_0: \mu=0,33 \quad$ (Innholdet er riktig) | |||
$H_1: \mu<0,33 \quad$ (Innholdet er for lite) | |||
Vi har testet 25 tilfeldige kartonger, med $\bar{x}=0,292$ liter. | |||
Da er samla innhold for de 25 kartongene: $25 \cdot 0,292$ liter $=7,3$ liter. | |||
Vi går ut fra at $H_0$ gjelder. | |||
Vi lar $X_\Sigma$ være summen av innholdet til 25 tilfeldige kartonger. | |||
Da er $X_\Sigma$ normalfordelt, med | |||
$\mu_{X_\Sigma}= n \cdot \mu = 25 \cdot 0,33= 8,25$ og | |||
$\sigma_{X_\Sigma}= \sqrt{n} \cdot \sigma = \sqrt{25} \cdot 0,03 = 0,15 $ | |||
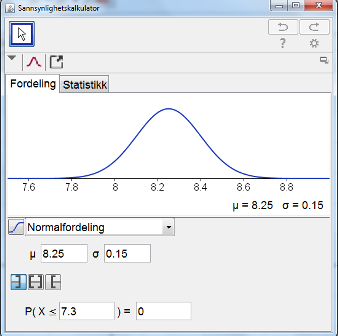
Vi ønsker nå å finne sannsynligheten for at samla innhold til 25 kartonger er mindre enn 7,3 liter, $P(X_\Sigma < 7,3)$. | |||
Jeg bruker sannsynlighetskalkulator i GeoGebra: | |||
[[File:S2-H14-Del2-Oppg6c.png]] | |||
P-verdien blir $P(X_\Sigma ≤ 7,3)=0 $ | |||
P-verdien er $0 \% < 5 \%$. Da kan vi forkaste nullhypotesen. | |||
Vi har grunnlag for å si at bedriften i snitt tapper for lite juice på kartongene. | |||
=== d) === | |||
Vi må finne $z$ slik at $P(Z>z)=0,90$. Så kan vi bruke omregningsformelen til få finne $\mu$. | |||
$P(Z>z)=0,90$ er det samme som at $ P(Z<z)=0,10 $. | |||
Vi finner denne verdien i tabellen for standard normalfordeling. | |||
$z=-1,28$ gir den verdien som er nærmest 0,10. | |||
$$ z = \frac{x-\mu}{\sigma} \\ | |||
-1,28 = \frac{0,32-\mu}{0,03}$$ | |||
Løser likningen vha. CAS: | |||
[[File:S2-H14-Del2-Oppg6d.png]] | |||
Forventningsverdien må være 0,36 liter for at ca. 90 % av kartongene skal inneholde mer enn 0,32 liter juice. | |||
Siste sideversjon per 17. mai 2015 kl. 21:30
Del 1
Oppgave 1
a)
$f(x)=3 \ln(x+2)$
Deriverer ved å bruke kjerneregelen med $u=x+2 \Rightarrow u'=1$
$$f'(x)=3 \cdot \frac{1}{u} \cdot u' = 3 \cdot \frac{1}{x+2} \cdot 1 = \frac{3}{x+2} $$
b)
$g(x)=x \cdot \ln(3x)$
Deriverer ved å bruke produktregelen og kjerneregelen:
$$g'(x)=1 \cdot \ln(3x) + x \cdot \frac{1}{3x} \cdot 3 = \ln(3x) + 1$$
Oppgave 2
Brøken kan forkortes, dersom $(x-3)$ er en faktor i telleren $f(x)=(x^3-2x^2-3x)$.
Fra nullpunktsetningen vet vi at dersom $(x-3)$ er en faktor i polynomet $f(x)$, må $x=3$ være et nullpunkt for $f(x)$.
Vi sjekker dette: $f(3)=3^3-2 \cdot 3^2-3 \cdot 3= 27-18-9 =0$
Brøken kan forkortes.
Vi kan forkorte brøken ved å utføre polynomdivisjon:
$(x^3-2x^2-3x):(x-3)=x^2+x$
$$\frac{x^3-2x^2-3x}{x-3}=\frac{(x^2+x)(x-3)}{x-3}=x^2+x , \quad x\neq3 $$
Oppgave 3
a)
Jeg skriver først rekken på en annen måte:
$a+ a \cdot \frac{1}{2} + a \cdot\frac{1}{2^2} + \cdots + a \cdot\frac{1}{2^{n-1}} $
Da ser vi at dette er en geometrisk rekke, med
$a_1=a$ og $k=\frac{1}{2}$
Bruker formel for sum av de $n$ første ledda i en geometrisk rekke:
$$ S_n= a_1 \cdot \frac{k^n-1}{k-1} $$ $$ S_n= a \cdot \frac{(\frac{1}{2})^n-1}{\frac{1}{2}-1} = a \cdot \frac{\frac{1}{2^n}-1}{-\frac{1}{2}} = -2a \cdot (\frac{1}{2^n}-1) = 2a \cdot (1-\frac{1}{2^n})$$
b)
Rekka konvergerer fordi $k=\frac{1}{2}$ og dermed er $-1<k<1$. Da vet vi at en uendelig geometrisk rekke konvergerer.
Vi kan også begrunne det ut fra formelen for summen vi fant i oppg. a):
Når $n\rightarrow\infty$ vil $\frac{1}{2^n} \rightarrow 0$.
Da vil vi få:
$$ S_n = 2a \cdot (1-\frac{1}{2^n}) \rightarrow 2a \cdot (1-0) = 2a $$
c)
$ S = 2a \\ S = 10 \Rightarrow 2a=10 \\ a=\frac{10}{2}=5 $
Oppgave 4
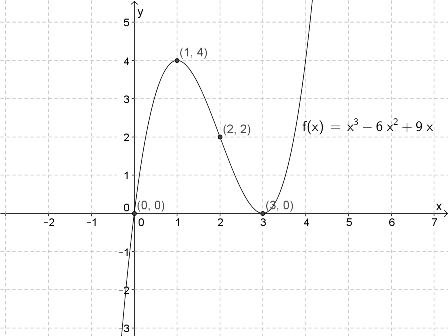
$f(x)=x^3-6x^2+9x , \quad D_f = \mathbb{R} $
a)
Nullpunktene til $f$:
$f(x)=0 \\ x^3-6x^2+9x=0 \\ x(x^2-6x+9)=0 \quad \text{faktoriserer ut} \; x\\ x(x-3)^2 = 0 \quad \text{faktoriserer vha. 2. kvadratsetning} \\ x=0 \vee x=3 $
b)
Topp-/bunnpunkter på grafen til $f$:
$f'(x)=3x^2-12x+9$
$f'(x)=0$
$3x^2-12x+9=0 \\ 3(x^2-4x+3)=0 \\ x^2-4x+3=0$
$x=\frac{-(-4)\pm \sqrt{(-4)^2-4 \cdot 3}}{2} =\frac{4 \pm \sqrt{16-12}}{2} = \frac{4 \pm \sqrt{4}}{2} = \frac{4 \pm 2}{2} \\ x=3 \vee x=1 $
$3(x^2-4x+3)=3(x-3)(x-1) $
Lager fortegnslinje:
$f(1)=4 \\ f(3)=0 $
Grafen til $f$ har et toppunkt i $(1, 4)$ og et bunnpunkt i $(3, 0)$.
c)
Vendepunktet på grafen til $f$:
$f' '(x)= 6x -12 \\ f' '(x)=0 \\ 6x-12 =0 x=2 $
Lager fortegnslinje:
$f(2)=2$
Grafen til $f$ har et vendepunkt i $(2, 2)$.
d)
Oppgave 5
a)
I punktet $A$ er $x=400$.
To av de rette linjene går også gjennom punktet $A$.
Den ene er linja $y=4,46x$ (denne har størst stigningstall, og stiger raskest av de tre rette linjene).
Den andre er linja $y=2,06x+960$ (dette er linja som tangerer grafen til $y=K(x)$ i punktet $A$).
Vi kan dermed bruke en av disse linjene, til å regne ut funksjonsverdien til $K(x)$ for $x=400$.
Vi får da:
$$E(x) = \frac{K(x)}{x} \\ E(400) = \frac{K(400)}{400} = \frac{4,46 \cdot 400}{400} = 4,46$$
b)
Grensekostnaden er $K'(x)$
Den deriverte til $K(x)$ når $x=400$, er det samme som stigningstallet til tangenten til grafen når $x=400$.
Linja $y=2,06x+960$ tangerer grafen til $K(x)$ i punktet $A$, der $x=400$.
Vi ser at denne tangenten har stigningstallet $2,06$.
$K'(400)=2,06$
c)
Den minste verdien for enhetskostnaden finner vi der enhetskostnaden er lik grensekostnaden
$$K'(x)=E(x)$$
Nå skal vi se på punket $B$. Her er $x=1000$.
Den rette linja $y=3,43x$ tangerer grafen til $K(x)$ i punktet $B$.
Vi ser at tangenten har stigningstallet $3,43$ og derfor er $K'(1000)=3,43$.
Vi kan regne ut enhetskostnaden for $x=1000$ på samme måte som vi gjorde i oppg. a). Vi bruker den rette linja til å regne ut funksjonsverdien til $K(x)$ for $x=1000$.
$$ E(1000) = \frac{K(1000)}{1000} = \frac{3,43 \cdot 1000}{1000}= 3,43 $$
Vi har nå vist at $K'(x)=E(x)$ for $x=1000$.
Den minste enhetskostnaden har vi ved produksjon av 1000 enheter, og da er enhetskostnaden 3,43 kroner per enhet.
Oppgave 6
a)
Summen av alle sannsynlighetsverdiene i en sannsynlighetsfordeling skal være lik 1.
Det gir oss første likning: $a+b+c=1$
Forventningsverdien regner vi ut slik: $\mu=E(X)=\sum x_i \cdot P(X=x_i) $ som gir:
$\mu=E(X)= (-1) \cdot a + 0 \cdot b + 1 \cdot c = -a +c $
Det gir oss andre likning: $-a+c=\frac{1}{2}$
Variansen regner vi ut slik: $Var(X)= \sum (x_i - \mu)^2 \cdot P(X=x_i) $ som gir:
$ Var(X)= (-1-\frac{1}{2})^2 \cdot a + (0-\frac{1}{2})^2 \cdot b + (1-\frac{1}{2})^2 \cdot c \\ = \frac{9}{4}a + \frac{1}{4}b + \frac{1}{4} c $
Det gir oss tredje likning: $ \frac{9}{4}a + \frac{1}{4}b + \frac{1}{4} c = \frac{7}{12} \\ 27a + 3b +3c = 7 $
b)
Jeg starter med andre likning: $-a+c=\frac{1}{2} \Rightarrow c=\frac{1}{2} +a $
Setter dette inn i første likning: $a+b+\frac{1}{2}+a=1 \\ 2a+b =\frac{1}{2} \\ b= \frac{1}{2}-2a $
Setter inn i siste likning: $27a+3(\frac{1}{2}-2a)+3(\frac{1}{2}+a)=7 \\ 27a +\frac{3}{2} - 6a + \frac{3}{2} +3a =7 \\ 24a = 4 \\ a=\frac{1}{6} $
$b=\frac{1}{2}-2 \cdot \frac{1}{6} = \frac{1}{6} \\ c=\frac{1}{2} + \frac{1}{6} = \frac{4}{6} = \frac{2}{3} $
Oppgave 7
$f(x)=x^3-3x^2+2x-2$
Den deriverte i et punkt er stigningstallet til tangenten til grafen i dette punktet.
Når vi vet at stigningtallet til tangenten er lik 2, vet vi dermed også at $f'(x)=2$.
$f'(x)=3x^2-6x+2 \\ f'(x)=2 \\ 3x^2-6x+2=2 \\ 3x^2-6x = 0 \\ 3x(x-2)=0 \\ 3x = 0 \vee x-2 = 0 \\ x=0 \vee x=2 $
$f(0)=0^3-3\cdot0^2+2\cdot 0 -2 =-2 \\ f(2)=2^3-3\cdot 2^2 +2 \cdot 2 -2 = -2 $
Punktene $(0,-2)$ og $(2, -2)$ på grafen til $f$ har tangent med stigningstall lik 2.
Del 2
Oppgave 1
a)
$p(x)=500-0,1x$
$I(x) = \mathrm{mengde} \cdot \mathrm{pris} \\ = x \cdot p(x) \\ = x \cdot (500-0,1x) \\ = 500x - 0,1x^2 $
b)
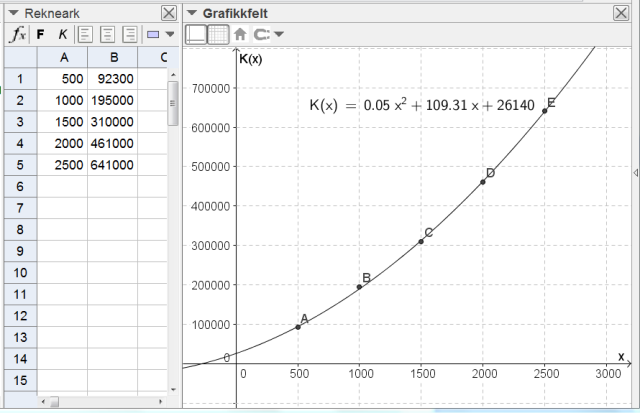
Jeg legger tabellen inn i regnearket i GeoGebra. Deretter merker jeg tallene, høyreklikker og velger "Lag liste med punkt". Når punktene blir plottet i koordinatsystemet, ser det ut som at en andregradsfunksjon kan passe bra.
Jeg bruker kommandoen "RegPoly[Liste1, 2]" og får følgende modell for kostnadsfunksjonen $K$:
$K(x) = 0,05x^2 +109,31x +26140 $
(Det står en kommentar til denne oppgaven i sensorveiledningen: "Her må det vises romslighet med hensyn til kandidatens valg av modell." F.eks. vil en lineær modell også kunne passe.)
c)
Jeg løser denne oppgaven i CAS:
Uttrykk for overskuddet blir: $O(x)=-0,15x^2+390,69x-26140$
Det største overskuddet har vi når $O'(x)=0$ Da er $x=1302,3$.
Produksjonsmengden som gir størst overskudd er 1302 enheter.
d)
Overskudd er inntekter minus kostnader.
$O(x)=I(x)-K(x)$
Overskuddet er størst når $O'(x)=0$
Vi deriverer og får: $ O'(x)=I' (x)-K' (x) $
$O' (x)=0 \\ \Updownarrow \\ I' (x)-K' (x)=0 \\ I' (x)=K'(x) $
Oppgave 2
a)
Jeg starter med arealet, og finner et uttrykk for $y$ gitt ved $x$:
$x \cdot y = 625 \\ \Rightarrow y= \frac{625}{x} $
Lengden av gjerdet består av to sider med lengde $y$, en side med lengde $x$ og et stykke med lengde $x-15$. (Steinmuren erstatter 15 m av gjerdet på den ene siden.)
Dette gir: $G(x) = x+(x-15)+2y \\ G(x)=2x+2y-15$
Setter inn for $y$: $G(x)=2x+2 \cdot (\frac{625}{x}) -15 \\ G(x)=2x+ \frac{1250}{x}-15 $
Setter på felles brøkstrek: $$G(x)=\frac{2x^2-15x+1250}{x}$$
b)
Gjerdet har kortest mulig lengde, når funksjonen $G(x)$ har et bunnpunkt.
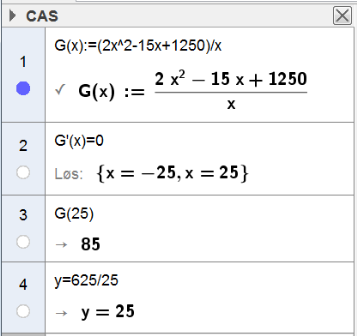
Jeg løser likningen $G'(x)=0$ i CAS:
Bare den positive løsningen kan brukes (et gjerde kan ikke ha negativ lengde).
Gjerdet har kortest mulig lengde når $x=25$. Da er er gjerdet 85 meter langt.
Fra oppg. a) vet vi at $y=\frac{625}{x}$. Det gir $y=25$.
Vi ser at $x=y$. Da er området kvadratisk.
Oppgave 3
a)
Summen av sluttverdiane blir:
$20000 \cdot 1,035 + 20000 \cdot 1,035^2+ 20000 \cdot 1,035^3+ 20000 \cdot 1,035^4$
Dette er en geometrisk rekke med 4 ledd.
$a_1 = 20000 \cdot 1,035 $ og $k=1,035$.
Jeg bruker sumformelen og regner ut vha. CAS
$S_4 = a_1 \cdot \frac{k^4-1}{k-1} $
31. desember 2010 hadde Katrine 87249 kr på sparekontoen.
b)
Dersom Katrine ikke hadde tatt ut 8000 kr hvert år, hadde hun 31. desember 2014 hatt:
$87249 \cdot 1,03^4 = 98200$ kr på kontoen.
Nå kan vi finne ut hva de 4 uttakene på 8000 kr hvert år hadde forrentet seg til dersom hun hadde spart de.
Summen av sluttverdiene blir:
$8000 \cdot 1,03 + 8000 \cdot 1,03^2 + 8000 \cdot 1,03^3 + 8000 \cdot 1,03^4 $
Dette er en geometriske rekke. $a_1=8000 \cdot 1,03 $ og $k=1,03$.
Jeg bruker sumformelen og regner ut summen vha. CAS:
31. desember 2014 har Katrine 63726 kr på sparekontoen.
Oppgave 4
a)
b)
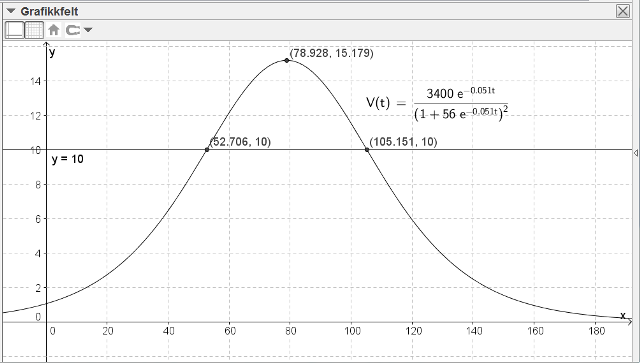
Jeg lager en linje for $y=10$. Deretter bruker jeg "skjæring mellom to objekt" til å finne skjæringspunkta mellom den rette linja og grafen til $V$.
Jeg finner skjæringspunkta $(52.7, 10)$ og $(105.2, 10)$. (Sjå figuren i oppg. a))
I følge modellen vi produksjonen være 10 milliarder fat per år 52,7 år etter 1930 og 105,2 år etter 1930. Det vil si i løpet av år 1982 og i løpet av år 2035.
c)
Jeg skriver inn i GeoGebra: "Ekstremalpunkt[V, 0, 140]" og finner toppunktet i $(78.9, 15.2)$. (Sjå figuren i oppg. a))
Produksjonen vil være størst på slutten av år 2008.
d)
Jeg bruker CAS i GeoGebra til å regne ut det bestemte integralet av $V(t)$ mellom $t=0$ og $t=85$.
Den totale produksjonen av olje fra om med 1930 til og med 2014 vil være 665,78 milliarder fat.
Oppgave 5
a)
$B_4=35$
b)
$$B_n =T_n + T_{n+3} -3 \\ B_5 = T_5 +T_8 -3 $$
$$T_n = 1 + 2 + 3 + \cdots n = \sum_1^n n$$
Jeg bruker CAS til å regne ut dette:
$B_5 = 48 $
c)
Vi kan se at $T_n=1+2+3+\cdots + n$ er summen av en aritmetisk rekke, med $a_1 =1$, $a_n=n$ og $d=1$.
Da kan vi bruke formel for sum av en aritmetisk rekke til å skrive $T_n$ på en annen måte:
$$T_n = \frac{a_1+a_n}{2} \cdot n = \frac{1+n}{2} \cdot n = \frac{(1+n)n}{2} = \frac{n^2+n}{2}$$
Vi bruker uttrykket for $T_n$ til å finne et uttrykk for $T_{n+3}$:
$$T_{n+3}= \frac{1+(n+3)}{2} \cdot (n+3) = \frac{(n+4)(n+3)}{2} = \frac{n^2+7n+12}{2} $$
Da får vi:
$$B_n = T_n + T_{n+3} -3 = \frac{n^2+n}{2} + \frac{n^2+7n+12}{2} -3 = \frac{n^2+n+n^2+7n+12-6}{2} = \frac{2n^2 +8n +6 }{2} = n^2 +4n +3$$
Oppgave 6
a)
Jeg bruker sannsynlighetskalkulatoren i GeoGebra. Jeg velger "Normalfordeling", og skriver inn "$\mu=0.33$" og "$\sigma=0.03$".
Jeg finner at $P(X>0,36)=0,1587$.
Sannsynligheten for at en tilfeldig valgt kartong inneholder mer enn 0,36 liter er 15,9 %.
b)
Jeg fortsetter med sannsynlighetskalkulatoren:
Jeg finner nå at $P(0,32<X<0,34)=0,2611$.
26,1 % av kartongene vil inneholde mellom 0,32 og 0,34 liter.
c)
Jeg setter opp hypoteser:
$H_0: \mu=0,33 \quad$ (Innholdet er riktig)
$H_1: \mu<0,33 \quad$ (Innholdet er for lite)
Vi har testet 25 tilfeldige kartonger, med $\bar{x}=0,292$ liter.
Da er samla innhold for de 25 kartongene: $25 \cdot 0,292$ liter $=7,3$ liter.
Vi går ut fra at $H_0$ gjelder. Vi lar $X_\Sigma$ være summen av innholdet til 25 tilfeldige kartonger.
Da er $X_\Sigma$ normalfordelt, med $\mu_{X_\Sigma}= n \cdot \mu = 25 \cdot 0,33= 8,25$ og $\sigma_{X_\Sigma}= \sqrt{n} \cdot \sigma = \sqrt{25} \cdot 0,03 = 0,15 $
Vi ønsker nå å finne sannsynligheten for at samla innhold til 25 kartonger er mindre enn 7,3 liter, $P(X_\Sigma < 7,3)$. Jeg bruker sannsynlighetskalkulator i GeoGebra:
P-verdien blir $P(X_\Sigma ≤ 7,3)=0 $
P-verdien er $0 \% < 5 \%$. Da kan vi forkaste nullhypotesen. Vi har grunnlag for å si at bedriften i snitt tapper for lite juice på kartongene.
d)
Vi må finne $z$ slik at $P(Z>z)=0,90$. Så kan vi bruke omregningsformelen til få finne $\mu$.
$P(Z>z)=0,90$ er det samme som at $ P(Z<z)=0,10 $.
Vi finner denne verdien i tabellen for standard normalfordeling.
$z=-1,28$ gir den verdien som er nærmest 0,10.
$$ z = \frac{x-\mu}{\sigma} \\ -1,28 = \frac{0,32-\mu}{0,03}$$
Løser likningen vha. CAS:
Forventningsverdien må være 0,36 liter for at ca. 90 % av kartongene skal inneholde mer enn 0,32 liter juice.