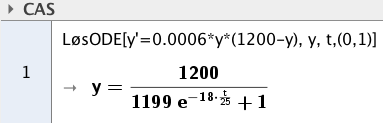R2 2016 vår LØSNING: Forskjell mellom sideversjoner
Ingen redigeringsforklaring |
|||
| (14 mellomliggende versjoner av 3 brukere er ikke vist) | |||
| Linje 1: | Linje 1: | ||
[http://www.matematikk.net/matteprat/download/file.php?id=1033 Oppgaven som pdf] | [http://www.matematikk.net/matteprat/download/file.php?id=1033 Oppgaven som pdf] | ||
[https://ndla.no/nb/node/173864?fag=98361 Løsningsforslag laget av NDLA] | |||
[https://goo.gl/GeksvX Løsningsforslag (pdf)] fra bruker joes. Send gjerne en [mailto:espen.johanssen+matematikknet@gmail.com?subject=Kommentar%20til%20R2%20V16%20fasit melding] hvis du har kommentarer til løsningsforslaget. På forhånd, takk. | [https://goo.gl/GeksvX Løsningsforslag (pdf)] fra bruker joes. Send gjerne en [mailto:espen.johanssen+matematikknet@gmail.com?subject=Kommentar%20til%20R2%20V16%20fasit melding] hvis du har kommentarer til løsningsforslaget. På forhånd, takk. | ||
| Linje 11: | Linje 13: | ||
===a=== | ===a=== | ||
$f(x)=2cos5x\quad \quad u=5x\\ f´(x) = -2sin u \cdot u´\\ f´(x)= -10 sin | $f(x)=2cos5x\quad \quad u=5x\\ f´(x) = -2sin u \cdot u´\\ f´(x)= -10 sin 5x $ | ||
===b=== | ===b=== | ||
| Linje 44: | Linje 46: | ||
==Oppgave 5== | ==Oppgave 5== | ||
===a=== | ===a===m m, | ||
===b=== | ===b=== | ||
===c=== | ===c=== | ||
==Oppgave 6== | ==Oppgave 6== | ||
$y' -xy = x \quad \quad y(0)=1$ | |||
Integrerende faktor: $e^{- \frac 12x^2}$ | |||
Vi får: | |||
$ y' \cdot e^{- \frac 12x^2} -x y \cdot e^{- \frac 12x^2} = x \cdot e^{- \frac 12x^2} \\ \int (ye^{- \frac 12x^2})' dx = \int x \cdot e^{- \frac 12x^2} dx \quad u = - \frac12 x^2, \quad du =- xdx\\ ye^{- \frac 12x^2} = - e^{- \frac 12 x^2} +C \\ y= -1 +Ce^{ \frac 12x^2} $ | |||
Bruker initialbetingenlsen og får at C = 2. | |||
Det gir: | |||
$ y = -1 + 2e^{ \frac 12 x^2}$ | |||
==Oppgave 7== | ==Oppgave 7== | ||
| Linje 74: | Linje 91: | ||
==Oppgave 4== | ==Oppgave 4== | ||
===a=== | ===a=== | ||
y er antall personer som kjenner ryktet ved tiden t. Ved t = 0 (starten) er det en person som kjenner ryktet. Ryktet sprer seg proporsjonalt med antallet som kjenner ryktet, multiplisert med antallet som ikke kjenner ryktet. | |||
Endring i antall som kjenner ryktet: | |||
$y' = 0,0006 \cdot y \cdot (1200 - y)$ | |||
===b=== | ===b=== | ||
[[File:r2-v2016-2-4b1.png]] | |||
[[File:r2-v2016-2-4b2.png]] | |||
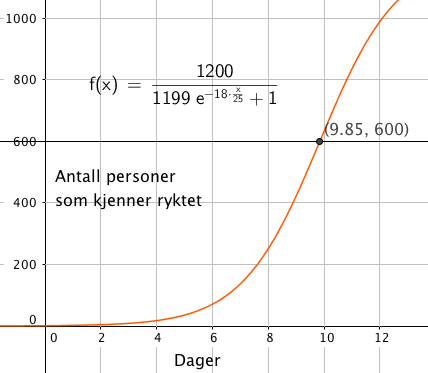
Det tar ca. 10 dager før halvparten av bygdas befolkning er kjent med ryktet. | |||
Siste sideversjon per 9. mar. 2020 kl. 18:26
Løsningsforslag (pdf) fra bruker joes. Send gjerne en melding hvis du har kommentarer til løsningsforslaget. På forhånd, takk.
Løsningsforslag (pdf) delt på eksamensfest R2 på OHG 2016-06-01
Del 1
Oppgave 1
a
$f(x)=2cos5x\quad \quad u=5x\\ f´(x) = -2sin u \cdot u´\\ f´(x)= -10 sin 5x $
b
$g(x)= e^{-2x} sin x \\ g´(x)= -2e^{-2x}sin x + e^{-2x}cos x = e^{-2x}(cos x -2sinx)$
Oppgave 2
a
$\int\limits_1^e \frac 1x dx = [3 ln x]_1^e = 3ln e - 3 ln 1 = 3-0= 3$
b
$\int \frac{2}{x^2-1} dx =\int \frac{A}{x-1} + \frac{B}{x+1} dx \\ A(x+1) +B(x-1) =2 \\ B=-1 \wedge A=1 \\ \int ( \frac{1}{x-1} - \frac{1}{x+1} ) dx = ln|x-1|- ln|x+1| + c = \frac{ln|x-1|}{ln|x+1|} +c$
Oppgave 3
a
$ f(x)=sinx \quad x \in [0, \pi ] \\ \int \limits_0^{\pi} sinxdx \\ =[- cos x ]_0^{\pi} = -cos(\pi) + cos(0) =1+1 =2 $
b
$( \frac 12 x- \frac 12 sinx \cdot cos x + c)´= \frac 12 - \frac 12(cosx \cdot cosx + sin x \cdot sin x) \\ = \frac 12 - \frac 12( (1-sin^2x) - sin^2x) \\= sin^2x$
c
$ V= \int\limits_0^{\pi}\pi sin^2xdx=\pi [\frac12x -\frac12 sinx cosx]_0^{\pi} = \pi (\frac12\pi-0-(0-0))= \frac12 \pi^2$
Oppgave 4
a
b
c
Oppgave 5
===a===m m,
b
c
Oppgave 6
$y' -xy = x \quad \quad y(0)=1$
Integrerende faktor: $e^{- \frac 12x^2}$
Vi får:
$ y' \cdot e^{- \frac 12x^2} -x y \cdot e^{- \frac 12x^2} = x \cdot e^{- \frac 12x^2} \\ \int (ye^{- \frac 12x^2})' dx = \int x \cdot e^{- \frac 12x^2} dx \quad u = - \frac12 x^2, \quad du =- xdx\\ ye^{- \frac 12x^2} = - e^{- \frac 12 x^2} +C \\ y= -1 +Ce^{ \frac 12x^2} $
Bruker initialbetingenlsen og får at C = 2.
Det gir:
$ y = -1 + 2e^{ \frac 12 x^2}$
Oppgave 7
a
b
c
d
Oppgave 8
Del 2
Oppgave 1
a
b
Oppgave 2
a
b
c
d
Oppgave 3
a
b
c
Oppgave 4
a
y er antall personer som kjenner ryktet ved tiden t. Ved t = 0 (starten) er det en person som kjenner ryktet. Ryktet sprer seg proporsjonalt med antallet som kjenner ryktet, multiplisert med antallet som ikke kjenner ryktet.
Endring i antall som kjenner ryktet:
$y' = 0,0006 \cdot y \cdot (1200 - y)$
b
Det tar ca. 10 dager før halvparten av bygdas befolkning er kjent med ryktet.