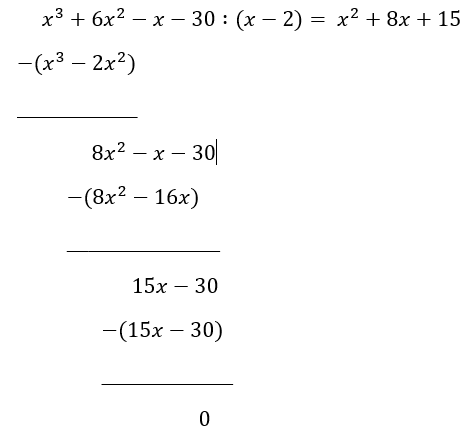R1 2018 høst LØSNING: Forskjell mellom sideversjoner
Ingen redigeringsforklaring |
|||
| (58 mellomliggende versjoner av 4 brukere er ikke vist) | |||
| Linje 1: | Linje 1: | ||
[https://www.matematikk.net/matteprat/viewtopic.php?f=13&t=48346 Diskusjon av denne oppgaven på matteprat] | [https://www.matematikk.net/matteprat/viewtopic.php?f=13&t=48346 Diskusjon av denne oppgaven på matteprat] | ||
[https://github.com/matematikk/vgs_eksamener/blob/master/l%C3%B8sningsforslag/R1/R1_18H/R1_18H_lf.pdf Løsningsforslag (pdf)] (open source, meld fra om forbedringer eller feil [https://github.com/matematikk/vgs_eksamener#hvordan-kan-jeg-bidra her]) | |||
[https://www.matematikk.net/matteprat/download/file.php?id=2285 Løsning del 1 laget av mattepratbruker mingjun] | [https://www.matematikk.net/matteprat/download/file.php?id=2285 Løsning del 1 laget av mattepratbruker mingjun] | ||
[https://matematikk.net/matteprat/download/file.php?id=2314 Løsning som PDF laget av Marius Nilsen ved Bergen Private Gymnas] | |||
[https://www.youtube.com/playlist?list=PLplkS_rtcCHWRqcA6AvAXBUnaV8OsiKjI Løsning til del 1 som videoer laget av Lektor Håkon Raustøl] | |||
=DEL 1= | |||
==Oppgave 1== | |||
===a)=== | |||
$f(x)=x^2+2x+e^x$ | |||
$f'(x)=2x+2+e^x$ | |||
===b)=== | |||
$g(x)=x^2\cdot ln \, x$ | |||
$g'(x)=2x\cdot ln \, x + x^2 \cdot \frac{1}{x} = 2x\cdot ln\, x + x$ | |||
===c)=== | |||
$h(x)=\frac{x-1}{e^{2x+1}}$ | |||
$h'(x)=\frac{1\cdot e^{2x+1}-(x-1)\cdot 2\cdot e^{2x+1}}{(e^{2x+1})^2} = \frac{1-(2x-2)}{e^{2x+1}} = \frac{-2x+1}{e^{2x+3}}$ | |||
==Oppgave 2== | |||
===a)=== | |||
$e^{2x}+7e^x-8=0$ | |||
Setter $u=e^x$ | |||
$u^2+7u-8=0 \\ (u+8)(u-1)=0 \\ u=-8 \vee u=1 \\ e^x=-8 \vee e^x=1 \\ x= 0$ | |||
Ikke mulig å ta ln(-8), forkaster derfor det ene svaret. | |||
===b)=== | |||
$ln(x^2-5x-1)-ln(3-2x)=0 \\ ln(x^2-5x-1)=ln(3-2x) \\ x^2-5x-1 = 3-2x \\ x^2-5x+2x-1-3 = 0 \\ x^2-3x-4=0 \\ (x+1)(x-4)=0 \\ x=-1 \vee x=4$ | |||
Setter inn hvert av svarene i likningen: | |||
$ln((-1)^2-5(-1)-1) - ln(3-2(-1)) = 0 \\ ln(5)-ln(5)=0$ | |||
$x=-1$ er en løsning. | |||
$ln(4^2-5\cdot 4-1)-ln(3-2\cdot 4)=0 \\ ln(-5)-ln(-5)=0$ | |||
$x=4$ er <i> ikke </i> en løsning fordi det ikke er mulig å ta ln(-5). | |||
==Oppgave 3== | |||
Vi har vektorene $\vec{a}=[2,3]$ og $\vec{b}=[-5,3]$ | |||
===a)=== | |||
$2\vec{b}-3\vec{a} = 2\cdot[-5,3]-3\cdot[2,3] = [-10,6]-[6,9] = [-16,-3]$ | |||
===b)=== | |||
$|\vec{a}|=\sqrt{2^2+3^2} = \sqrt{13}$ | |||
$|\vec{a}|<4$ fordi $\sqrt{16}=4$, og derfor er $\sqrt{13}<4$ | |||
===c)=== | |||
$\vec{a}\cdot \vec{b} = |\vec{a}|\cdot |\vec{b}|\cdot cos\,\alpha \\ cos \,\alpha = \frac{ \vec{a}\cdot \vec{b} } { |\vec{a}|\cdot |\vec{b}|} \\ cos \,\alpha = \frac{[2,3]\cdot[-5,3]}{\sqrt{13}\cdot \sqrt{(-5)^2+3^2}} \\ cos \,\alpha = \frac{-10+9}{\sqrt{13}\cdot \sqrt{34}} \\ cos \,\alpha = \frac{-1}{\sqrt{13}\cdot \sqrt{34}}$ | |||
Vi har $cos\,\alpha < 0$, hvilket betyr at vinkelen mellom de $\vec{a}$ og $\vec{b}$ er stump. | |||
==Oppgave 4== | |||
Vi har $f(x)=x^3+6x^2-x-30$ | |||
===a)=== | |||
$f(2)=2^3+6\cdot 2^2-2-30 = 8+24-2-30 = 0$ | |||
$x=2$ er et nullpunkt, så divisjonen $f(x):(x-2)$ går opp. | |||
===b)=== | |||
Utfører polynomdivisjonen: | |||
[[File: R1_H18_del1_4b.png]] | |||
Faktoriserer uttrykket: | |||
$x^3+6x^2-x-30 = (x^2+8x+15)(x-2) = (x+5)(x+3)(x-2)$ | |||
===c)=== | |||
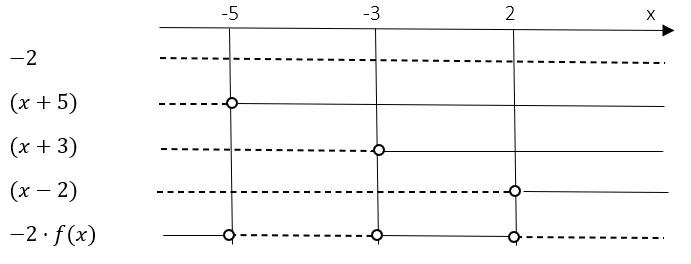
$-2\cdot f(x) \geq 0 \\ -2(x+5)(x+3)(x-2) \geq 0 $ | |||
[[File: R1_H18_del1_4c.png]] | |||
$-2\cdot f(x) \geq 0$ når $x\in \langle \leftarrow, -5] \cup [-3,2]$ | |||
==Oppgave 5== | |||
===a)=== | |||
Edelgran = E, Kvinne = K, Mann = M | |||
$P(E) = P(E|M)\cdot P(M)+P(E|K)\cdot P(K) \\ = 0,60\cdot 0,70 + 0,40\cdot 0,30 = 0,42 + 0,12 = 0,54$ | |||
Sannsynligheten for at det første treet han selger en dag, er edelgran, er 0,54. | |||
===b)=== | |||
$P(K|E) = \frac{P(K)\cdot P(E|K)}{P(E)} = \frac{0,30\cdot 0,40}{0,54} = \frac{0,12}{0,54} = \frac{12}{54} = \frac{2\cdot 6}{9\cdot 6} = \frac{2}{9}$ | |||
Sannsynligheten for at vinneren av lotteriet blir en kvinne, er $\frac{2}{9}$. | |||
==Oppgave 6== | |||
$2x^2-3x-2=x^2+x+3 \\ 2x^2-x^2-3x-x-2-3=0 \\ x^2-4x-5=0 \\ (x+1)(x-5)=0 \\ x= -1 \vee x=5 $ | |||
<i>f</i> er en kontinuerlig funksjon for $a=-1$ og $a=5$ | |||
==Oppgave 7== | |||
Vi har $g(x)=x-2ln(x^2+3) \quad , \quad x\in \R$ | |||
===a)=== | |||
$g'(x)=1- ( 0\cdot ln(x^2+3) + 2 \cdot 2x \cdot \frac{1}{x^2+3} ) \\ = 1-\frac{4x}{x^2+3} = \frac{x^2+3}{x^2+3}- \frac{4x}{x^2+3} = \frac{x^2-4x+3}{x^2+3} $ | |||
===b)=== | |||
$g'(x)=0 \\ \frac{x^2-4x+3}{x^2+3} = 0 \\ x^2-4x+3 = 0 \\ (x-1)(x-3)=0 \\ x=1 \vee x= 3$ | |||
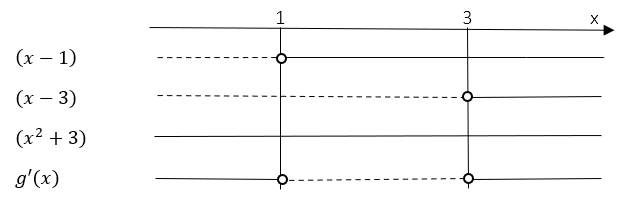
Ingen av disse x-verdiene gir null i nevner til $g'(x)$, og funksjonen <i>g(x)</i> er definert for $x\in\R$, så begge x-verdier er gyldige svar. | |||
[[File: R1_H18_del 1_7b.png]] | |||
Grafen til <i>g</i> har et toppunkt i x=1 og et bunnpunkt i x=3. | |||
===c)=== | |||
$g' '(x) = \frac{ (2x-4)(x^2+3)-(x^2-4x+3)\cdot2x }{(x^2+3)^2} = \frac{2x^3+6x-4x^2-12-(2x^3-8x^2+6x)}{(x^2+3)^2} = \frac{4x^2-12}{(x^2+3)^2} = \frac{4(x^2-3)}{(x^2+3)^2}$ | |||
$g' '(x)=0 \\ \frac{4(x^2-3)}{(x^2+3)^2} = 0 \\ x^2-3 = 0 \\ x = \pm \sqrt{3}$ | |||
Nevner i $g' '(x)$ er alltid positiv, så begge løsninger er gyldige. Vi husker at funksjonen <i>g(x)</i> er definert for $x\in\R$. | |||
Grafen til <i>g</i> har vendepunkt i $x=-\sqrt{3}$ og $x=\sqrt{3}$. | |||
==Oppgave 8== | |||
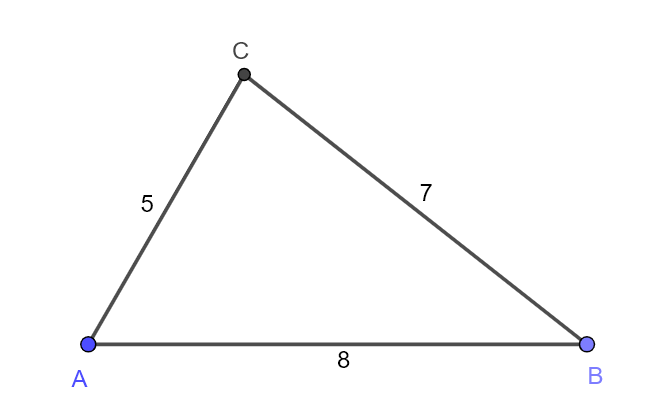
I trekanten ABC er AB = 8 cm, AC = 5 cm og BC = 7 cm. | |||
===a)=== | |||
Lager et linjestykke, lager et punkt A på linjestykket, setter passerspissen i punkt A, og slår en bue på 8 cm. Vi får punkt B i skjæringspunktet mellom linjestykke og buen. Setter passerspissen i punkt A, og slår en bue med radius 5 cm. Setter passerspissen i punkt B, og slår en bue med radius 7 cm. I skjæringspunktet mellom sirkelbuene, får vi punkt C. Lager linje AC og BC. (Dette må du gjøre for hånd). | |||
[[File: R1_H18_del1_8b.png]] | |||
===b)=== | |||
Lager halveringslinje for vinkel A og B. I skjæringspunktet mellom disse to halveringslinjene, får vi sentrum i sirkelen, punkt S. Lager normal linje gjennom punkt S på linje AB. Får punkt P i skjæringspunktet mellom AB og normalen. SP er radius i sirkelen. Setter passerspissen i punkt S og lager en sirkel med radius SP. | |||
[[File: R1_H18_del1_8b2.png]] | |||
===c)=== | |||
Konstruerer en vinkel på 60 grader i punkt A, og en i punkt C. Får da punkt E i skjæringspunktet mellom vinkelbeina. Vinkel AEC er da også 60 grader fordi vinkelsummer i en trekant er 180 grader. Setter passerspissen i punkt E og slår en sirkel med radius EA. Setter passerspissen i punkt A og slår en sirkel med radius 6 cm (siden AD = 6 cm i firkanten ABCD) . Punkt D er i skjæringspunktet mellom de to sirklene våre (se figur). Vinkel ADC er 30 grader, fordi det er en periferivinkel til sirkelen med sentrum i punkt E, som spenner over samme sirkelbue som sentralvinkelen på 60 grader. Det andre skjæringspunktet mellom de to sirklene er ikke aktuelt som punkt D, fordi vi skal ha AD < CD. | |||
[[File: R1_H18_del1_8c.png]] | |||
=DEL 2= | |||
==Oppgave 1== | |||
===a)=== | |||
Bruker sannsynlighetskalkulatoren i Geogebra, og velger binomisk sannsynlighet, med n=10 og P=0.4. | |||
[[File: R1_H18_del2_1a.png]] | |||
Sannsynligheten for at halvparten (altså fem) av plantene til Astrid får gule blomster er 0,20. | |||
===b)=== | |||
[[File: R1_H18_del2_1b.png]] | |||
Sannsynligheten for at flere enn fem av plantene til Astrid får gule blomster er 0,1662. | |||
===c)=== | |||
Bruker Microsoft Mathematics. Stian har 10 plasser hvor han kan plassere de 4 gule blomstene. Finner antall kombinasjoner av plasser for de gule blomstene. (De ledige plassene blir da fylt med røde blomster). | |||
Du kan også finne antall kombinasjoner av de 6 røde blomstene på 10 plasser, det blir det samme. | |||
[[File: R1_H18_del2_1c.png]] | |||
Stian kan plassere plantene i kassen på 210 ulike måter. | |||
==Oppgave 2== | |||
===a)=== | |||
$\angle DEA$ og $\angle DCB$ er samsvarende vinkler fordi $AE||BC$, og vinklene har et felles vinkelbein som skjærer de parallelle vinkelbeina. Samsvarende vinkler er like store, og vi har derfor $\angle DEA = \angle DCB$. | |||
===b)=== | |||
$\angle ADE$ og $\angle BDC$ er toppvinkler, og er derfor like store. I tillegg har vi de samsvarende vinklene $\angle DEA = \angle DCB$. | |||
Trekantene AED og BCD har to parvis like store vinkler, og er derfor formlike. | |||
===c)=== | |||
Vi har $\angle DCB = \angle ACD$ fordi $\angle ACB$ halveres av en vinkelhalveringslinje. Vi har allerede vist at $\angle DEA = \angle DCB$, og har følgelig $\angle ACD = \angle DEA$. Trekant AEC har altså to like store vinkler, og er derfor likebeint. | |||
===d)=== | |||
Vi har vist at trekant AEC er likebeint, så AE = AC og har lengden b. | |||
Vi har også vist at trekant AED og trekant BCD er formlike. Side AE (med lengde b) og side BC (med lengde a) er samsvarende. Side AD og side DB er også samsvarende. Forholdet mellom samsvarende sider er likt. | |||
Vi har derfor likheten $\frac{AD}{DB}=\frac{b}{a}$ | |||
===e)=== | |||
Vi har <i> a = 6, b = 7 og c = 10. </i> | |||
Vi har $AD+DB = c$ og $\frac{AD}{DB}=\frac{b}{a}$. Bruker CAS i Geogebra 6.0 og setter inn verdiene til a, b og c i disse to likhetene. Løser likningssettet i CAS. | |||
[[File: R1_H18_del2_2e.png]] | |||
$AD = \frac{70}{13}$ | |||
==Oppgave 3== | |||
Vi har punktene <i> A(3,0) og B(5,5)</i>. | |||
===a)=== | |||
Finner retningsvektor: | |||
$\vec{AB}=[5-3, 5-0]=[2,5]$ | |||
Paramaterfremstillingen blir: | |||
$ \ell: | |||
\begin{cases} | |||
x=3+2t \\ | |||
y= 5t\\ | |||
\end{cases}$ | |||
===b)=== | |||
Bruker Geogebra 6.0. Kommandoer: <i> Kurve( <Uttrykk>, <Uttrykk>, <Parametervariabel>, <Start>, <Slutt> ) </i> og <i> Linje( <Punkt>, <Retningsvektor> ) </i> | |||
[[File: R1_H18_del1_3b.png]] | |||
===c)=== | |||
$\vec{r}'(t)=[1,2t]$ angir vekstfarten til tangenten til grafen til $\vec{r}$. Stigningstallet skal være det samme som for linje $\ell$, altså $\frac{5}{2}$. | |||
$2t = \frac{5}{2} \Rightarrow t = \frac{5}{4}$ | |||
$r(\frac{5}{4})$ gir oss punktet på kurven som har samme stigningstall som linjen $\ell$. Bruker CAS i Geogebra til å finne avstanden mellom dette punktet og linjen $\ell$. Det vil være den minste avstanden mellom linjen $\ell$ og grafen til $\vec{r}$. | |||
[[File: R1_H18_del2_3c.png]] | |||
Den minste avstanden mellom linjen $\ell$ og grafen til $\vec{r}$ er $3\cdot \frac{\sqrt{29}}{8}$ | |||
==Oppgave 4== | |||
===a)=== | |||
Bruker Geogebra 6.0. | |||
[[File: R1_H18_del2_4a.png]] | |||
===b)=== | |||
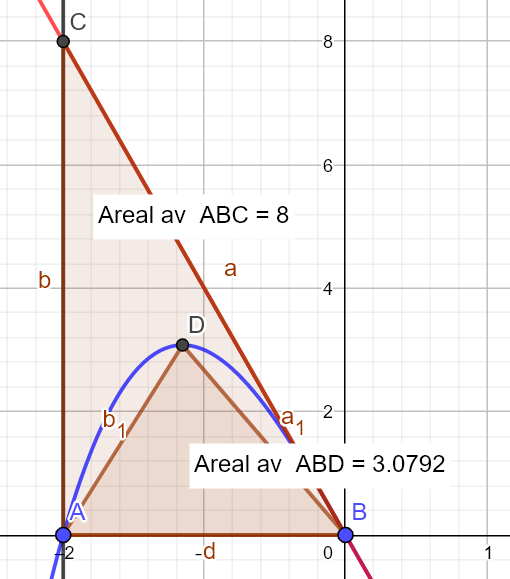
Bruker knappen <i>Mangekant</i> i Geogebra, og lager trekantene ABC og ABD. Bruker knappen <i>Areal</i> og finner arealet til trekantene ABC og ABD. | |||
[[File: R1_H18_del2_4b.png]] | |||
Forholdet mellom arealet av trekantene ABC og ABD er: | |||
$\frac{8}{3,0792}\approx 2,598 $ | |||
===c)=== | |||
[[File: R1_H18_del2_4c.png]] | |||
Definerer g(x) i linje 1. Finner nullpunktene til g i linje 2. Definerer vendetangenten s(x) i linje 3. Finner x-koordinatene til ekstremalpunktene i linje 4. | |||
Finner arealet til trekant EFG i linje 5. Formelen er $A=\frac{g\cdot h}{2}$. Grunnlinjen er avstanden mellom nullpunket x=-r og origo, altså |r|. Høyden er y-verdien til vendetangenten når $x=-r$ | |||
Finner arealet til trekant EFH i linje 6. Grunnlinjen er |r| her også. Høyden er y-verdien til funksjonen <i>g</i> i toppunktet. | |||
Finner forholdet mellom arealet av trekantene EFG og EFH i linje 7. Vi ser at forholdet er uavhengig av r. | |||
Siste sideversjon per 20. jul. 2020 kl. 19:34
Diskusjon av denne oppgaven på matteprat
Løsningsforslag (pdf) (open source, meld fra om forbedringer eller feil her)
Løsning del 1 laget av mattepratbruker mingjun
Løsning som PDF laget av Marius Nilsen ved Bergen Private Gymnas
Løsning til del 1 som videoer laget av Lektor Håkon Raustøl
DEL 1
Oppgave 1
a)
$f(x)=x^2+2x+e^x$
$f'(x)=2x+2+e^x$
b)
$g(x)=x^2\cdot ln \, x$
$g'(x)=2x\cdot ln \, x + x^2 \cdot \frac{1}{x} = 2x\cdot ln\, x + x$
c)
$h(x)=\frac{x-1}{e^{2x+1}}$
$h'(x)=\frac{1\cdot e^{2x+1}-(x-1)\cdot 2\cdot e^{2x+1}}{(e^{2x+1})^2} = \frac{1-(2x-2)}{e^{2x+1}} = \frac{-2x+1}{e^{2x+3}}$
Oppgave 2
a)
$e^{2x}+7e^x-8=0$
Setter $u=e^x$
$u^2+7u-8=0 \\ (u+8)(u-1)=0 \\ u=-8 \vee u=1 \\ e^x=-8 \vee e^x=1 \\ x= 0$
Ikke mulig å ta ln(-8), forkaster derfor det ene svaret.
b)
$ln(x^2-5x-1)-ln(3-2x)=0 \\ ln(x^2-5x-1)=ln(3-2x) \\ x^2-5x-1 = 3-2x \\ x^2-5x+2x-1-3 = 0 \\ x^2-3x-4=0 \\ (x+1)(x-4)=0 \\ x=-1 \vee x=4$
Setter inn hvert av svarene i likningen:
$ln((-1)^2-5(-1)-1) - ln(3-2(-1)) = 0 \\ ln(5)-ln(5)=0$
$x=-1$ er en løsning.
$ln(4^2-5\cdot 4-1)-ln(3-2\cdot 4)=0 \\ ln(-5)-ln(-5)=0$
$x=4$ er ikke en løsning fordi det ikke er mulig å ta ln(-5).
Oppgave 3
Vi har vektorene $\vec{a}=[2,3]$ og $\vec{b}=[-5,3]$
a)
$2\vec{b}-3\vec{a} = 2\cdot[-5,3]-3\cdot[2,3] = [-10,6]-[6,9] = [-16,-3]$
b)
$|\vec{a}|=\sqrt{2^2+3^2} = \sqrt{13}$
$|\vec{a}|<4$ fordi $\sqrt{16}=4$, og derfor er $\sqrt{13}<4$
c)
$\vec{a}\cdot \vec{b} = |\vec{a}|\cdot |\vec{b}|\cdot cos\,\alpha \\ cos \,\alpha = \frac{ \vec{a}\cdot \vec{b} } { |\vec{a}|\cdot |\vec{b}|} \\ cos \,\alpha = \frac{[2,3]\cdot[-5,3]}{\sqrt{13}\cdot \sqrt{(-5)^2+3^2}} \\ cos \,\alpha = \frac{-10+9}{\sqrt{13}\cdot \sqrt{34}} \\ cos \,\alpha = \frac{-1}{\sqrt{13}\cdot \sqrt{34}}$
Vi har $cos\,\alpha < 0$, hvilket betyr at vinkelen mellom de $\vec{a}$ og $\vec{b}$ er stump.
Oppgave 4
Vi har $f(x)=x^3+6x^2-x-30$
a)
$f(2)=2^3+6\cdot 2^2-2-30 = 8+24-2-30 = 0$
$x=2$ er et nullpunkt, så divisjonen $f(x):(x-2)$ går opp.
b)
Utfører polynomdivisjonen:
Faktoriserer uttrykket:
$x^3+6x^2-x-30 = (x^2+8x+15)(x-2) = (x+5)(x+3)(x-2)$
c)
$-2\cdot f(x) \geq 0 \\ -2(x+5)(x+3)(x-2) \geq 0 $
$-2\cdot f(x) \geq 0$ når $x\in \langle \leftarrow, -5] \cup [-3,2]$
Oppgave 5
a)
Edelgran = E, Kvinne = K, Mann = M
$P(E) = P(E|M)\cdot P(M)+P(E|K)\cdot P(K) \\ = 0,60\cdot 0,70 + 0,40\cdot 0,30 = 0,42 + 0,12 = 0,54$
Sannsynligheten for at det første treet han selger en dag, er edelgran, er 0,54.
b)
$P(K|E) = \frac{P(K)\cdot P(E|K)}{P(E)} = \frac{0,30\cdot 0,40}{0,54} = \frac{0,12}{0,54} = \frac{12}{54} = \frac{2\cdot 6}{9\cdot 6} = \frac{2}{9}$
Sannsynligheten for at vinneren av lotteriet blir en kvinne, er $\frac{2}{9}$.
Oppgave 6
$2x^2-3x-2=x^2+x+3 \\ 2x^2-x^2-3x-x-2-3=0 \\ x^2-4x-5=0 \\ (x+1)(x-5)=0 \\ x= -1 \vee x=5 $
f er en kontinuerlig funksjon for $a=-1$ og $a=5$
Oppgave 7
Vi har $g(x)=x-2ln(x^2+3) \quad , \quad x\in \R$
a)
$g'(x)=1- ( 0\cdot ln(x^2+3) + 2 \cdot 2x \cdot \frac{1}{x^2+3} ) \\ = 1-\frac{4x}{x^2+3} = \frac{x^2+3}{x^2+3}- \frac{4x}{x^2+3} = \frac{x^2-4x+3}{x^2+3} $
b)
$g'(x)=0 \\ \frac{x^2-4x+3}{x^2+3} = 0 \\ x^2-4x+3 = 0 \\ (x-1)(x-3)=0 \\ x=1 \vee x= 3$
Ingen av disse x-verdiene gir null i nevner til $g'(x)$, og funksjonen g(x) er definert for $x\in\R$, så begge x-verdier er gyldige svar.
Grafen til g har et toppunkt i x=1 og et bunnpunkt i x=3.
c)
$g' '(x) = \frac{ (2x-4)(x^2+3)-(x^2-4x+3)\cdot2x }{(x^2+3)^2} = \frac{2x^3+6x-4x^2-12-(2x^3-8x^2+6x)}{(x^2+3)^2} = \frac{4x^2-12}{(x^2+3)^2} = \frac{4(x^2-3)}{(x^2+3)^2}$
$g' '(x)=0 \\ \frac{4(x^2-3)}{(x^2+3)^2} = 0 \\ x^2-3 = 0 \\ x = \pm \sqrt{3}$
Nevner i $g' '(x)$ er alltid positiv, så begge løsninger er gyldige. Vi husker at funksjonen g(x) er definert for $x\in\R$.
Grafen til g har vendepunkt i $x=-\sqrt{3}$ og $x=\sqrt{3}$.
Oppgave 8
I trekanten ABC er AB = 8 cm, AC = 5 cm og BC = 7 cm.
a)
Lager et linjestykke, lager et punkt A på linjestykket, setter passerspissen i punkt A, og slår en bue på 8 cm. Vi får punkt B i skjæringspunktet mellom linjestykke og buen. Setter passerspissen i punkt A, og slår en bue med radius 5 cm. Setter passerspissen i punkt B, og slår en bue med radius 7 cm. I skjæringspunktet mellom sirkelbuene, får vi punkt C. Lager linje AC og BC. (Dette må du gjøre for hånd).
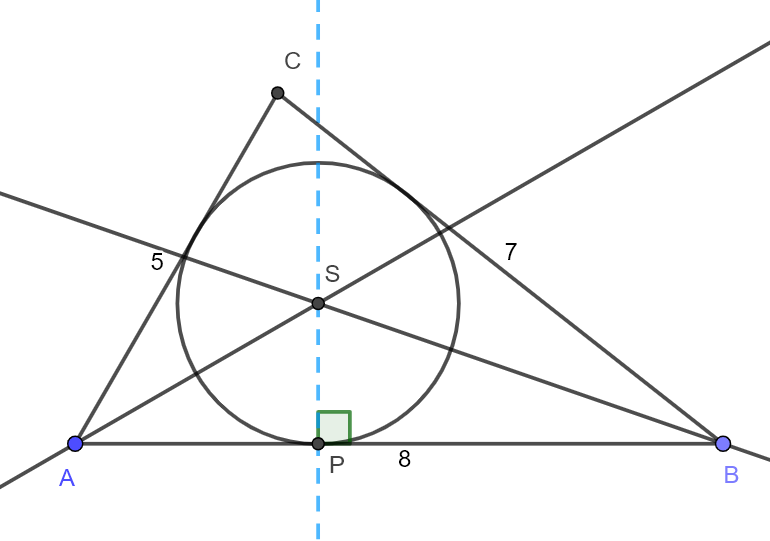
b)
Lager halveringslinje for vinkel A og B. I skjæringspunktet mellom disse to halveringslinjene, får vi sentrum i sirkelen, punkt S. Lager normal linje gjennom punkt S på linje AB. Får punkt P i skjæringspunktet mellom AB og normalen. SP er radius i sirkelen. Setter passerspissen i punkt S og lager en sirkel med radius SP.
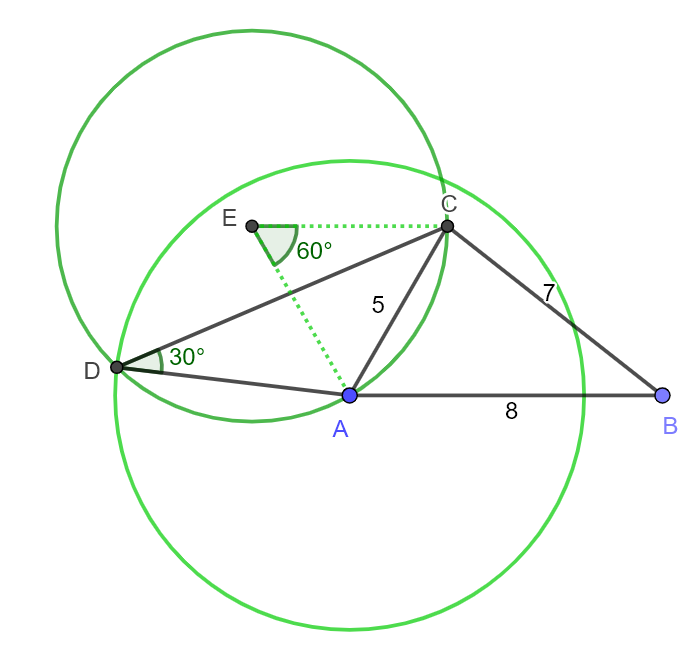
c)
Konstruerer en vinkel på 60 grader i punkt A, og en i punkt C. Får da punkt E i skjæringspunktet mellom vinkelbeina. Vinkel AEC er da også 60 grader fordi vinkelsummer i en trekant er 180 grader. Setter passerspissen i punkt E og slår en sirkel med radius EA. Setter passerspissen i punkt A og slår en sirkel med radius 6 cm (siden AD = 6 cm i firkanten ABCD) . Punkt D er i skjæringspunktet mellom de to sirklene våre (se figur). Vinkel ADC er 30 grader, fordi det er en periferivinkel til sirkelen med sentrum i punkt E, som spenner over samme sirkelbue som sentralvinkelen på 60 grader. Det andre skjæringspunktet mellom de to sirklene er ikke aktuelt som punkt D, fordi vi skal ha AD < CD.
DEL 2
Oppgave 1
a)
Bruker sannsynlighetskalkulatoren i Geogebra, og velger binomisk sannsynlighet, med n=10 og P=0.4.
Sannsynligheten for at halvparten (altså fem) av plantene til Astrid får gule blomster er 0,20.
b)
Sannsynligheten for at flere enn fem av plantene til Astrid får gule blomster er 0,1662.
c)
Bruker Microsoft Mathematics. Stian har 10 plasser hvor han kan plassere de 4 gule blomstene. Finner antall kombinasjoner av plasser for de gule blomstene. (De ledige plassene blir da fylt med røde blomster). Du kan også finne antall kombinasjoner av de 6 røde blomstene på 10 plasser, det blir det samme.
Stian kan plassere plantene i kassen på 210 ulike måter.
Oppgave 2
a)
$\angle DEA$ og $\angle DCB$ er samsvarende vinkler fordi $AE||BC$, og vinklene har et felles vinkelbein som skjærer de parallelle vinkelbeina. Samsvarende vinkler er like store, og vi har derfor $\angle DEA = \angle DCB$.
b)
$\angle ADE$ og $\angle BDC$ er toppvinkler, og er derfor like store. I tillegg har vi de samsvarende vinklene $\angle DEA = \angle DCB$.
Trekantene AED og BCD har to parvis like store vinkler, og er derfor formlike.
c)
Vi har $\angle DCB = \angle ACD$ fordi $\angle ACB$ halveres av en vinkelhalveringslinje. Vi har allerede vist at $\angle DEA = \angle DCB$, og har følgelig $\angle ACD = \angle DEA$. Trekant AEC har altså to like store vinkler, og er derfor likebeint.
d)
Vi har vist at trekant AEC er likebeint, så AE = AC og har lengden b.
Vi har også vist at trekant AED og trekant BCD er formlike. Side AE (med lengde b) og side BC (med lengde a) er samsvarende. Side AD og side DB er også samsvarende. Forholdet mellom samsvarende sider er likt.
Vi har derfor likheten $\frac{AD}{DB}=\frac{b}{a}$
e)
Vi har a = 6, b = 7 og c = 10.
Vi har $AD+DB = c$ og $\frac{AD}{DB}=\frac{b}{a}$. Bruker CAS i Geogebra 6.0 og setter inn verdiene til a, b og c i disse to likhetene. Løser likningssettet i CAS.
$AD = \frac{70}{13}$
Oppgave 3
Vi har punktene A(3,0) og B(5,5).
a)
Finner retningsvektor:
$\vec{AB}=[5-3, 5-0]=[2,5]$
Paramaterfremstillingen blir:
$ \ell: \begin{cases} x=3+2t \\ y= 5t\\ \end{cases}$
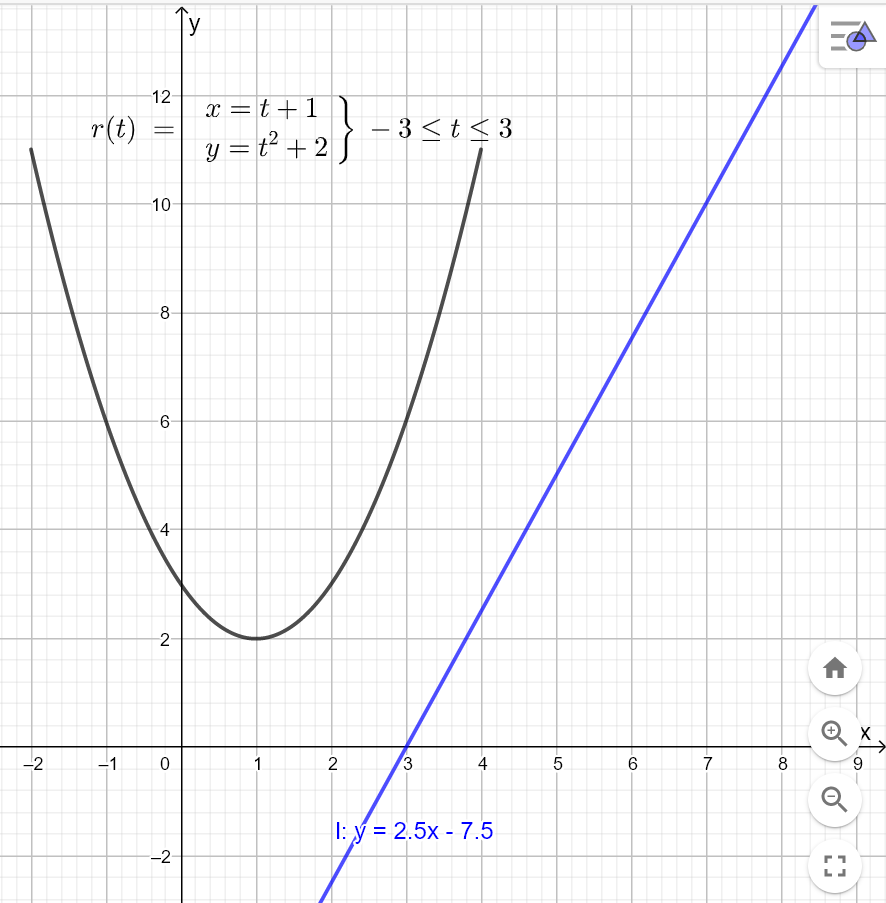
b)
Bruker Geogebra 6.0. Kommandoer: Kurve( <Uttrykk>, <Uttrykk>, <Parametervariabel>, <Start>, <Slutt> ) og Linje( <Punkt>, <Retningsvektor> )
c)
$\vec{r}'(t)=[1,2t]$ angir vekstfarten til tangenten til grafen til $\vec{r}$. Stigningstallet skal være det samme som for linje $\ell$, altså $\frac{5}{2}$.
$2t = \frac{5}{2} \Rightarrow t = \frac{5}{4}$
$r(\frac{5}{4})$ gir oss punktet på kurven som har samme stigningstall som linjen $\ell$. Bruker CAS i Geogebra til å finne avstanden mellom dette punktet og linjen $\ell$. Det vil være den minste avstanden mellom linjen $\ell$ og grafen til $\vec{r}$.
Den minste avstanden mellom linjen $\ell$ og grafen til $\vec{r}$ er $3\cdot \frac{\sqrt{29}}{8}$
Oppgave 4
a)
Bruker Geogebra 6.0.
b)
Bruker knappen Mangekant i Geogebra, og lager trekantene ABC og ABD. Bruker knappen Areal og finner arealet til trekantene ABC og ABD.
Forholdet mellom arealet av trekantene ABC og ABD er:
$\frac{8}{3,0792}\approx 2,598 $
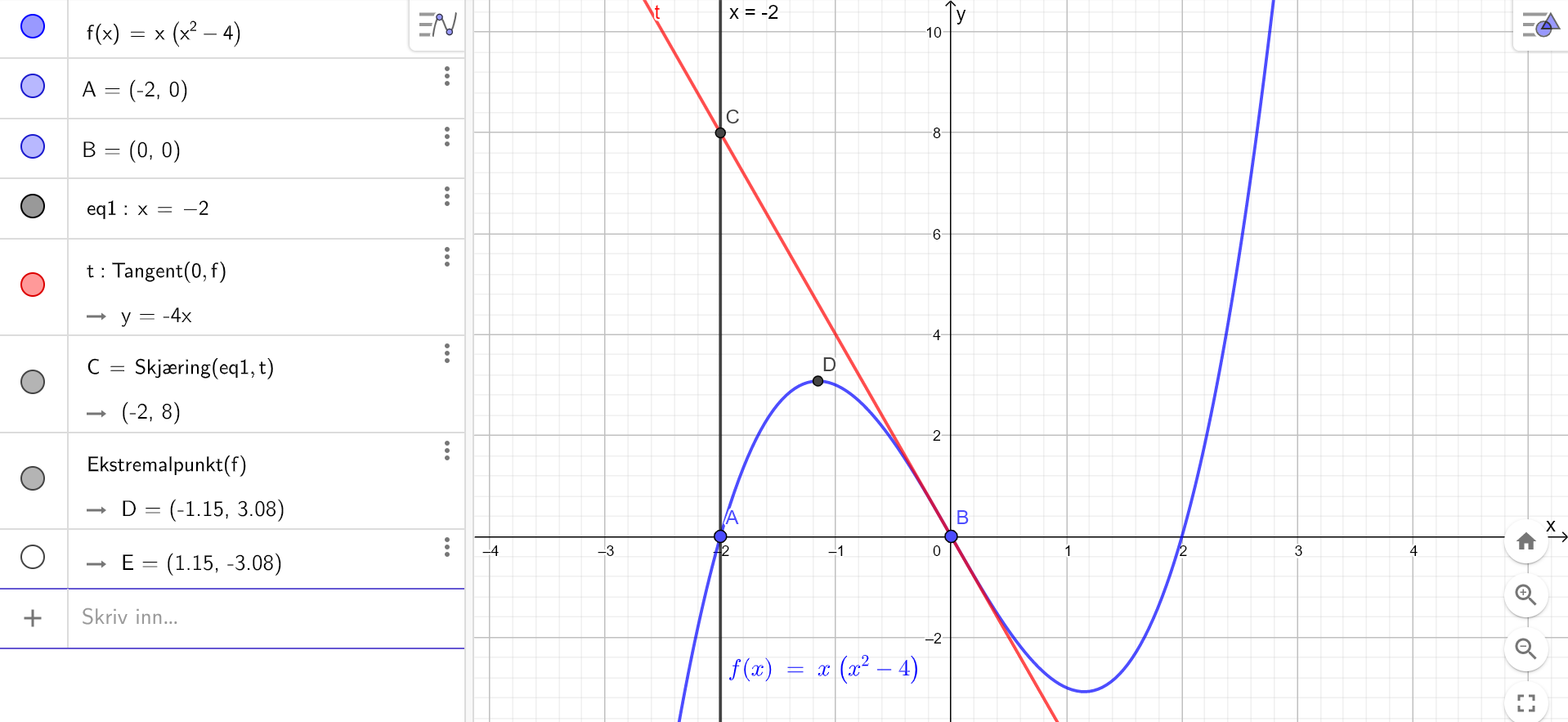
c)
Definerer g(x) i linje 1. Finner nullpunktene til g i linje 2. Definerer vendetangenten s(x) i linje 3. Finner x-koordinatene til ekstremalpunktene i linje 4.
Finner arealet til trekant EFG i linje 5. Formelen er $A=\frac{g\cdot h}{2}$. Grunnlinjen er avstanden mellom nullpunket x=-r og origo, altså |r|. Høyden er y-verdien til vendetangenten når $x=-r$
Finner arealet til trekant EFH i linje 6. Grunnlinjen er |r| her også. Høyden er y-verdien til funksjonen g i toppunktet.
Finner forholdet mellom arealet av trekantene EFG og EFH i linje 7. Vi ser at forholdet er uavhengig av r.