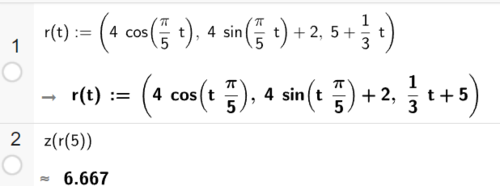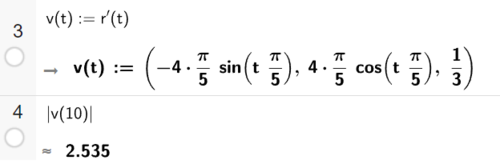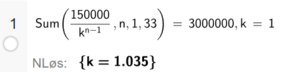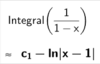R2 2025 vår LØSNING: Forskjell mellom sideversjoner
| (42 mellomliggende sideversjoner av samme bruker vises ikke) | |||
| Linje 80: | Linje 80: | ||
===c)=== | ===c)=== | ||
Induksjonsgrunnlag; vi sjekker at formelen stemmer for n=1: | |||
$a_1=\frac{1(1+3)}{2}=2$ | |||
Formelen stemmer for n=1. | |||
Induksjonstrinnet; vi antar at formelen gjelder for $n= k$: | |||
$a_k = \frac{k(k+3)}{2}=\frac{k^2+3k}{2}$ | |||
Finner $a_{k+1}$ ved å bruke den rekursive formelen fra programmet i oppgave a): | |||
$a_{k+1}=a_k+k+2= \frac{k^2+3k}{2}+k+2 = \frac{k^2+3k}{2}+\frac{2k}{2}+\frac{4}{2}= \frac{k^2+5k+4}{2}$ | |||
Sjekker om formelen stemmer for $k+1$: | |||
$a_{k+1}=\frac{(k+1)((k+1)+3)}{2}=\frac{(k+1)(k+4)}{2}=\frac{k^2+5k+4}{2}$ | |||
Konklusjon: dersom formelen stemmer for $n = k$, må den også stemme for $n = k + 1$. Vi har vist at formelen stemmer $n = 1$, og derfor må den også stemme for $n = 2, n = 3...$ Vi har vist at formelen stemmer for alle $n\geq 1$. | |||
==Oppgave 4== | ==Oppgave 4== | ||
Funksjonen f er gitt ved: | |||
$f(x)=2\cdot \sqrt{3} \cdot sin(2x+\frac{\pi}{6}), \quad D_f=\langle 0,\frac{\pi}{2}\rangle$ | |||
Generelt er sinusfunksjoner gitt ved: | |||
$f(x)=Asin(kx+\phi)+d$ | |||
===a)=== | |||
Amplitude: $A=2\sqrt{3}$ | |||
Likevekstlinje: $d=0$ | |||
Periode: $p=\frac{2\pi}{k}=\frac{2\pi}{2}=\pi$ | |||
Faseforskyvning: $x_f=-\frac{\phi}{k}=-\frac{\frac{\pi}{6}}{2}=-\frac{\pi}{12}$ | |||
===b)=== | |||
$f(x)=\sqrt{3}$ | |||
$2\cdot \sqrt{3} \cdot sin(2x+\frac{\pi}{6})=\sqrt{3}$ | |||
$sin(2x+\frac{\pi}{6})=\frac{1}{2}$ | |||
$2x+\frac{\pi}{6}=sin^{-1}(\frac{1}{2})$ | |||
$2x+\frac{\pi}{6}=\frac{\pi}{6}+k\cdot 2\pi \quad \vee \quad 2x+\frac{\pi}{6}=\frac{5\pi}{6}+k\cdot 2\pi $ | |||
$x=k\pi \quad \vee \quad x=\frac{\pi}{3}+k\pi$ | |||
Den første løsningen er ikke i funksjonens definisjonområde og forkastes derfor. Den andre løsningen er gyldig for k=1: | |||
$x=\frac{\pi}{3}$ | |||
===c)=== | |||
Funksjonen g er gitt ved: | |||
$g(x)=3sin(2x)+\sqrt{3} cos(2x),\quad D_g=\langle0,2\pi\rangle$ | |||
Vi skal løse likningen $g(x)=\sqrt{3}$ | |||
Vi kan omforme likningen til en sinusfunksjon. Generelt har vi sammenhengen: | |||
$a\,sin(kx)+ b\,cos(kx)=A\,sin(kx+\phi)$ | |||
hvor | |||
$A=\sqrt{a^2+b^2}$ | |||
og | |||
$tan\, \phi = \frac{b}{a}$ | |||
For g(x) har vi: | |||
$A=\sqrt{3^2+\sqrt{3}^2}=\sqrt{12}=2\sqrt{3}$ | |||
$tan\,\phi=\frac{\sqrt{3}}{3}\quad \Rightarrow \quad \phi=\frac{\pi}{6}$ | |||
Da er $g(x)=2\cdot \sqrt{3} \cdot sin(2x+\frac{\pi}{6})=f(x)$ | |||
For likningen $g(x)=\sqrt{3}$, kan vi bruke løsningen fra oppgave b) i definisjonsområdet $D_g=\langle0,2\pi\rangle$ | |||
$x=k\pi \quad \vee \quad x=\frac{\pi}{3}+k\pi$ | |||
Den første løsningen er gyldig for k= 1, og den andre løsningen er gyldig for k=0 og k=1. Vi har: | |||
$x=\frac{\pi}{3} \quad \vee \quad x=\pi \quad \vee \quad x=\frac{4\pi}{3}$ | |||
==Oppgave 5== | ==Oppgave 5== | ||
===a)=== | |||
$\vec{AB}=[2,3,0]$ | |||
$\vec{AC}=[1,4,1]$ | |||
$\vec{BA}=[-2,-3,0]$ | |||
$\vec{BC}=[-1,1,1]$ | |||
$\vec{CB}=[1,-1,-1]$ | |||
$\vec{CA}=[-1,-4,-1]$ | |||
$\vec{AB}\cdot \vec{AC}=2+12+1=15 \quad \Rightarrow \quad \angle A < 90^o$ | |||
$\vec{BA}\cdot \vec{BC}=2-3+0=-1 \quad \Rightarrow \quad \angle B > 90^o$ | |||
$\vec{CA}\cdot \vec{CB}=-1+4+1=4 \quad \Rightarrow \quad \angle C < 90^o$ | |||
Vinkel B er større enn 90 grader, fordi skalarproduktet til vinkelbeina er negativt (indikerer at cosinus til vinkelen er negativ, og vinkelen derfor er større enn 90 grader). | |||
===b)=== | |||
Arealet av trekanten er halvparten av arealet utspent av to av sidene (to av vektorene). | |||
$\vec{BA}\times\vec{BC} = \left| \begin{array}{ccc}i & j & k \\-2 & -3 & 0 \\-1 & 1 & 1 \end{array} \right | = [-3+0,0-(-2), -2-3] = [-3,2,-5]$ | |||
$A_{ABC}= \frac{1}{2} |[-3,2,-5]| = \frac{1}{2}\sqrt{(-3)^2+2^2+(-5)^2}=\frac{1}{2}\sqrt{9+4+25}=\frac{1}{2}\sqrt{38}$ | |||
===c)=== | |||
$\vec{DE}=[-1,-4,-1]$ | |||
Vi har en normalvektor til planet som trekant ABC ligger på, fra oppgave b): $ [-3,2,-5] $ | |||
Sjekker om normalvektoren til planet og linja står vinkelrett på hverandre, ved å sjekke om skalarproduktet blir 0: | |||
$[-1,-4,-1]\cdot [-3,2,-5]=3-8+5=0$ | |||
Normalvektoren til planet og linja står vinkelrett på hverandre, som vil si at planet og linja er parallelle. Grenen vil aldri treffe bordplata. | |||
==Oppgave 6== | ==Oppgave 6== | ||
Programmet summerer arealet av små rektangler med bredde dx og lengde f(x), pluss små rektangler med bredde dx og lengde g(x). Dette gjør programmet fra x = 0 til x = 2, med intervaller på 0.0001. Alle arealene summeres. Dette er det samme som summen av integralene til begge funksjonene fra x=0 til x=2. | |||
$\int_0^2 f(x) dx = \int_0^2 x^3 dx = [\frac{1}{4}x^4]_0^2=(\frac{1}{4}\cdot 2^4)-(\frac{1}{4}\cdot 0^4)=\frac{1}{4}\cdot 16-0=4$ | |||
$\int_0^2 g(x) dx = \int_0^2 -2x^2 dx = [-\frac{2}{3}x^3]_0^2=(-\frac{2}{3}\cdot 2^3)-(-\frac{2}{3}\cdot 0^3)=-\frac{2}{3}\cdot 8-0=-\frac{16}{3}$ | |||
Summerer arealene: | |||
$4+(-\frac{16}{3})=\frac{12}{3}-\frac{16}{3}=-\frac{4}{3}$ | |||
Programmet skriver ut $-\frac{4}{3}$, eller $-1,33333...$ | |||
==Oppgave 7== | ==Oppgave 7== | ||
===a)=== | |||
Buelengden L til en sirkelsektor er gitt ved: $L=2\pi r \cdot \frac{v}{360^o}$, hvor r er radiusen og v er vinkelen av sektoren. | |||
Vi har: | |||
$4=2\pi \cdot 3 \cdot \frac{v}{360^o}$ | |||
$v = \frac{4\cdot 360^o}{6\pi}$ | |||
$v = \frac{240^o}{\pi}$ | |||
Hvis vi runder av pi til ca. 3, vet vi at vinkelen er mindre enn 80 grader. | |||
For radianer har vi at $L=r\cdot v$ | |||
Vi har: | |||
$4=3\cdot v$ | |||
$v=\frac{4}{3}\approx 1,333...$ | |||
===b)=== | |||
$tan\,u=2$ | |||
$\frac{sin\,u}{cos\,u}=2$ | |||
$sin\,u=2cos\,u$ | |||
Setter inn verdien for sin u i enhetsformelen: | |||
$sin^2 u + cos^2 u = 1$ | |||
$(2 cos\,u)^2 + cos^2 u=1$ | |||
$5 cos^2 u = 1$ | |||
$cos\,u = \pm\sqrt{\frac{1}{5}}=\pm\frac{\sqrt{5}}{5}$ | |||
$sin\, u = 2 cos\,u = \pm \frac{2\sqrt{5}}{5}$ | |||
Siden $u\in\langle0,\frac{\pi}{2}\rangle$, har vi $sin\,u=\frac{2\sqrt{5}}{5}$ og $cos\,u=\frac{\sqrt{5}}{5}$ | |||
=DEL 2= | =DEL 2= | ||
==Oppgave 1== | ==Oppgave 1== | ||
===a)=== | |||
Bruker CAS i Geogebra. | |||
[[File: R2_V25_del2_1a.png|500px]] | |||
Bilen er ca. 6,67 meter over bakkenivå etter 5 sekunder. | |||
===b)=== | |||
Fartsvektoren er definert på linje 3. | |||
[[File: R2_V25_del2_1b.png|500px]] | |||
Farten til bilen etter 10 sekunder er ca. 2,5 meter per sekund. | |||
===c)=== | |||
Generelt er sinusfunksjoner gitt ved: | |||
$f(x)=Asin(kx+\phi)+d$ | |||
For $\vec{r}(t)$ er $k=\frac{\pi}{5}$ | |||
Periode: $p=\frac{2\pi}{k}=\frac{2\pi}{\frac{\pi}{5}}=10$ | |||
En periode er på 10 sekunder. Finner høyden etter 10 sekunder, minus høyden ved start. | |||
[[File: R2_V25_del2_1c.png|250px]] | |||
Høyden mellom etasjene kan være ca. 3,33 meter. | |||
==Oppgave 2== | ==Oppgave 2== | ||
| Linje 115: | Linje 337: | ||
Bruker at summen av nåverdiene til terminbeløpet, skal bli lik lånebeløpet: | Bruker at summen av nåverdiene til terminbeløpet, skal bli lik lånebeløpet: | ||
[[File: | [[File: S2_V25_del2_4b2.png|300px]] | ||
Nora har regnet med at den årlige rentesatsen på lånet er | Nora har regnet med at den årlige rentesatsen på lånet er 3,5 %. | ||
==Oppgave 3== | ==Oppgave 3== | ||
===a)=== | |||
Bruker CAS i Geogebra. | |||
[[File: R2_V25_del2_3a.png|350px]] | |||
Det tar 0,97 sekunder før akselerasjonen til haren er null. Det forteller at haren har nådd toppfarten sin etter 0,97 sekunder (toppunkt på grafen til v). | |||
===b)=== | |||
[[File: R2_V25_del2_3b.png|300px]] | |||
Haren løper 103,4 meter i løpet av de første 7 sekundene. | |||
===c)=== | |||
[[File: R2_V25_del2_3c.png|600px]] | |||
Definerer funksjonen for gjennomsnittsfarten i linje 4. Finner ut hvor mange sekunder det tar for haren å løpe 200 meter i linje 5. Finner gjennomsnittsfarten etter 14,954 sekunder (200 meter) i linje 5. | |||
Gjennomsnittsfarten til haren er 13,37 meter per sekund de første 200 meterne. | |||
==Oppgave 4== | ==Oppgave 4== | ||
Siste sideversjon per 3. aug. 2025 kl. 17:19
Diskusjon av oppgaven på matteprat
Løsningsforslag laget av Lektor Seland
Løsningsforslag som video laget av UDL.no
DEL 1
Oppgave 1
a)
$\int_0^1 (2e^x +2x^2)dx $
$=[2e^x+\frac{2}{3}x^3]_0^1$
$=(2e+\frac{2}{3})-2$
$=2e-\frac{4}{3}$
b)
$\int\frac{2x-1}{x^2-x-6}dx$
Bruker integrasjon ved variabelskifte:
$u=x^2-x-6$
$u'=2x-1$
$u'=\frac{du}{dx} \Rightarrow dx = \frac{du}{u'}$
$\int\frac{2x-1}{x^2-x-6}dx = \int\frac{u'}{u}dx=\int\frac{u'}{u}\frac{du}{u'} = \int \frac{1}{u}du = ln |u|+C = ln |x^2-x-6|+C$
Det er også mulig å bruke integrasjon ved delbrøkoppspalting.
Oppgave 2
Vi har at
- $f'(x)=-\frac{2}{x^3}$
- $\int_{1}^{2}f(x)dx=\frac{11}{14}$
Integrerer f'(x) for å få et uttrykk for f(x):
$f(x)=\int -\frac{2}{x^3} dx = -2\int x^{-3}dx=\frac{-2}{-2}x^{-2} +C=\frac{1}{x^2}+C$
Bruker det bestemte integralet som likning for å finne C:
$\int_{1}^{2}(\frac{1}{x^2}+C )\, dx=\frac{11}{14}$
$[-\frac{1}{x}+Cx]_{1}^{2}=\frac{11}{14}$
$-\frac{1}{2}+2C-(-1+C)=\frac{11}{14}$
$C+\frac{1}{2}=\frac{11}{14}$
$C=\frac{11}{14}-\frac{7}{14}$
$C=\frac{4}{14}=\frac{2}{7}$
Vi har:
$f(x)=\frac{1}{x^2}+\frac{2}{7}$
Oppgave 3
a)
Rekken starter med tallet 2. For å finne neste tall, tar man forrige tall pluss forrige tall sitt figurnummer pluss 2. Vi har $a_{n+1} = a_n+n+2 $
Når koden kjøres, skrives de 5 første tallene i rekken ut, nemlig 2, 5, 9, 14, 20.
b)
Eleven ønsker å finne summen av de 5 første tallene i rekken. Resultatet som skrives ut blir 50.
c)
Induksjonsgrunnlag; vi sjekker at formelen stemmer for n=1:
$a_1=\frac{1(1+3)}{2}=2$
Formelen stemmer for n=1.
Induksjonstrinnet; vi antar at formelen gjelder for $n= k$:
$a_k = \frac{k(k+3)}{2}=\frac{k^2+3k}{2}$
Finner $a_{k+1}$ ved å bruke den rekursive formelen fra programmet i oppgave a):
$a_{k+1}=a_k+k+2= \frac{k^2+3k}{2}+k+2 = \frac{k^2+3k}{2}+\frac{2k}{2}+\frac{4}{2}= \frac{k^2+5k+4}{2}$
Sjekker om formelen stemmer for $k+1$:
$a_{k+1}=\frac{(k+1)((k+1)+3)}{2}=\frac{(k+1)(k+4)}{2}=\frac{k^2+5k+4}{2}$
Konklusjon: dersom formelen stemmer for $n = k$, må den også stemme for $n = k + 1$. Vi har vist at formelen stemmer $n = 1$, og derfor må den også stemme for $n = 2, n = 3...$ Vi har vist at formelen stemmer for alle $n\geq 1$.
Oppgave 4
Funksjonen f er gitt ved:
$f(x)=2\cdot \sqrt{3} \cdot sin(2x+\frac{\pi}{6}), \quad D_f=\langle 0,\frac{\pi}{2}\rangle$
Generelt er sinusfunksjoner gitt ved:
$f(x)=Asin(kx+\phi)+d$
a)
Amplitude: $A=2\sqrt{3}$
Likevekstlinje: $d=0$
Periode: $p=\frac{2\pi}{k}=\frac{2\pi}{2}=\pi$
Faseforskyvning: $x_f=-\frac{\phi}{k}=-\frac{\frac{\pi}{6}}{2}=-\frac{\pi}{12}$
b)
$f(x)=\sqrt{3}$
$2\cdot \sqrt{3} \cdot sin(2x+\frac{\pi}{6})=\sqrt{3}$
$sin(2x+\frac{\pi}{6})=\frac{1}{2}$
$2x+\frac{\pi}{6}=sin^{-1}(\frac{1}{2})$
$2x+\frac{\pi}{6}=\frac{\pi}{6}+k\cdot 2\pi \quad \vee \quad 2x+\frac{\pi}{6}=\frac{5\pi}{6}+k\cdot 2\pi $
$x=k\pi \quad \vee \quad x=\frac{\pi}{3}+k\pi$
Den første løsningen er ikke i funksjonens definisjonområde og forkastes derfor. Den andre løsningen er gyldig for k=1:
$x=\frac{\pi}{3}$
c)
Funksjonen g er gitt ved:
$g(x)=3sin(2x)+\sqrt{3} cos(2x),\quad D_g=\langle0,2\pi\rangle$
Vi skal løse likningen $g(x)=\sqrt{3}$
Vi kan omforme likningen til en sinusfunksjon. Generelt har vi sammenhengen:
$a\,sin(kx)+ b\,cos(kx)=A\,sin(kx+\phi)$
hvor
$A=\sqrt{a^2+b^2}$
og
$tan\, \phi = \frac{b}{a}$
For g(x) har vi:
$A=\sqrt{3^2+\sqrt{3}^2}=\sqrt{12}=2\sqrt{3}$
$tan\,\phi=\frac{\sqrt{3}}{3}\quad \Rightarrow \quad \phi=\frac{\pi}{6}$
Da er $g(x)=2\cdot \sqrt{3} \cdot sin(2x+\frac{\pi}{6})=f(x)$
For likningen $g(x)=\sqrt{3}$, kan vi bruke løsningen fra oppgave b) i definisjonsområdet $D_g=\langle0,2\pi\rangle$
$x=k\pi \quad \vee \quad x=\frac{\pi}{3}+k\pi$
Den første løsningen er gyldig for k= 1, og den andre løsningen er gyldig for k=0 og k=1. Vi har:
$x=\frac{\pi}{3} \quad \vee \quad x=\pi \quad \vee \quad x=\frac{4\pi}{3}$
Oppgave 5
a)
$\vec{AB}=[2,3,0]$
$\vec{AC}=[1,4,1]$
$\vec{BA}=[-2,-3,0]$
$\vec{BC}=[-1,1,1]$
$\vec{CB}=[1,-1,-1]$
$\vec{CA}=[-1,-4,-1]$
$\vec{AB}\cdot \vec{AC}=2+12+1=15 \quad \Rightarrow \quad \angle A < 90^o$
$\vec{BA}\cdot \vec{BC}=2-3+0=-1 \quad \Rightarrow \quad \angle B > 90^o$
$\vec{CA}\cdot \vec{CB}=-1+4+1=4 \quad \Rightarrow \quad \angle C < 90^o$
Vinkel B er større enn 90 grader, fordi skalarproduktet til vinkelbeina er negativt (indikerer at cosinus til vinkelen er negativ, og vinkelen derfor er større enn 90 grader).
b)
Arealet av trekanten er halvparten av arealet utspent av to av sidene (to av vektorene).
$\vec{BA}\times\vec{BC} = \left| \begin{array}{ccc}i & j & k \\-2 & -3 & 0 \\-1 & 1 & 1 \end{array} \right | = [-3+0,0-(-2), -2-3] = [-3,2,-5]$
$A_{ABC}= \frac{1}{2} |[-3,2,-5]| = \frac{1}{2}\sqrt{(-3)^2+2^2+(-5)^2}=\frac{1}{2}\sqrt{9+4+25}=\frac{1}{2}\sqrt{38}$
c)
$\vec{DE}=[-1,-4,-1]$
Vi har en normalvektor til planet som trekant ABC ligger på, fra oppgave b): $ [-3,2,-5] $
Sjekker om normalvektoren til planet og linja står vinkelrett på hverandre, ved å sjekke om skalarproduktet blir 0:
$[-1,-4,-1]\cdot [-3,2,-5]=3-8+5=0$
Normalvektoren til planet og linja står vinkelrett på hverandre, som vil si at planet og linja er parallelle. Grenen vil aldri treffe bordplata.
Oppgave 6
Programmet summerer arealet av små rektangler med bredde dx og lengde f(x), pluss små rektangler med bredde dx og lengde g(x). Dette gjør programmet fra x = 0 til x = 2, med intervaller på 0.0001. Alle arealene summeres. Dette er det samme som summen av integralene til begge funksjonene fra x=0 til x=2.
$\int_0^2 f(x) dx = \int_0^2 x^3 dx = [\frac{1}{4}x^4]_0^2=(\frac{1}{4}\cdot 2^4)-(\frac{1}{4}\cdot 0^4)=\frac{1}{4}\cdot 16-0=4$
$\int_0^2 g(x) dx = \int_0^2 -2x^2 dx = [-\frac{2}{3}x^3]_0^2=(-\frac{2}{3}\cdot 2^3)-(-\frac{2}{3}\cdot 0^3)=-\frac{2}{3}\cdot 8-0=-\frac{16}{3}$
Summerer arealene:
$4+(-\frac{16}{3})=\frac{12}{3}-\frac{16}{3}=-\frac{4}{3}$
Programmet skriver ut $-\frac{4}{3}$, eller $-1,33333...$
Oppgave 7
a)
Buelengden L til en sirkelsektor er gitt ved: $L=2\pi r \cdot \frac{v}{360^o}$, hvor r er radiusen og v er vinkelen av sektoren.
Vi har:
$4=2\pi \cdot 3 \cdot \frac{v}{360^o}$
$v = \frac{4\cdot 360^o}{6\pi}$
$v = \frac{240^o}{\pi}$
Hvis vi runder av pi til ca. 3, vet vi at vinkelen er mindre enn 80 grader.
For radianer har vi at $L=r\cdot v$
Vi har:
$4=3\cdot v$
$v=\frac{4}{3}\approx 1,333...$
b)
$tan\,u=2$
$\frac{sin\,u}{cos\,u}=2$
$sin\,u=2cos\,u$
Setter inn verdien for sin u i enhetsformelen:
$sin^2 u + cos^2 u = 1$
$(2 cos\,u)^2 + cos^2 u=1$
$5 cos^2 u = 1$
$cos\,u = \pm\sqrt{\frac{1}{5}}=\pm\frac{\sqrt{5}}{5}$
$sin\, u = 2 cos\,u = \pm \frac{2\sqrt{5}}{5}$
Siden $u\in\langle0,\frac{\pi}{2}\rangle$, har vi $sin\,u=\frac{2\sqrt{5}}{5}$ og $cos\,u=\frac{\sqrt{5}}{5}$
DEL 2
Oppgave 1
a)
Bruker CAS i Geogebra.
Bilen er ca. 6,67 meter over bakkenivå etter 5 sekunder.
b)
Fartsvektoren er definert på linje 3.
Farten til bilen etter 10 sekunder er ca. 2,5 meter per sekund.
c)
Generelt er sinusfunksjoner gitt ved:
$f(x)=Asin(kx+\phi)+d$
For $\vec{r}(t)$ er $k=\frac{\pi}{5}$
Periode: $p=\frac{2\pi}{k}=\frac{2\pi}{\frac{\pi}{5}}=10$
En periode er på 10 sekunder. Finner høyden etter 10 sekunder, minus høyden ved start.
Høyden mellom etasjene kan være ca. 3,33 meter.
Oppgave 2
a)
Summen av sparingen er en geometrisk rekke hvor ledd nr. n er gitt ved $a_n=a_1\cdot k^n$
Summen av de n første leddene i denne geometriske rekka er gitt ved:
$S_n=a_1\cdot k\cdot\frac{k^n-1}{k-1}$
Her skal summen bli 3 750 000 kr, og k = 1,025.
Her er to forskjellige måter å beregne $a_1$ i CAS:
Nora må sette inn ca. 83 333 kr i banken hvert år for å nå målet.
b)
Bruker at summen av nåverdiene til terminbeløpet, skal bli lik lånebeløpet:
Nora har regnet med at den årlige rentesatsen på lånet er 3,5 %.
Oppgave 3
a)
Bruker CAS i Geogebra.
Det tar 0,97 sekunder før akselerasjonen til haren er null. Det forteller at haren har nådd toppfarten sin etter 0,97 sekunder (toppunkt på grafen til v).
b)
Haren løper 103,4 meter i løpet av de første 7 sekundene.
c)
Definerer funksjonen for gjennomsnittsfarten i linje 4. Finner ut hvor mange sekunder det tar for haren å løpe 200 meter i linje 5. Finner gjennomsnittsfarten etter 14,954 sekunder (200 meter) i linje 5.
Gjennomsnittsfarten til haren er 13,37 meter per sekund de første 200 meterne.
Oppgave 4
For en uendelig geometrisk rekke gitt ved $1+x+x^2+x^3+...$
har vi at
$\int 1\,dx + \int x\,dx + \int x^2\,dx + \int x^3\,dx + ... = \int \frac{1}{1-x} dx, \quad x\in \langle -1,1 \rangle$
Integrerer hvert ledd og får:
$x+\frac{1}{2}x^2+\frac{1}{3}x^3+\frac{1}{4}x^4+...=-ln|x-1|$
Jeg har brukt CAS til å integrere $\frac{1}{1-x}$, og ignorerer integrasjonskonstanten, slik det står i oppgaven at vi kan gjøre.
Vi har rekken
$\frac{1}{2^1}+\frac{1}{2}\cdot\frac{1}{2^2}+\frac{1}{3}\cdot\frac{1}{2^3}+\frac{1}{4}\cdot\frac{1}{2^4}+...$
som er den samme rekken som over, hvor $x=\frac{1}{2}$
Summen av denne rekken er altså
$-ln|\frac{1}{2}-1|=-ln(\frac{1}{2})=-(ln\,1-ln\,2)=0+ln\,2=ln\,2$