Koordinatsystem: Forskjell mellom sideversjoner
Ingen redigeringsforklaring |
Ingen redigeringsforklaring |
||
| Linje 1: | Linje 1: | ||
== Koordinatsystem == | |||
<div style="background:#f8f9fa; padding:20px; border-radius:8px; border:1px solid #dcdcdc;"> | |||
Et koordinatsystem består av to tallinjer som står vinkelrett på hverandre. Vi kaller disse tallinjene for '''akser'''. Punktet der aksene krysser hverandre kalles '''origo'''. Begge aksene har verdien null i origo. | |||
<br><br> | |||
Den vannrette aksen kalles '''x-aksen''' eller '''førsteaksen'''. | |||
Den loddrette aksen kalles '''y-aksen''' eller '''andreaksen'''. | |||
<br><br> | |||
Et punkt kan bestemmes med to tall (et tallpar) som vi kaller '''koordinater'''. Tallpar skrives på formen <math>(x, y)</math>. | |||
<br><br> | |||
Origo har koordinatene <math>(0,0)</math>. Man oppgir alltid x-verdien først. | |||
<br><br> | |||
Punktet <math>(1,3)</math> har verdiene <math>x = 1</math> og <math>y = 3</math>. | |||
</div> | |||
<br> | |||
=== Illustrasjon === | |||
[[Fil:Figen.png|center|500px|Et koordinatsystem med inntegnede punkter]] | |||
<br> | |||
<div style="background:#eef4ff; padding:20px; border-radius:8px; border-left:6px solid #2a6ebb;"> | |||
=== Eksempler på punkter === | |||
Her er eksempler på noen punkter: | |||
* <math>A(1,2)</math> | |||
* <math>B(4,0)</math> | |||
* <math>C(-1,-2)</math> | |||
* <math>D(-2,0)</math> | |||
</div> | |||
<br> | |||
På denne måten kan alle «steder» (punkter) i et plan representeres med en x-koordinat og en y-koordinat. | |||
<br><br> | |||
Alle [[kart]] er laget på denne måten. | |||
X-aksen er da øst–vest-retning og Y-aksen er nord–sør-retningen. | |||
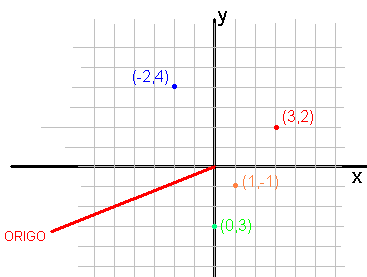
Et koordinatsystem i planet består av to akser (koordinatakser), x- aksen og Y- aksen. X-aksen er horisontal (vannrett) og y-aksen er vertikal (loddrett). Punktet der aksene krysser kalles for origo. Koordinatsystemet gir oss muligheten til å presentere punkter i planet i form av to tallverdier (x,y). Origo har koordinatene (0,0) Figur 1 nedenfor viser et koordinatsystem i planet. Et koordinatsystem i rommet utvides med en Z akse. Et punkt representeres med koordinatene (x,y,z), som vist i figur 2. | Et koordinatsystem i planet består av to akser (koordinatakser), x- aksen og Y- aksen. X-aksen er horisontal (vannrett) og y-aksen er vertikal (loddrett). Punktet der aksene krysser kalles for origo. Koordinatsystemet gir oss muligheten til å presentere punkter i planet i form av to tallverdier (x,y). Origo har koordinatene (0,0) Figur 1 nedenfor viser et koordinatsystem i planet. Et koordinatsystem i rommet utvides med en Z akse. Et punkt representeres med koordinatene (x,y,z), som vist i figur 2. | ||
Siste sideversjon per 16. feb. 2026 kl. 05:36
Koordinatsystem
Et koordinatsystem består av to tallinjer som står vinkelrett på hverandre. Vi kaller disse tallinjene for akser. Punktet der aksene krysser hverandre kalles origo. Begge aksene har verdien null i origo.
Den vannrette aksen kalles x-aksen eller førsteaksen. Den loddrette aksen kalles y-aksen eller andreaksen.
Et punkt kan bestemmes med to tall (et tallpar) som vi kaller koordinater. Tallpar skrives på formen <math>(x, y)</math>.
Origo har koordinatene <math>(0,0)</math>. Man oppgir alltid x-verdien først.
Punktet <math>(1,3)</math> har verdiene <math>x = 1</math> og <math>y = 3</math>.
Illustrasjon

Eksempler på punkter
Her er eksempler på noen punkter:
- <math>A(1,2)</math>
- <math>B(4,0)</math>
- <math>C(-1,-2)</math>
- <math>D(-2,0)</math>
På denne måten kan alle «steder» (punkter) i et plan representeres med en x-koordinat og en y-koordinat.
Alle kart er laget på denne måten. X-aksen er da øst–vest-retning og Y-aksen er nord–sør-retningen.
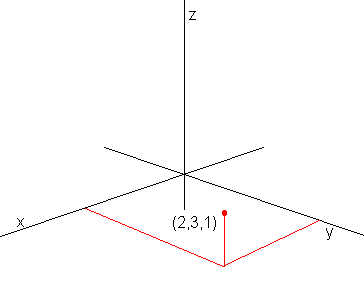
Et koordinatsystem i planet består av to akser (koordinatakser), x- aksen og Y- aksen. X-aksen er horisontal (vannrett) og y-aksen er vertikal (loddrett). Punktet der aksene krysser kalles for origo. Koordinatsystemet gir oss muligheten til å presentere punkter i planet i form av to tallverdier (x,y). Origo har koordinatene (0,0) Figur 1 nedenfor viser et koordinatsystem i planet. Et koordinatsystem i rommet utvides med en Z akse. Et punkt representeres med koordinatene (x,y,z), som vist i figur 2.
Figur 1: Koordinatsystem i planet (2D).
Figur 2: Koordinatsystem i rommet (3D).