Løsning del 2 10kl Vår 25: Forskjell mellom sideversjoner
| Linje 10: | Linje 10: | ||
====Oppgave 1==== | ====Oppgave 1==== | ||
| Linje 24: | Linje 24: | ||
=====c)===== | =====c)===== | ||
[[File:310525-04.png|500px]] | |||
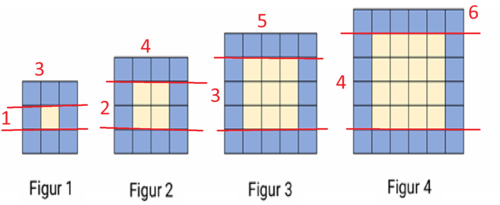
Blå ramme med kvadrater: Topp og bunn har to små kvadrater mer enn figur nummer altså n+2. Siden det er to (topp og bunn) får vi | |||
\[2(n+2) = 2n+4\] | |||
I tillegg har vi høyre og venstre side. Når vi fjerne det lille topp og bunn kvadratet får vi at antall småkvadrater er det samme som figurtallet på hver side, altså | |||
\[2n\] | |||
tilsammen, der n er figurtallet. | |||
Formel for små blå kvadrater blir da | |||
\[f(n) = 2n+4+2n = 4n+4\] | |||
====Oppgave 2==== | ====Oppgave 2==== | ||
Sideversjonen fra 1. jun. 2025 kl. 02:20
Oppgaven som pdf del 1 og del 2 samlet
Diskusjon av oppgaven på Matteprat
Løsningsforslag del 1 og del 2 laget av Fahan Omar
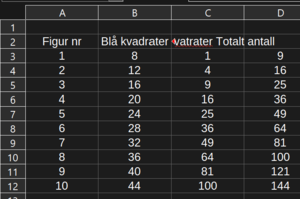
Oppgave 1
a)
For å finne figur nr. 5 må vi se litt på hvordan figurene endrer seg når vi går opp en størrelse. Figuren er et kvadrat som består av mindre kvadrater. Vi ser at sidekantene i det store kvadratet alltid består av to mer enn plassnummer. Figur nr. 3 er $5 \cdot 5$ og figur 4 består av $6 \cdot 6 =36$ små kvadrater. Figur nr. 5 vil da se slik ut:
b)
c)
Blå ramme med kvadrater: Topp og bunn har to små kvadrater mer enn figur nummer altså n+2. Siden det er to (topp og bunn) får vi
\[2(n+2) = 2n+4\]
I tillegg har vi høyre og venstre side. Når vi fjerne det lille topp og bunn kvadratet får vi at antall småkvadrater er det samme som figurtallet på hver side, altså \[2n\] tilsammen, der n er figurtallet.
Formel for små blå kvadrater blir da \[f(n) = 2n+4+2n = 4n+4\]