Løsning del 2 10kl Vår 25

Oppgaven som pdf del 1 og del 2 samlet

Sensorveiledning

Diskusjon av oppgaven på Matteprat

Løsningsforslag del 1 og del 2 laget av Fahan Omar

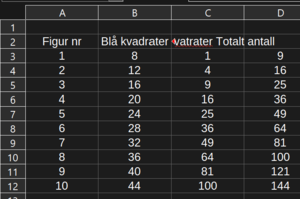
Oppgave 1

a)

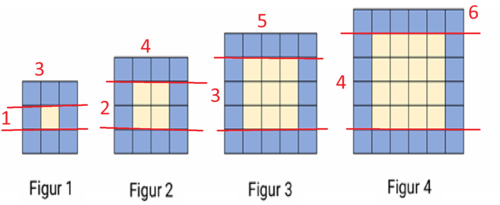
For å finne figur nr. 5 må vi se litt på hvordan figurene endrer seg når vi går opp en størrelse. Figuren er et kvadrat som består av mindre kvadrater. Vi ser at sidekantene i det store kvadratet alltid består av to mer enn plassnummer. Figur nr. 3 er $5 \cdot 5$ og figur 4 består av $6 \cdot 6 =36$ små kvadrater. Figur nr. 5 vil da se slik ut:

b)

c)

Blå ramme med kvadrater: Topp og bunn har to små kvadrater mer enn figur nummer altså n+2. Siden det er to (topp og bunn) får vi

\[2(n+2) = 2n+4\]

I tillegg har vi høyre og venstre side. Når vi fjerne det lille topp og bunn kvadratet får vi at antall småkvadrater er det samme som figurtallet på hver side, altså \[2n\] tilsammen, der n er figurtallet.

Formel for små blå kvadrater blir da \[f(n) = 2n+4+2n = 4n+4\]

Figur fire: \[f(4)= 4 \cdot 4 +4 = 20\]

Det er 20 blå kvadrater i figur 4. Vi ser at geometri og algebra stemmer.

Oppgave 2

Et par sokker koster 80 kroner.

Tilbud 1

6 par for 299kr. Det blir $\frac {299kr}{6par} \approx 50 kr/par$

Tilbud 2

25% rabatt. Det blir $80kr/par \cdot 0,75 = 60kr/par$

Tilbud 3

3 par til prisen for 2 par. Betaler 160kr for tre par, altså ca 53 kr per par.

Tilbud 4

50% på par nr. 3. Det betyr at man betaler 200kr for tre par, altså ca. 67 kr per par.

Dersom man kun tenker pris per par er tilbud nr. 1 best. Trenger man 6 par? Dersom nei er tilbud 3 ok.

Oppgave 3

a)

Eksponentiell vekst er vekst der størrelsen øker med en fast prosent hver tidsperiode.

\[f(x) = 20000 \cdot 1,04^x \]

• 20000 er startverdien
• 1,04 er vekstfaktoren når noe øker med 4%
• x er tidsperioden, i dette tilfelle år.

b)

Bruker Geogebra og finner at han har 36018,87 kr etter 15 år.

Oppgave 4

a)

Det er tre oddetall på en terning (1,3,5), og det er tre partall (2,4,6). Siden antall gunstige for begge er 3, av 6, altså 50% sjanse for det ene eller det andre, er dette rettferdig.

b)

To like:

g = gul

r = rosa

\[P(to_ like) = P(g) \cdot P(g) + P(r) \cdot P(r) = \frac 12 \cdot \frac 13 + \frac 12 \cdot \frac 13 = \frac 13\]

To ulike:

\[P(to_ ulike) = P(g) \cdot P(r) + P(r) \cdot P(g) = \frac 12 \cdot \frac 23 + \frac 12 \cdot \frac 23 = \frac 23\]

Oppgave 8

a, b og c)

Påstand 1

7 + 5 = 12

1 + 3 = 4

n er et tilfeldig heltall og m er et annet tilfeldig heltall. Da vil 2n og 2m være partall. (2n-1) og (2m-1) vil alltid være oddetall.

sum: (2n-1)+ (2m -1) = 2n + 2m - 2 = 2(n + m + 1)

Summen er alltid et partall og derved delelig på to.

Påstanden stemmer, alltid.

Påstand 2

3 + 4 = 7

11 + 12 = 23

Summen av to påfølgende heltall vil alltid være summen av et partall og et oddetall:

2n + 2n-1 = 4n-1

4n er et partall, (4n-1) er derfor et oddetall, alltid.

Påstanden er feil.

Påstand 3

3 + 4 + 5 = 12

4 + 5 + 6 = 15

Summen av tre påfølgende heltall vil være summen av (partall + oddetall + partall) eller (oddetall + partall + oddetall).

Dersom summen er to oddetall og ett partall:

(2n-1) + 2n + (2n + 1) = 6n = 2(3n), dvs. alltid partall

Dersom summen er to partall og ett oddetall:

2n + (2n + 1) + (2n + 2) = 6n +3 = 3(2n+1), som alltid er et oddetall.

Påstanden er riktig dersom man starter med et partall og feil dersom man starter med et oddetall.