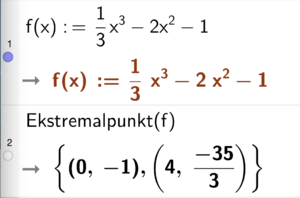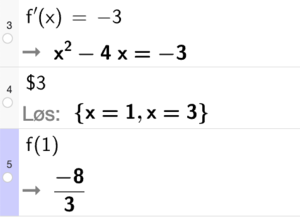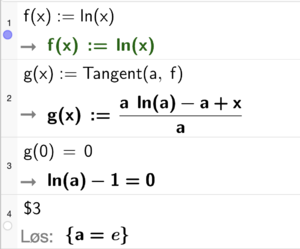R1 2025 Vår LØSNING

Oppgaven som pdf

Diskusjon av oppgaven på Matteprat

Del 1

Oppgave 1

Vi skal derivere funksjonen:

$$f(x)=e^{-2x}+\frac{1}{5}{x}^5-2\pi$$

Deriver ledd for ledd:

• $e^{-2x}\to -2e^{-2x}$
• $\frac{1}{5}{x}^5\to x^4$
• $-2\pi \to 0$, siden $\pi$ er konstant.

Svar: $$\underset{―}{\underset{―}{f^{\prime }(x)=-2e^{-2x}+x^4}}$$

Oppgave 2

Funksjonen er gitt som:

$$g(x)=\frac{1}{2}{e}^x(2x-1{)}^2$$

a) Nullpunkter

Vi setter $g(x)=0$:

$$\frac{1}{2}{e}^x(2x-1{)}^2=0$$

Siden $e^x\ne 0$, må:

$$(2x-1{)}^2=0\Rightarrow x=\frac{1}{2}$$

Nullpunkt: $\underset{―}{\underset{―}{x=\frac{1}{2}}}$

b) Derivere $g(x)$

Løsningsskisse (produktregel):

La:

• $u(x)=\frac{1}{2}{e}^x$

• $v(x)=(2x-1{)}^2$

Da:

$$g^{\prime }(x)=u^{\prime }(x)v(x)+u(x)v^{\prime }(x)$$ $$=\frac{1}{2}{e}^x(2x-1{)}^2+\frac{1}{2}{e}^x\cdot 2(2x-1)\cdot 2$$

$$=\frac{1}{2}{e}^x((2x-1{)}^2+4(2x-1))$$

Utvid og faktoriser uttrykket:

$$(2x-1{)}^2+4(2x-1)=(2x-1)(2x-1+4)=(2x-1)(2x+3)$$

Bekreftet: $$g^{\prime }(x)=\frac{1}{2}{e}^x(2x-1)(2x+3)$$

c) Topp- og bunnpunkter

Finn stasjonære punkter ved å løse $g^{\prime }(x)=0$:

$$\frac{1}{2}{e}^x(2x-1)(2x+3)=0$$

Løsning: $x=\frac{1}{2}$ og $x=-\frac{3}{2}$

Finn $g(x)$-verdiene:

• $g\left(\frac{1}{2}\right)=\frac{1}{2}{e}^{1/2}\cdot 0=0$

• $g(-\frac{3}{2})=\frac{1}{2}{e}^{-3/2}\cdot (-4{)}^2=\frac{1}{2}{e}^{-3/2}\cdot 16=8e^{-3/2}$

Svar:

• Bunnpunkt: $\underset{―}{\underset{―}{(\frac{1}{2},0)}}$

• Toppunkt: $\underset{―}{\underset{―}{(-\frac{3}{2},8e^{-3/2})}}$

Oppgave 3

a)

$$3^{3x+2}-5=76$$ $$3^{3x+2}=81=3^4$$ $$3x+2=4$$ $$\underset{―}{\underset{―}{x=\frac{2}{3}}}$$

b)

$$3\lg x+2\lg x^2+\lg \left(\frac{1}{x^9}\right)=2$$

Bruk logaritmeregler:

- $\lg x^2=2\lg x$

- $\lg \left(\frac{1}{x^9}\right)=\lg (1)-\lg (x^9)=-9\lg x$

Da får vi:

$$3\lg x+4\lg x-9\lg x=2$$ $$-2\lg x=2$$ $$\lg x=-1$$ $$x={10}^{-1}=\underset{―}{\underset{―}{0,1=\frac{1}{10}}}$$

Oppgave 4

a)

Direkte innsetting gir:

$$\frac{3(9-3)}{0}=\frac{18}{0}$$

Ikke av typen $\frac{0}{0}$ – som betyr at grenseverdien kan gå mot $+\mathrm{\infty }$, $-\mathrm{\infty }$ eller være udefinert.

Når $x\to 3^{-}$:

• Telleren nærmer seg $18$ og nevneren er negativ og nærmer seg $0$

• $\Rightarrow$ Brøken går mot $-\mathrm{\infty }$

Når $x\to 3^{+}$:

• Telleren nærmer seg $18$ og nevneren er positiv og nærmer seg $0$

• $\Rightarrow$ Brøken går mot $+\mathrm{\infty }$

Grenseverdien eksistere ikke.

b)

$$\underset{x\to 4}{lim}\frac{\sqrt{x}-2}{x-4}$$

Bruk konjugatsetning med $x-4$: $$\underset{x\to 4}{lim}\frac{\sqrt{x}-2}{(\sqrt{x}-2)(\sqrt{x}+2)}$$ $$\underset{x\to 4}{lim}=\frac{1}{\sqrt{x}+2}$$ $$=\frac{1}{\sqrt{4}+2}=\underset{―}{\underset{―}{\frac{1}{4}}}$$

Oppgave 5

Funksjon gitt som:

$$f(x)=\{\begin{array}{ll}{x}^2+2,& x<0\\ 2e^x,& x\ge 0\end{array}$$

a) Kontinuitet

Sjekk om grenser fra venstre og høyre i $x=0$ gir samme verdi:

• Venstre: $\underset{x\to 0^{-}}{lim}f(x)=0^2+2=2$
• Høyre: $\underset{x\to 0^{+}}{lim}f(x)=2e^0=2$

Funksjonen er kontinuerlig i $x=0$.

b) Deriverbarhet

Venstrederivert:

$$\underset{x\to 0^{-}}{lim}{f}^{\prime }(x)=\underset{x\to 0^{-}}{lim}2x=0$$

Høyrederivert:

$$\underset{x\to 0^{+}}{lim}{f}^{\prime }(x)=\underset{x\to 0^{+}}{lim}2e^x=2·e^0=2$$

Ulike verdier Ikke deriverbar i $x=0$

Oppgave 6

a) Avstand mellom Nils og Ahmad

$$\overrightarrow{NA}=[1-(-1),1-2]=[2,-1]$$ $$|\overrightarrow{NA}|=\sqrt{2^2+(-1{)}^2}$$ $$\underset{―}{\underset{―}{|\overrightarrow{NA}|=\sqrt{5}}}$$

b) Punktet $(-1,a)$ ligger på linjen fra Jelena som er parallell med $\overrightarrow{NA}$

La $P=(-1,a)$

• $\overrightarrow{NA}=(2,-1)$
• $\overrightarrow{JP}=(-1,a)$

Siden $\overrightarrow{JP}\parallel \overrightarrow{NA}$ kan vi skrive $t·\overrightarrow{NA}=\overrightarrow{JP}$

$$t[2,1]=[-1,a]$$ $$2t=-1\vee -t=a$$ $$t=-\frac{1}{2}\Rightarrow \underset{―}{\underset{―}{a=\frac{1}{2}}}$$

c) Finn punkt $M$

Finn punkt $M$ slik at:

• $|JM|=\sqrt{10}$
• $\mathrm{\angle }MAJ={90}^{\circ }$

Siden $\mathrm{\angle }MAJ={90}^{\circ }$ er $\overrightarrow{AM}\cdot \overrightarrow{JA}=0$

La $M=(x,y)$.

Siden $\overrightarrow{JM}=[x,y]$ og $|\overrightarrow{JM}|=\sqrt{10}\Rightarrow x^2+y^2=10$

• $\overrightarrow{AM}=(x-1,y-1)$
• $\overrightarrow{JA}=(1,1)$

$$\overrightarrow{AM}\cdot \overrightarrow{JA}=x-1+y-1=0$$ $$x+y=2\Rightarrow y=2-x$$

Sett $y=2-x$ inn $x^2+y^2=10$:

$$x^2+(2-x{)}^2=10\Rightarrow x^2+4-4x+x^2=10\Rightarrow 2x^2-4x-6=0$$

Løs:

$$\begin{gathered} x=3\Rightarrow y=-1 \\ x=-1\Rightarrow y=3 \end{gathered}$$

Svar: Mulige punkter: $M=(-1,3)$ og $M=(3,-1)$

Del 2

Oppgave 1

a) Hvor lang tid vil det ta før halvparten av husstandene har batteriet?

Vi skal finne $t$ slik at $S(t)=1250000$, altså halvparten av maksverdien $2500000$.

• Linje 1: Funksjonen $S$ defineres som:

$$S(t):=\frac{2500000}{1+2500\cdot e^{-0.08t}}$$

• Linje 2: Likningen $S(t)=1250000$ løses, og vi får:

$$t\approx 97.8$$

Dette betyr at det vil ta omtrent 97,8 uker før halvparten av husstandene har batteriet.

Alternativ fremgangsmåte:

• Alternativt bekreftes dette ved å bruke `Vendepunkt(S)`, som gir punktet $(97.8,1250000)$ – altså vendepunktet for den logistiske modellen.

b) Bestem $S^{\prime }(52)$ og gi en praktisk tolkning

• Bildet viser at den deriverte ved $t=52$ er:

$$S^{\prime }(52)\approx 4872.76$$

Tolkning: Ved uke 52 øker antallet husstander med batteriet med omtrent 4873 husstander per uke.

c) Finn en justert logistisk modell

Vi skal finne en ny modell på formen:

$$F(t)=\frac{N}{1+a\cdot e^{-kt}}$$

Gitt:

• $N=1500000$, siden $F(t)\to 1500000$ etter lang tid
• $F(0)=500$
• Vendepunkt ved $t=60$, altså $F(60)=750000$

Trinn 1: Bestem $a$

• Opprinnelig definisjon av $F(t)$ på linje 5
• På linje 6 settes $F(0)=500$:

$$\frac{1500000}{a+1}=500\Rightarrow a=2999$$

Trinn 2: Bestem $k$

• I bildet over var de tidligere linje 6 og 7 slettet, og funksjonen på linje 5 blitt oppdatert med verdien $a=2999$:

$$F(t)=\frac{1500000}{2999\cdot e^{-kt}+1}$$

• På linje 6, settes $F(60)=750000$ og løses:

$$\frac{1500000}{2999\cdot e^{-60k}+1}=750000\Rightarrow k=\frac{1}{60}\ln (2999)\approx 0.133$$

Alternativ metode

• I bildet over brukes vendepunktbetingelsen $F(60) = 0$foråløseut$k$.
• Også her får vi $k\approx 0.133$, som bekrefter riktig valg.

Endelig modell:

$$\underset{―}{\underset{―}{F(t)=\frac{1500000}{1+2999\cdot e^{-0.133t}}}}$$

Dette er den justerte logistiske modellen som tar høyde for BA3s konkurranse og gir korrekt vekstmønster med oppgitt startverdi og vendepunkt.

Oppgave 2

a) Bestem intervallet $I$, slik at $f$ har ein omvend funksjon

Vi ønsker at funksjonen $f(x)=\frac{1}{3}{x}^3-2x^2-1$ skal være én-til-én i et intervall som inneholder $x=2$. Dette oppnås hvis $f$ er strengt voksende eller strengt minkende i hele intervallet.

Dette kan vi bestemmer ved å finne ekstremalpunkter i CAS:

• Linje 1: Funksjonen $f$ er definert.
• Linje 2: Kommandoen Ekstremalpunkt(f) finner topp- og bunnpunkt:

$f$ har ekstremalpunkt i $x=0\text{ og }x=4$

Dermed er funksjonen strengt minkende på $[0,4]$, og dette er det største intervallet som inneholder $x=2$ og hvor $f$ er én-entydige.

Svar: $$\underset{―}{\underset{―}{I=[0,4]}}$$

b) Bestem stigningstallet til tangenten til grafen til $g$ i punktet $(-10,3)$

Punktet $(-10,3)$ ligger på grafen til $g$, altså $g(-10)=3\Rightarrow f(3)=-10$.

Vi finner $f^{\prime }(3)$ i CAS:

Stigningstallet til $g$ i dette punktet er den inverse av $f^{\prime }$ i punktet med samme $x$-verdi som $g$ sitt $y$-verdi:

$$g^{\prime }(-10)=\frac{1}{f^{\prime }(3)}=\frac{1}{-3}$$

Svar: Stigningstallet er $-\frac{1}{3}$

Alternativ metode: Finn tangenten til $f$ i $x=3$ (Tangent kommandoen) og bruk kommandoen Invers for å finne den inverse linjen.

c) Bestem koordinatene til tangeringspunktet, med samme stigning som i (b)

Vi ønsker et punkt på grafen til $g$ der tangenten har samme stigning som i (b), altså $g^{\prime }=-\frac{1}{3}$

Siden $g^{\prime }(x)=\frac{1}{f^{\prime }(g(x))}$, gjelder:

$$\frac{1}{f^{\prime }(x)}=-\frac{1}{3}\Rightarrow f^{\prime }(x)=-3$$

• Linje 3+4: Vi løser $f^{\prime }(x)=-3$ og finner:

$$x=1\text{og}x=3$$

Vi kjenner allerede punktet $(3,-10)$.

• Linje 5: Det andre punktet er:

$$x=1\Rightarrow f(1)=-\frac{8}{3}$$

Dermed er punktet på $f$: $$(1,-\frac{8}{3})$$

På grafen til $g$ blir dette punktet: $$(-\frac{8}{3},1)$$

Svar: $$\underset{―}{\underset{―}{(-\frac{8}{3},1)}}$$

Oppgave 3

Løsemåte i CAS:

Forklaring

Vi bruker navnene $p(x)$, $q(x)$ og $r(x)$ som egendefinerte betegnelser for de tre delene av funksjonen, for å gjøre beregningene tydeligere der

$$f(x)=\{\begin{array}{ll}p(x),& x\le -2\\ q(x),& -2<x<1\\ r(x),& x\ge 1\end{array}$$

$p(x)$ og $r(x)$ er gitt i oppgave, men siden $q$ er et ubestemt tredjegradspolynom kan vi bruke:

$$q(x)=a{x}^3+b{x}^2+cx+d$$

• Linje 1-3: Definere $p$, $q$ og $r$ i CAS

Vi ønsker å finne uttrykket for $q(x)$ slik at $f$ er kontinuerlig og deriverbar i hele $\mathbb{R}$. Siden alle $p$, $q$ og $r$ er polynomer, er det bare nødvendig å sjekke i delingspunktene til $f$:

For $x=-2$:

• Kontinuerlig dersom $\underset{x\to -2^{-}}{lim}f(x)=\underset{x\to -2^{+}}{lim}f(x)\Rightarrow p(-2)=q(-2)$
• Deriverbar dersom $\underset{x\to -2^{-}}{lim}{f}^{\prime }(x)=\underset{x\to -2^{+}}{lim}{f}^{\prime }(x)\Rightarrow p^{\prime }(-2)=q^{\prime }(-2)$

I CAS skrives det:

• Linje 4: $p(-2)=q(-2)$
  • Obs! Selv om $q(-2)$ ikke er definert som funksjonsverdi (siden $q$ bare gjelder for $-2<x<1$), kan vi likevel bruke uttrykket $q(-2)$ i CAS for å representere høyre grenseverdi.*

• Linje 5: $p^{\prime }(-2)=q^{\prime }(-2)$

For $x=1$:

• Kontinuerlig dersom $\underset{x\to 1^{-}}{lim}f(x)=\underset{x\to 1^{+}}{lim}f(x)\Rightarrow q(1)=r(1)$
• Deriverbar dersom: $\underset{x\to 1^{-}}{lim}{f}^{\prime }(x)=\underset{x\to 1^{+}}{lim}{f}^{\prime }(x)\Rightarrow q^{\prime }(1)=r^{\prime }(1)$

I CAS skrives det:

• Linje 6: $q(1)=r(1)$
• Linje 7: $q^{\prime }(1)=r^{\prime }(1)$

Linjer 4–7 utgjør et likningssystem.

• Linje 8: Løsning til likningssystemet:

$$\begin{array}{rl}a& =-\frac{13}{27}\\ b& =\frac{7}{9}\\ c& =-\frac{1}{9}\\ d& =-\frac{113}{27}\end{array}$$

Svar

Det manglende uttrykket i midten av $f(x)$ er:

$$q(x)=-\frac{13}{27}{x}^3+\frac{7}{9}{x}^2-\frac{1}{9}x-\frac{113}{27},\text{for }-2<x<1$$

Oppgave 4

a) Bestem farten til fiskebåten i knop

Vi har posisjonsvektoren:

$$\overrightarrow{r}(t)=[1+5t,4+8t]$$

• Linje 1: Posisjon uttrykkes som vektor
• Linje 2: Farten finnes som den deriverte:

$$\overrightarrow{v}(t)={\overrightarrow{r}}^{\prime }(t)=[5,8]$$

• Linje 3: Finne farten i km/h, ved å regne ut fartsvektorens lengde:

$$|\overrightarrow{v}|=\sqrt{5^2+8^2}=\sqrt{89}\approx 9.43$$

• Linje 4: Omregnet til knop ved å dele farten i km/h på $1.852$:

$$\frac{9.43}{1.852}\approx 5.09$$

Svar: Farten til fiskebåten er ca. $\underset{―}{\underset{―}{5,09\text{ knop}}}$

---

b) Bestem den minste avstanden mellom fiskebåten og fyret

Fyret står i punktet $(4,7)$.

• Linje 2: Punktet defineres i CAS som $T=(4,7)$
• Linje 3: Avstanden mellom båten og fyret uttrykkes som en funksjon $d(t)$:

$$d(t)=\sqrt{(5t+1-4{)}^2+(8t+4-7{)}^2}$$ CAS forenkler dette til: $$d(t)=\sqrt{89t^2-78t+18}$$

• Linje 4: Ekstremalpunkt for $d(t)$ viser at minste avstand oppstår når:

$$d_{\text{min}}\approx 0.954\text{ km}=954\text{ meter}$$

Svar: Minste avstand er $\underset{―}{\underset{―}{\text{954 meter}}}$

---

c) Vil fiskebåten treffe fiskestimen?

Fiskestimen er i punktet $(1,-3)$ ved tiden $t=0$ og svømmer med konstant hastighet $\overrightarrow{v}=[4,11]$. Vi bruker denne informasjonen for å definere en ny parametrisk funksjon $F$ som beskriver fiskestimens posisjon over tid:

$$F(t)=[1,-3]+t[4,11]=[1+4t,-3+11t]$$

Fremgangsmåte i CAS

• Linje 2: Definerer $F(t)$ som fiskestimens posisjon
• Linje 3: Forsøker å løse $F(t)=r(t)$ – altså om de befinner seg på samme sted samtidig
  • Resultat: $\{\}$ ⇒ ingen løsning*
• Linje 3+4: Løser $F(t)=r(s)$ for to ulike tidspunkter og får:

$$t=\frac{35}{23},s=\frac{28}{23}$$

Dette viser at de befinner seg i samme punkt, men på forskjellige tidspunkt.

Svar: Nei, fiskebåten treffer ikke fiskestimen – de er på samme sted til ulike tider.

---

d) Bestem farten fiskebåten må holde for å treffe fiskestimen

Fiskebåten starter i $(-2,0)$ og skal holde konstant fart i retning av vektoren $\overrightarrow{u}=(6,4)$.

Mens vi vet retning $\overrightarrow{u}$, vet vi ikke hvor stor farten er, så for å uttrykke hvor mye båten beveger seg per time må vi gange retning $\overrightarrow{u}$ med en ukjent skalar faktor $k>0$.

Tidsvariabelen $t$ representerer antall timer etter start, og multipliseres inn for å uttrykke hvor langt båten har beveget seg langs vektoren $\overrightarrow{u}$ etter $t$ timer.

Vi bruker dette for å lage en egendefinert funksjon $B$ som beskriver fiskebåtens posisjon:

$$B(t)=[-2,0]+k·t·[6,4]=[6·k·t-2,4·k·t]$$

CAS-løsning

• Linje 1–2: Definerer $F(t)$ og $B(t)$
• Linje 3–4: Løser $F(t)=B(t)$ for $t$ og $k$

Resultatet er: $$k=\frac{3}{2},t=\frac{3}{5}$$

Farten til fiskebåten (som lengden av fartsvektoren) er da $k\cdot |\overrightarrow{u}|$

Farten til fiskebåten blir:

$$k\cdot |\overrightarrow{u}|=3\sqrt{13}\approx 10.817$$

Svar: Fiskebåten må holde en fart på $\underset{―}{\underset{―}{10,82\text{ km/h}}}$

Oppgave 5

a) Bestem eksakte verdier for koordinatene til punktet B

Metode 1: Finn ved hjelp av gjennomsnittlig vekstfart

Dersom tangenten på B krysser gjennom A(0,0) skal gjennomsnittlig vekstfart i x-intervallet mellom 0 og B være lik momentanvekstfart i B:

• Linje 2: Løs for å finne $f$ da $\text{gvf}=\text{mvf}$

Metode 2: Finne tangent i et vilkårlig punkt $x=a$

Løs $g(0)=0$ slik at vi finner $a$ der $g$ har ingen konstantledd:

$$f(e)=1$$

Koordinatpunkt = $(e,1)$

b) Bestem det eksakte arealet av trekant ABC

Vi kjenner:

• $A=(0,0)$
• $B=(e,1)$
• Punkt $C$ ligger på linja $y=x$, og $\mathrm{\angle }ACB={90}^{\circ }$

Metode 1: Vektorer og skalarprodukt

La $C=(x,x)$. Altså et vilkårlig punkt på $y=x$

• Beregn $\overrightarrow{AC}$ og $\overrightarrow{BC}$
• Løs $\overrightarrow{AC}\cdot \overrightarrow{BC}=0$ for å sikre rett vinkel i $C$

• Linje 2-4: Definer punkt A og B og C
• Linje 5: Bruk Vektor(A,C) for å får vektoruttrykket for $\overrightarrow{AC}$
• Linje 6: Bruk Vektor(B,C) for å får vektoruttrykket for $\overrightarrow{BC}$
• Linje 7: Likningen til $\overrightarrow{AC}·\overrightarrow{BC}=0$
• Linje 8: Løs $\overrightarrow{AC}·\overrightarrow{BC}=0$ for å finne $x$ slik at $\overrightarrow{AC}$ og $\overrightarrow{BC}$ står vinkelrett

Vi får:

$$x=\frac{1}{2}(e+1)\Rightarrow C=(\frac{e+1}{2},\frac{e+1}{2})$$

• Linje 9: Vi definere et nytt punkt $C_1$ som har koordinatene funnet over
• Linje 10: Vi bestemme arealet til trekanten: $\text{Areal}=\frac{ABBC}{2}$

Svar: $$\underset{―}{\underset{―}{\text{Arealet til }\mathrm{△}ABC=\frac{1}{4}{e}^2-\frac{1}{4}}}$$

Eller:

Metode 2: Bruke NormalLinje-kommando

• Finn en linje gjennom $B$ som står normalt på $y=x$
• Finn skjæringspunktet $C$ mellom denne linja og $y=x$
• Bruk avstandsformler og determinanter til å finne areal

Gir samme punkt $C$ og areal:

$$\underset{―}{\underset{―}{\text{Arealet til }\mathrm{△}ABC=\frac{1}{4}{e}^2-\frac{1}{4}}}$$