Polynomdivisjon

Polynomdivisjon kan blant annet brukes til å faktorisere og forenkle et brøkuttrykk.

Nedenfor følger et eksempel på polynomdivisjon.

Eksempel 1

$(8 x^{4} + 10 x^{3} + 3 x^{2} + 2 x + 1) : (2 x + 1) =$
Tanken er som følger: Hva må 2x multipliseres med for at vi skal få 8x⁴? Svaret er 4x³som skrives på høyre side av likhetstegnet. 4x³ må også multipliseres med 1.
$(8 x^{4} + 10 x^{3} + 3 x^{2} + 2 x + 1) : (2 x + 1) = 4 x^{3} 8 x^{4} + 4 x^{3}$
Man trekker fra som ved vanlig divisjon og får:

<math>\qquad (8x^4+10x^3+3x^2+2x+1):(2x+1)= 4x^3 \ -(8x^4+4x^3) \ \qquad\qquad\qquad\qquad\qquad 6x^3+3x^2+2x+1 \ \qquad\qquad \qquad
</math>
Slik fortsetter man og får:

<math>\qquad (8x^4+10x^3+3x^2+2x+1):(2x+1)= 4x^3 +3x^2 + 1\ -(8x^4+4x^3) \ \qquad\qquad\qquad\qquad\qquad6x^3+3x^2+2x+1 \ \qquad\qquad\qquad\qquad-(6x^3+3x^2) \ \qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad 2x + 1 \ \qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad -(2x + 1) \ \qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad 0 \
</math>

I dette tilfellet ble resten null. De betyr at divisjonen gikk opp.

La oss se på et eksempel der divisjonen ikke går opp. Det betyr at man får en rest.

Eksempel 2

<math>\qquad(t^3 - 4t^2 - 8t + 13):(t-1)= t^2 -3t - 11 + \frac{2}{t-1} \ -(t^3-t^2) \ \qquad\qquad\qquad -3t^2 - 8t + 13 \ \qquad\qquad -(-3t^2 + 3t) \ \qquad\qquad \qquad\qquad\qquad\qquad\qquad-11t + 13 \ \qquad\qquad \qquad\qquad\qquad-(-11t + 11) \
\qquad\qquad \qquad\qquad\qquad\qquad\qquad \qquad \qquad \qquad\qquad2 \</math>

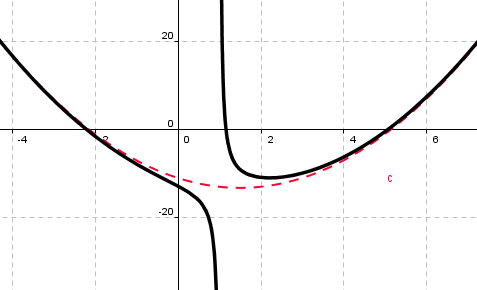
Resten i dette eksempelet blir 2. Nedenfor ser du funksjonen til $f (t) = \frac{t^{3} - 4 t^{2} - 8 t + 13}{t - 1}$ . Man observerer at
$g (t) = t^{2} - 3 t - 11$ er en asymptote til f(t). I tillegg er t = 1 en vertikal asymptote til f. Grafen til g er stiplet rød.

$\frac{P (x)}{Q (x)}$
Både P og Q er polynomer. Når man utfører divisjonen blir resten av lavere grad enn Q.

Når man dividerer polynomet P(x) med $(x - x_{0})$ blir resten $r = P (x_{0})$

P(x) er et polynom. Dersom P(x) har faktoren $(x - x_{0}) \Leftrightarrow P (x_{0}) = 0$

P(x) er et polynom. Dersom divisjonen $P (x) : (x - x_{0})$ går opp $\Leftrightarrow P (x_{0}) = 0$

Eksempel 3
Er (x+1) en faktor i polynomet $P (x) = 2 x^{3} - 2 x^{2} - 3 x + 1$ ?
Da må P(-1)= 0
Man får - 2 - 2 + 3 + 1 = 0
(x+1) er en faktor i P

Det betyr også at divisjonen P:(x+1) går opp.