R1 2011 høst LØSNING

DEL EN

a

1)
$$\begin{gathered} f(t)=0,02t^3+0,6t^2+4,1 \\ {f}^{\prime }(t)=0,06t^2+1,2t \end{gathered}$$

2)
$$\begin{gathered} g(x)=\sqrt{x^2-1} \\ {g}^{\prime }(x)=\frac{1}{2\sqrt{x^2-1}}\cdot 2x=\frac{x}{\sqrt{x^2-1}} \end{gathered}$$
3)
$$\begin{gathered} h(x)=x^2\cdot e^{2x} \\ {h}^{\prime }(x)=2x\cdot e^{2x}+x^2\cdot 2\cdot e^{2x}=2x{e}^{2x}(1+x) \end{gathered}$$

b

1)

$P(2)=2^3-4\cdot 2^2-4\cdot 2+16=8-16-8+16=0$

Siden P(2) = 0 er x=2 et nullpunkt.

2)

$$\begin{gathered} (x^3-4x^2-4x+16):(x-2)=x^2-2x-8 \\ -(x^3-2x^2) \\ -2X^2-4x \\ -(-2x^2+4x) \\ -8x+16 \\ -(-8x+16) \end{gathered}$$

$$\begin{gathered} x^2-2x-8=0 \\ x=\frac{2\pm \sqrt{4+32}}{2} \\ X=-2\vee x=4 \end{gathered}$$

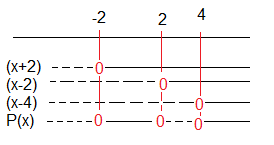
$x^3-4x^2-4x+16=(x-2)(x+2)(x-4)$

3)

$P(x)\le 0$

$x\in <\leftarrow ,-2]\cup [2,4]$

c

$$\begin{gathered} y=a-b^x \\ {b}^x=a-y \\ x=\frac{lg(a-y)}{lgb} \end{gathered}$$

y må være mindre enn a fordi man ikke kan ta logaritmen til et negativt tall.

d

1)

$$\begin{gathered} \overrightarrow{AB}=[3-1,4-0]=[2,4] \\ \overrightarrow{AC}=[2-1,t-0]=[1,t] \end{gathered}$$

2)

$$\begin{gathered} \overrightarrow{AB}\perp \overrightarrow{AC} \\ \overrightarrow{AB}\cdot \overrightarrow{AC}=0 \\ [2,4]\cdot [1,t]=0 \\ 2+4t=0 \\ t=-\frac{1}{2} \end{gathered}$$

3)

Dersom sirkelen ha AB som diameter er koordinatene til sentrum i sirkelen:

$$\begin{gathered} x=\frac{1+3}{2}=2 \\ y=\frac{0+4}{2}=2 \\ (2,2) \end{gathered}$$

Radius i sirkelen er en halv ganger lengden av AB vektor. $\frac{1}{2}|\overrightarrow{AB}|=\frac{\sqrt{20}}{2}$

e)

1)

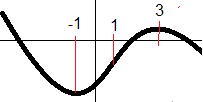
f minker i områdene minus uendelig til -1 og fra 3 til uendelig

f vokser fra -1 til 3.

2)

f har to ekstremalpunkt, et minimumspunkt for x = -1 og et maksimumspunkt for x = 3. Grafen har et vendepunkt for x=1. For verdier mindre enn 1 vender grafen sin hule side opp, og for verdier større enn 1 vender den sin hule side ned.

3)

f)

$$\begin{gathered} f(x)=x^2+1 \\ f´(x)=\underset{\mathrm{\Delta }x\to 0}{lim}\frac{f(x+\mathrm{\Delta }x)-f(x)}{\mathrm{\Delta }x} \\ =\underset{\mathrm{\Delta }x\to 0}{lim}\frac{((x+\mathrm{\Delta }x{)}^2+1)-(x^2+1)}{\mathrm{\Delta }x} \\ =\underset{\mathrm{\Delta }x\to 0}{lim}\frac{x^2+2x\mathrm{\Delta }x+(\mathrm{\Delta }x{)}^2+1-x^2-1}{\mathrm{\Delta }x} \\ =\underset{\mathrm{\Delta }x\to 0}{lim}\frac{\mathrm{\Delta }x(2x+\mathrm{\Delta }x)}{\mathrm{\Delta }x} \\ =\underset{\mathrm{\Delta }x\to 0}{lim}2x+\mathrm{\Delta }x=2x \end{gathered}$$

g)

1)

Vinkel ADB er en pereferivinkel og skjærer over samme bue som AOB. Vinkel ADB er defor ${30}^{\circ }$.

2)

Vinkel DBE er en pereferivinkel som spenner over samme bue som DOE. Vinkel DBE er derfor ${10}^{\circ }$ .

3)

Vinkelsummen i en trekant er 180 grader. I trekanten BCD er vinkel DBC 10 grader. Vinkel BDC er 180 - 30 = 150 grader. Vinkel ACB må da vare lik 20 grader.

DEL TO

a)

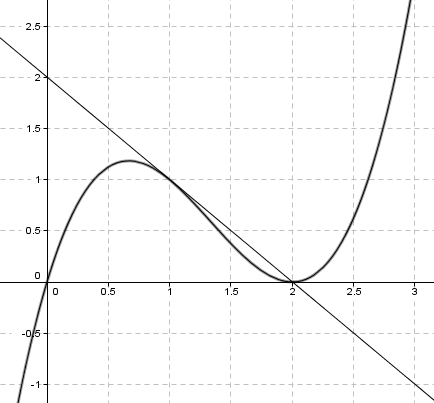
$$\begin{gathered} f(x)=x^3-4x^2+4xx\in <-1,3> \\ f(x)=0 \\ {x}^3-4x^2+4x=0 \\ x(x^2-4x+4)=0 \\ x=0\vee x^2-4x+4=0 \\ x=0\vee x=\frac{-(-4)\pm \sqrt{(-4{)}^2-4\cdot 1\cdot 4}}{2}=2 \end{gathered}$$

Summen under rottegnet i andregradsformelen er null. Det gir sammenfallende løsning for x = 2, hvilket betyr at grafen til f tangerer x-aksen i punktet (2,0)

b)

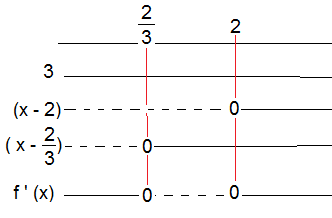
$$\begin{gathered} f^{\prime }(x)=3x^2-8x+4 \\ {f}^{\prime }(x)=0 \\ x=\frac{8\pm \sqrt{64-48}}{6} \\ x=\frac{8\pm 4}{6} \\ x=\frac{2}{3}\vee x=2 \\ {f}^{\prime }(x)=3(x-\frac{3}{2})(x-2) \end{gathered}$$

Grafen har et maksimumspunkt for $x=\frac{2}{3}$ og et minimumspunkt for x = 2.

Maksimumspunkt: $(\frac{2}{3},f(\frac{2}{3}))$ dvs $(\frac{2}{3},\frac{32}{27})$

Minimumspunkt: $(2,f(2))$ dvs. $(2,0)$

c)

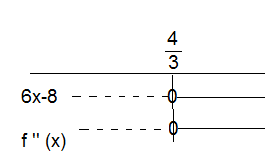
$$\begin{gathered} f^{″}(x)=6x-8 \\ {f}^{″}(x)=0 \\ 6x-8=0 \\ x=\frac{4}{3} \end{gathered}$$

Grafen til f vender sin hule side ned for x- verdier mindre enn $\frac{4}{3}$ og sin hule side opp for x- verdier støre enn $\frac{4}{3}$.

Vende punkt i $(\frac{4}{3},f(\frac{4}{3}))$ som er $(\frac{4}{3},\frac{16}{27})$.

d)

$$\begin{gathered} f(1)=1 \\ {f}^{\prime }(1)=-1 \\ y=ax+b \\ 1=-1+b \\ b=2 \\ y=-x+2 \end{gathered}$$

e)

f)

f(x) = -x+2

Med digitale hjelpemiddler ser man at denne likningen har løsning for x = 1 eller x = 2. f(2) = 0, dvs. Q har koordinatene (2,0)

a)

	Jenter	Gutter	Totalt
Bukse	60	80	140
Ikke Bukse	60	0	60
Total	120	80	200

$P(bukse)=\frac{140}{200}=0,70=70$ %

b)

$Pbukse|jente)=\frac{60}{120}=0,50=50$ %

$P(bukse|jente)\ne P(bukse)$. Det betyr at hendelsene er avhengige.

c)

Det står i oppgaven at man skal bruke Bayes formel, men når tallene er organisert i en krysstabell kan det være lettere å plukke sannsynligheten direkt fra tabellen. Vi skal finne sannsynligheten for jente gitt at personen går i bukser.

$P(jente|bukser)=\frac{60}{140}=0,429=42,9$ %

Dersom man bruker Bayes formel får man $P(jente|bukser)=\frac{P(jente)\cdot P(bukse|jente)}{P(bukser)}=\frac{0,6\cdot 0,5}{0,7}=0,429=42,9$%

a)

Faktorene som går opp i 28 er 1, 2, 4, 7 og 14. Summen er 1 + 2 + 4 + 7 + 14 = 28. Derfor er 28 det man kaller et perfekt tall.

b)

Faktorene som går opp i 284 er 1, 2, 4, 71 og 142. Summen av disse er 220. Man legger merke til at summen av faktorene i 220 er 284 og summen av faktorene i 284 er 220.