Løsning del 1 og del 2 utrinn Vår 16

Del 1 oppgave som pdf

Del 2 oppgave som pdf

Løsningsforslag fra MKH

Del 1

Oppgave 1

a

$856+173=1029$

b

$701-129=572$

c

$102\cdot 98=9996$

d

$624:3=208$

Oppgave 2

a

$4550$ mm = $455,0$ cm = $45,50$ dm = $4,550$ m

b

$0,8kg=8,0hg=800g$

Oppgave 3

$$\begin{gathered} (-3{)}^2=9 \\ \frac{20}{2+3}=4 \\ 2+2^2=6 \\ -2^2+6=-4+6=2 \end{gathered}$$

Det siste uttrykket har den laveste verdien.

Oppgave 4

a

$\frac{1}{6}+\frac{2}{6}=\frac{3}{6}=\frac{1}{2}$

b

$\frac{4}{5}-0,4=\frac{4}{5}-\frac{2}{5}=\frac{2}{5}$

Oppgave 5

Det tallet som har det høyeste sifferet på tidelsplassen er størst, altså 0,9.

Oppgave 6

$0,00000000000000000000000000000091kg=9,1\cdot {10}^{-31}kg$

Oppgave 7

f skjærer y-aksen i -1 og stiger med 1: f(x) = x - 1

g skjærer y-aksen i 2 og synker med en halv: $g(x)=-\frac{1}{2}x+2$

Oppgave 8

$3500kr\cdot 0,8=2800kr$

Alternativt: $3500kr-\frac{3500\cdot 20}{100}kr=2800kr$

Sykkelen koster 2800 kroner når rabatten er trukket fra.

Oppgave 9

Det er to gunstige av seks, altså $\frac{2}{6}$ som forkortes til $\frac{1}{3}$

Oppgave 10

6 + 4 = 10

5 + 5 = 10

4 + 6 = 10

3 av 36 utfall gir sum 10, altså $\frac{3}{36}=\frac{1}{12}$

Oppgave 11

a

$$\begin{gathered} 4x-3=x \\ 4x-x=3 \\ 3x=3 \\ x=1 \end{gathered}$$

b

$$\begin{gathered} \frac{x-1}{2}-x=3 \\ x-1-2x=6 \\ -x=7 \\ x=-7 \end{gathered}$$

Oppgave 12

a

-a + 2a + 3a = 4a

b

$\frac{1}{a-1}-\frac{1}{a+1}=\frac{(a+1)-(a-1)}{(a-1)(a+1)}=\frac{2}{a^2-1}$

Oppgave 13

$\frac{6}{0,2}$ er det samme som $\frac{60}{2}=30$.

Posen varer 30 dager, eller ca en måned.

Oppgave 14

Trekantene er formlike fordi vinklene i trekantene er parvis like store.

Oppgave 15

Toget bruker 6:34 etter midnatt. Før midnatt bruker toget 1:14. Den totale tiden blir da 7 h 48 min.

Oppgave 16

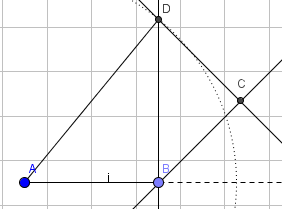
Avsetter AB lik 6 cm.

Konstruerer 90 grader i B

Avsetter 9,5 cm i passeren, setter spissen i A og finner punkt D.

Konstruerer 45 grader i B og D, i forhold til linjestykket BD, og finner C. Vinkel ABC er 135 grader, altså 90 + 45 og det er oppgitt at lengden av BC er lik lengden av CD, da må også vinkel BDC være 45 grader.

Oppgave 17

$$\begin{gathered} A=\frac{g\cdot h}{2} \\ 2A=g\cdot h \\ h=\frac{2A}{g} \end{gathered}$$

Oppgave 18

a

Pytagoras : BC = $\sqrt{{40}^2+{30}^2}=50$

BC er altså 50 meter.

b

Løpefart: $v_l=\frac{100m}{20s}=5m/s$

Svømmefart: $v_s=\frac{50m}{60s}=\frac{5}{6}m/s$

Forholdet løpefart delt på svømmefart blir:

$\frac{v_l}{v_s}=\frac{5}{\frac{5}{6}}=6$

Han løper seks ganger raskere enn han svømmer, forholdet er 6:1.

Oppgave 19

a

Typetallet er den verdien det er mest av, karakter 4.

b

Fra karakter 1 ser vi at én elev utgjør 20 grader. Vi får:

$$\begin{gathered} 1:{40}^{\circ } \\ 2:{60}^{\circ } \\ 3:{60}^{\circ } \\ 4:{100}^{\circ } \\ 5:{80}^{\circ } \\ 6:{20}^{\circ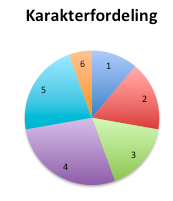 } \end{gathered}$$

c

Karaktersum: (1*2 + 2*3 + 3*3 + 4*5 + 5*4 + 6*1) = 63

Gjennomsnittskarakter: 63 : 18 = 3,5

Oppgave 20

300 km = 300 000 m = 30 000 000 cm

Siden 2 cm på kartet tilsvarer 30 millioner cm i virkeligheten er målestokken 2 : 30 000 000 som er 1 : 15 000 000.

Oppgave 21

Husk at areal av sirkel er $\pi r^2$ og overflaten av en sylinder (uten topp og bunn) er $h\cdot 2\pi r$

Overflate av sylinderen:

$$\begin{gathered} O=2\pi r^2+h\cdot 2\pi r \\ O\approx 2\cdot 3\cdot {10}^2+24\cdot 2\cdot 3\cdot 10 \\ O\approx 600+1440 \\ O\approx 2040 \end{gathered}$$

Alle mål i cm, så overflaten blir ca $2040c{m}^2$. (I virkeligheten er den noe større).

Del 2

Oppgave 1

a

De kjøper 880 euro til en stykkpris av 9,3165 NOK.

De betaler: $880\cdot 9,3165NOK=8198,52NOK$

b

Beløpet i norske kroner delt på antall euro gir oss kursen:

$\text{Math input error}$.

Oppgave 2

a

Hvert hjul har 10 siffer, du har altså 10 muligheter for hvert hjul:

${10}^4=10000$

Det er 10 000 kombinasjoner.

b

3377, 3737, 3773, 7337, 7373 og 7733.

c

Volum $V=l\cdot h\cdot b$

Dagens: $V=l\cdot h\cdot b=56cm\cdot 45cm\cdot 25cm=63000c{m}^3=63d{m}^3=63liter$

Fremtidens: $V=l\cdot h\cdot b=55cm\cdot 35cm\cdot 20cm=38500c{m}^3=38,5d{m}^3=38,5liter$

d

Fremtidens mål delt på dagens mål er 0,6111, det betyr at fremtidens volum er ca 61% av dagens, altså en reduksjon på ca 39%.

Oppgave 3

a

Kjørelengde: 287km + 83km + 371km = 741km

Bensinforbruk: $74,1mil\cdot 0,45liter/mil=33,35liter$

Bensinkostnad: $33,35\cdot 1,65=55,02$ Euro.

b

640€ er en fast utgift uavhengig av kjørelengde. Den variable kostnaden er 948€ - 640€ = 308€

De betaler 0,35€ per kilometer, altså

$$\begin{gathered} 308=0,35x \\ \frac{308}{0,35}=x \\ x=880 \end{gathered}$$

De kjørte 880 km

Oppgave 4

a

Pris og lønn i Euro.

b

Oppgave 5

a

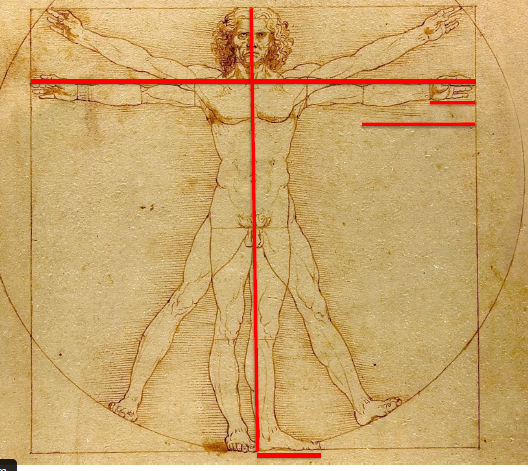
Forsvinningspunktet er i hodet på personen midt i bildet, trolig Jesus.

b

Måler med linjal og finner:

1. Høyde mann: 14cm - lengde fra fingertupp til fingertupp: 14cm. Påstanden er riktig.

2. Lengde av hånd delt på lengde av mann er 1/10. Målt: 1,5 cm og 14 cm, som gir 0,107 $\approx$0,11, altså ikke helt riktig. (størst usikkerhet i måling av hånd, desto kortere lengde, desto større prosentvis feil).

3. Høyde er 14 cm, og lengde albu - fingertupp er 3,6 cm. Det gir et forhold på 0,26, altså er påstanden feil.

4. Lengde fot er 2 cm, det gir et forhold 1/7 og påstanden er riktig.

Oppgave 6

a

h = 44,4m

$$\begin{gathered} h=4,9t^2 \\ t=\sqrt{\frac{44,4}{4,9}}=3,01\approx 3 \end{gathered}$$

Fallet tar ca. 3 sekunder.

b

Vi finner ut hvor kulen befinner seg etter to sekunder:

$h=4,9t^2=4,9\cdot 4=19,6$ meter under slippstedet.

44,4 meter - 19,6 meter = 24,8 meter.

Kulen faller altså ca. 25 meter det siste sekundet.

Oppgave 7

a

b

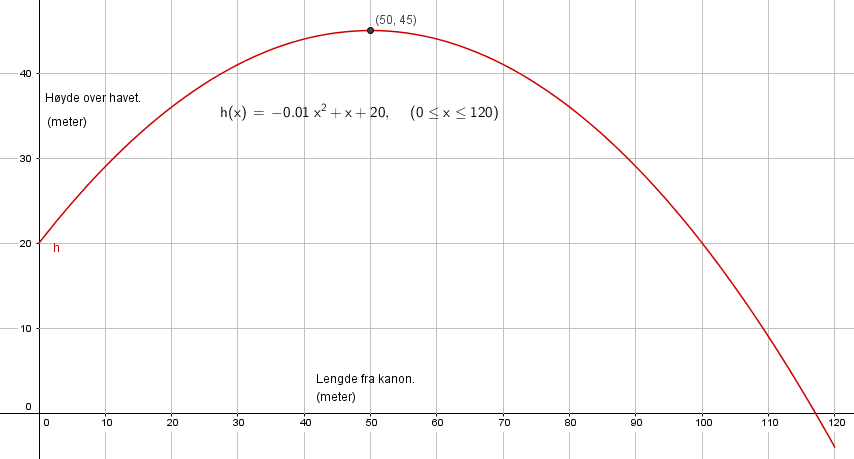
Bruker kommandoen "Ekstremalpunkt" i Geogebra og finner at maksimumshøyden er 45 meter når kula er 50 meter fra kanonen, i x - retning .

Oppgave 8

a

Fibonaccitall nr ni, ti elleve og tolv:

34, 55, 89 og 144.

b

De fire neste: 5a + 8b, 8a + 13b, 13a + 21b, 21a + 34b.

Oppgave 9

$$\begin{gathered} (40+r{)}^2={40}^2+(80-r{)}^2 \\ 1600+80r+r^2=1600+6400-160r+r^2 \\ 80r+160r=6400 \\ r=\frac{80}{3} \end{gathered}$$

Radius r i sirkelen er $\frac{80}{3}$ cm.