DEL 1

Oppgave 1

a)

$x^{2} - 3 x + 1 = 3 x + 8 x^{2} - 6 x - 7 = 0 x = \frac{6 \pm \sqrt{(- 6)^{2} - 4 \cdot (- 7)}}{2} x = \frac{6 \pm 8}{2} x_{1} = - 1 \lor x_{2} = 7$

b)

$l g (x^{4}) - l g (x^{3}) + l g (x^{2}) - l g x = 6 4 l g x - 3 l g x + 2 l g x - l g x = 6 2 l g x = 6 l g x = 3 x = 10^{3} x = 1000$

c)

$10 \cdot 4^{x} = 5 \cdot 2^{x} \frac{2^{2 x}}{2^{x}} = \frac{5}{10} 2^{2 x - x} = \frac{1}{2} 2^{x} = 2^{- 1} x = - 1$

Oppgave 2

a)

$(a + 2 b)^{2} - (2 b - a)^{2} = (a^{2} + 4 a b + 4 b^{2}) - (4 b^{2} - 4 a b + a^{2}) = a^{2} + 4 a b + 4 b^{2} - 4 b^{2} + 4 a b - a^{2} = 8 a b$

b)

$3^{3} \cdot 3^{0} + 3^{- 1} + 3^{- 2} + 3^{- 3} = 27 \cdot 1 + \frac{1}{3} + \frac{1}{3^{2}} + \frac{1}{3^{3}} = 27 + \frac{9}{27} + \frac{3}{27} + \frac{1}{27} = 27 + \frac{13}{27}$

Jeg synes dette svaret er penest, men man kan også skrive svaret slik:

$27 + \frac{13}{27} = \frac{729}{27} + \frac{13}{27} = \frac{742}{27}$

Oppgave 3

$x^{2} - 6 x \geq 7$

Løser likningen $x^{2} - 6 x - 7 = 0$ . Kjenner igjen denne likningen fra oppgave 1a). Løsningen er $x_{1} = - 1 \lor x_{2} = 7$

Et andregradsuttrykk $a x^{2} + b x + c$ med nullpunkter $x_{1}$ og $x_{2}$ kan faktoriseres slik: $a x^{2} + b x + c = a (x - x_{1}) (x - x_{2})$

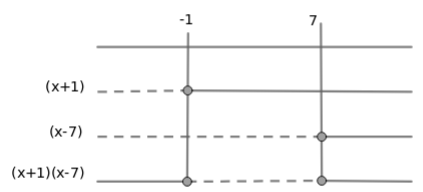
Faktoriserer andregradsfunksjonen: $x^{2} - 6 x - 7 = (x + 1) \cdot (x - 7)$

Lager fortegnsskjema:

Svar:

$x^{2} - 6 x \geq 7$ når $x \leq - 1 \lor x \geq 7$

Alternativt kan svaret skrives slik:

$x \in ⟨ \leftarrow, - 1] \cup [7, \to ⟩$

Velg din favoritt!

Oppgave 4

a)

b)

Bruker hypergeometrisk sannynlighet, og leser av binomialkoeffisientene i Pascals trekant. (Eksempel: $(\binom{7}{4})$ finner du i rad nr.7 og tall nr.4 i raden. Husk å begynne å telle på rad nr.0 og tall nr.0. Hvis du har talt riktig finner du at $(\binom{7}{4}) = 35$ ).

$P (2 J \cap 2 G) = \frac{(\binom{4}{2}) \cdot (\binom{3}{2})}{(\binom{7}{4})} = \frac{6 \cdot 3}{35} = \frac{18}{35}$

Sannsynligheten for at det blir trukket ut to jenter og to gutter er $\frac{18}{35}$

c)

P(minst en gutt) = 1 - P(ingen gutter) = $1 - \frac{(\binom{4}{4}) \cdot (\binom{3}{0})}{(\binom{7}{4})} = 1 - \frac{1 \cdot 1}{35} = \frac{35}{35} - \frac{1}{35} = \frac{34}{35}$

Sannsynligheten for at minst én gutt fra elevrådet blir med på turen er $\frac{34}{35}$

Oppgave 5

a)

$[\begin{array}{r} x + y = 1 \\ - 2 x + y = - 5 \end{array}]$

Trekker likning II fra likning I og får:

$x - (- 2 x) + (y - y) = 1 - (- 5) 3 x = 6 x = 2$

Setter inn $x = 2$ i likning I og får:

$2 + y = 1 y = - 1$

Løsning: $x = 2 \land y = - 1$

b)

Uttrykker de to første ulikhetene med hensyn på y:

Ulikhet nr. 1:

$x - 2 y \geq - 8 y \leq \frac{- x - 8}{- 2} y \leq \frac{x}{2} + 4$

NB: husk å snu ulikhetstegnet når du ganger eller deler en ulikhet med et negativt tall.

Ulikhet nr. 2:

$x + y \geq 1 y \geq - x + 1$

Vi har nå de tre ulikhetene:

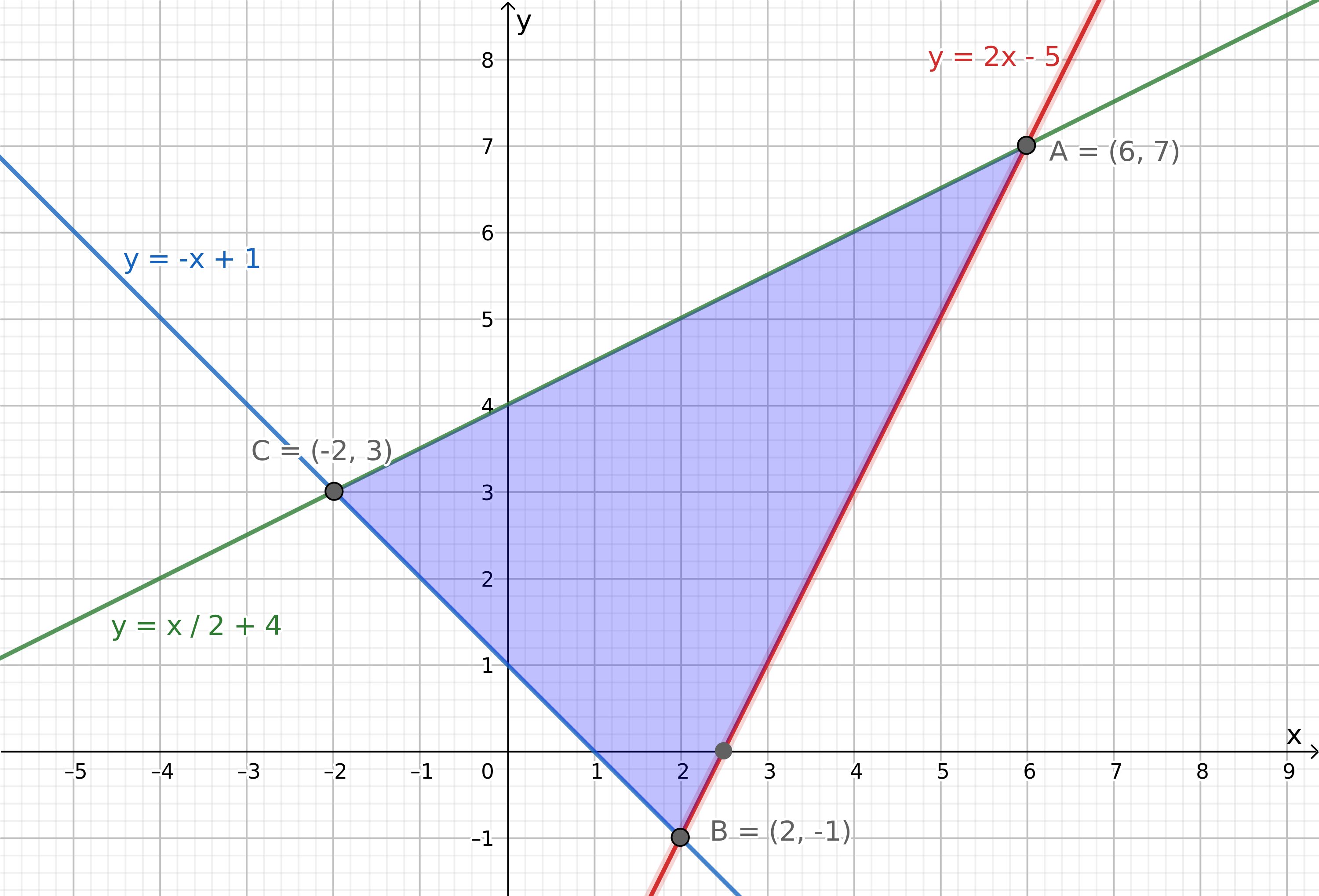
$y \leq \frac{x}{2} + 4 y \geq - x + 1 y \geq 2 x - 5$

Tegn de tre linjene $y = \frac{x}{2} + 4, y = - x + 1, y = 2 x - 5$ (for hånd siden det er del 1). Legg godt merke til hvilken vei ulikhetstegnet er i de fire ulikhetene, og skraver området som avgrenses av disse.

c)

Sjekker verdien til $3 x - y$ i punkt A,B og C.

Punkt A: $3 \cdot 6 - 7 = 11$

Punkt B: $3 \cdot 2 - (- 1) = 7$

Punkt C: $3 \cdot (- 2) - 3 = - 9$

Størrelsen $3 x - y$ har størst verdi i punktet (6,7). Da er verdien 11.

Oppgave 6)

a)

$O (x) = - 0, 25 x^{2} + 10 x - 75 O^{'} (x) = - 0, 5 x + 10$

Setter $O^{'} (x) = 0$

$- 0, 5 x + 10 = 0 - 0, 5 x = - 10 x = 20$

Den produksjonsmengden som gir størst overskudd er 20 enheter per dag. Finner overskuddet $O (20)$

$O (20) = - 0, 25 \cdot 20^{2} + 10 \cdot 20 - 75 = - 0, 25 \cdot 400 + 200 - 75 = - 100 + 200 - 75 = 25$

Overskuddet blir 25 000 kr.

S1 2018 høst LØSNING