R2 2012 høst LØSNING

Del 1

Oppgave 1

a)

$f(x)=e^x\cos x$

Produktregelen for derivasjon gir at

$f^{\prime }(x)=e^x\cos x-e^x\sin x=e^x(\cos x-\sin x)$

b)

$g(x)=5(1+\sin x{)}^3$

Potensregelen og kjerneregelen for derivasjon gir at

$g^{\prime }(x)=15(1+\sin x{)}^2\cdot \cos x$

Oppgave 2

a)

$\int \cos x\cdot (1+\sin x{)}^{3}dx$

La $u=\sin x$. Da er $du=\cos xdx$. Integralet blir dermed

$\int (1+u{)}^{3}du=\frac{1}{4}(1+u{)}^4+C=\frac{1}{4}(1+\sin x{)}^4+C$, der $C$ er en integrasjonskonstant.

b)

${\int }_1^{e}x\ln xdx$

Vi bruker delvis integrasjon. Det gir

${\int }_1^{e}x\ln xdx=[\frac{1}{2}{x}^2\ln x{]}_1^e-{\int }_1^e\frac{1}{2}xdx=\frac{1}{2}{e}^2-\frac{1}{4}[x^2{]}_1^e=\frac{1}{4}{e}^2+\frac{1}{4}$

Oppgave 3

a)

Vi har gitt punktene $A(1,1,1)$, $B(2,1,5)$ og $C(3,7,3)$, som vi betrakter som vektorer. Da er sidene i $\mathrm{△}ABC$

$B-A=(2,1,5)-(1,1,1)=(1,0,4)$, $C-A=(3,7,3)-(1,1,1)=(2,6,2)$ og $C-B=(3,7,3)-(2,1,5)=(1,6,-2)$.

Siden prikkproduktene mellom hvert par av sider (betraktet som vektorer) er ulik $0$, er ingen av vinklene rette, altså er ikke trekanten rettvinklet.

b)

Koordinatet til punktet $D$ er ikke entydig bestemt siden det er flere måter å utvide trekanten til et parallellogram.

Vi kan f.eks. la $D$ være gitt som $A+(B-A)+(C-A)=(1,1,1)+(1,0,4)+(2,6,2)=(4,7,7)$. Altså får vi koordinatet $D(4,7,7)$

Oppgave 4

a)

Vi har gitt ligningen $y^{\prime \prime }-y=0$.

Karakteristisk ligning blir derfor ${\lambda }^2=1$, med løsninger $\lambda =\pm 1$. Løsningen blir derfor

$y=C_1{e}^x+C_2{e}^{-x}$.

b)

Initialverdiene $y(0)=5$ og $y^{\prime }(0)=-1$ er gitt. Setter vi disse inn i løsningen fra forrige deloppgave får vi

$$\begin{gathered} y(0)=C_1+C_2=5 \\ {y}^{\prime }(0)=C_1-C_2=-1 \end{gathered}$$

Legger vi sammen de to ligningene får vi

$2C_1=4$, så $C_1=2$. Da er $C_2=5-C_1=5-2=3$.

Oppgave 5

Vi har gitt den uendelige rekken $1+\frac{1}{3}+\frac{1}{9}+\frac{1}{27}+\cdots$.

Den kan skrives som $\sum _{n=0}^{\mathrm{\infty }}(\frac{1}{3}{)}^n$, som vi gjenkjenner som en geometrisk rekke.

Det er kjent at geometriske rekker $\sum _{n=0}^{\mathrm{\infty }}{r}^n$ konvergerer dersom $|r|<1$. Siden $\frac{1}{3}<1$ vil rekken konvergere.

Formelen for geometriske rekker er $\sum _{n=0}^{\mathrm{\infty }}{r}^n=\frac{1}{1-r}$. Altså er

$\sum _{n=0}^{\mathrm{\infty }}(\frac{1}{3}{)}^n=\frac{1}{1-\frac{1}{3}}=\frac{3}{2}$

Oppgave 6

Vi har gitt den periodiske funksjonen $f(x)=a\sin (cx+\phi )+d$. Vi kan uten tap av generalitet anta at $a>0$: For $a<0$ kan vi redefinere konstanten til $-a$ og flytte $-1$ innenfor $\sin$.

For å finne $c$ legger vi merke til at $5c+\phi -(3c+\phi )=\pi$, altså er $c=\frac{\pi }{2}$. Videre er $\frac{5\pi }{2}+\phi =\frac{\pi }{2}$, altså er $\phi =-2\pi$, men siden $\sin (x+2\pi )=\sin x$ kan vi like gjerne velge $\phi =0$.

For å finne $a$ og $d$, legger vi nå merke til at $f(0)=5=d$. I toppunktet er til slutt $f(5)=a+5=8$, så $a=3$.

Funksjonen blir derfor $f(x)=3\sin (\frac{\pi }{2}x)+5$.

Oppgave 7

a)

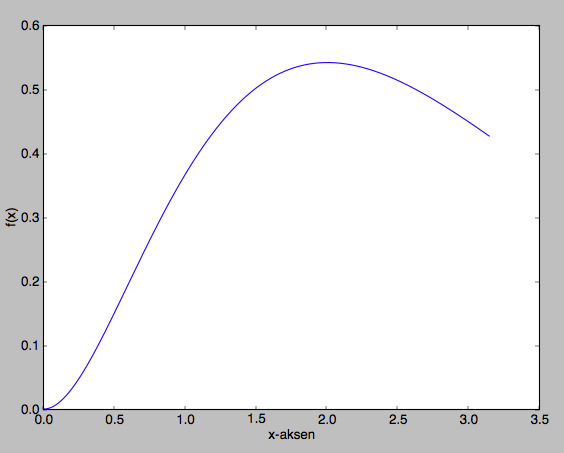
Funksjonen $f(x)=x^2{e}^{-x}$ er gitt. Topp- og bunnpunkt er bestemt ved å løse $f^{\prime }(x)=0$. Vi har at $f^{\prime }(x)=2x{e}^{-x}-x^2{e}^{-x}=0$, altså er $x(2-x)=0$ som gir at $x=0$ eller $x=2$. Fra grafen i deloppgaven under ser vi at $x=2$ er et toppunkt og $x=0$ et bunnpunkt.

b)

Oppgave 8

Vi har gitt formelen $\sum _{i=1}^{n}i(i+3)=\frac{n(n+1)(n+5)}{3}$ som skal bevises med induksjon.

Først ser vi at formelen er riktig for $n=1$, siden $1\cdot (1+3)=4=\frac{1\cdot 2\cdot 6}{3}$

Anta at formelen er riktig for en bestemt $n$. Vi legger til neste ledd av summen på hver side og får

$\sum _{i=1}^{n+1}i(i+3)=\frac{n(n+1)(n+5)}{3}+(n+1)(n+4)=\frac{(n+1)(n(n+5)+3(n+4))}{3}=\frac{(n+1)(n^2+8n+12)}{3}$.

Siden $(n+2)(n+6)=n^2+8n+12$, ser vi at $\frac{(n+1)(n^2+8n+12)}{3}=\frac{(n+1(n+2)(n+6)}{3}$. Altså er

$\sum _{i=1}^{n+1}i(i+3)=\frac{(n+1(n+2)(n+6)}{3}$, så formelen er riktig for $n+1$. Altså er formelen riktig for alle positive heltall $n$.

Del 2

Oppgave 1

a)

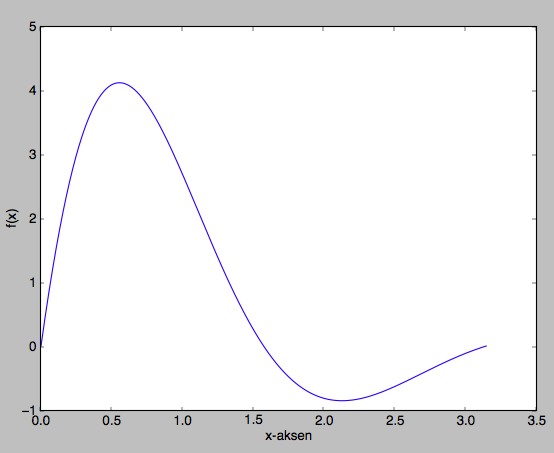
Nullpunkt finnes ved å løse $8e^{-x}\sin 2x=0$. Siden eksponensialfunksjonen er positiv overalt er der nok å betrakte $\sin 2x=0$, som er tilfelle når $x=\frac{\pi }{2}$.

Topp- og bunnpunkt finner vi ved å løse $f^{\prime }(x)=0$. Vi har at $f^{\prime }(x)=-8e^{-x}\sin 2x+16e^{-x}\cos 2x=0$. Altså $2\cos 2x=\sin 2x$. Dette er det samme som at $\tan 2x=2$ eller $x=\frac{1}{2}(\pi n+\arctan 2)$ for heltall $n$. Fra grafen ser vi at $x=\frac{1}{2}\arctan 2\approx 0.55$ svarer til toppunktet, mens $x=\frac{1}{2}(\pi +\arctan 2)\approx 2.12$ svarer til bunnpunktet.

Oppgave 2

a)

Diff.ligningen $v^{\prime }=12.0-1.15v$ er gitt. Dette er en separabel ligning som kan skrives ${\int }_0^{v(t)}\frac{dv}{12.0-1.15v}={\int }_0^{t}ds$. Utfører vi integrasjonene får vi at dette blir $\frac{1}{-1.15}[\ln (12.0-1.15v){]}_0^{v(t)}=t$. $\ln (\frac{12.0-1.15v(t)}{12.0})=-1.15t$, som er det samme som $1-\frac{1.15}{12.0}v(t)=e^{-1.15t}$. Isolerer vi $v(t)$ får vi nå at $v(t)=\frac{12.0}{1.15}(1-e^{-1.15t})$. Løsningen verifiseres ved innsetting i diff.ligningen.

b)

Siden $s^{\prime }(t)=v(t)$, er $s(t)={\int }_0^{t}v(s)ds={\int }_0^t\frac{12.0}{1.15}(1-e^{-1.15s})ds=[\frac{12.0}{1.15}(s+\frac{1}{1.15}{e}^{-1.15s}){]}_0^t=\frac{12.0}{1.15}(t+\frac{1}{1.15}(e^{-1.15t}-1))$

c)

Vi må løse ligningen $100=s(t)=\frac{12.0}{1.15}(t+\frac{1}{1.15}(e^{-1.15t}-1))$. Vi kan omskrive denne til $\frac{115}{12}=t+\frac{1}{1.15}(e^{-1.15t}-1)$. Denne ligningen er vanskelig å løse analytisk, så vi må benytte numeriske metoder. Vi kan f.eks. finne det positive nullpunktet til funksjonen $f(t)=t+\frac{1}{1.15}(e^{-1.15t}-1)-\frac{115}{12}$ med kalkulatoren. Plotter vi funksjonen finner vi at nullpunktet er $\approx 10.45$. Dette virker realistisk når vi sammenligner med 100m-tidene på internasjonalt nivå.

Oppgave 3

a)

1)

Dersom $\overrightarrow{a}\cdot \overrightarrow{b}=0$ må $\overrightarrow{a}$ og $\overrightarrow{b}$ stå vinkelrett på hverandre.

2)

Dersom $\overrightarrow{a}\times \overrightarrow{b}=0$ må $\overrightarrow{a}$ og $\overrightarrow{b}$ være parallelle.

3)

Dersom $\overrightarrow{a}\cdot (\overrightarrow{b}\times \overrightarrow{c})=0$ må enten $\overrightarrow{a}$ og $\overrightarrow{b}\times \overrightarrow{c}$ stå vinkelrett på hverandre, eller $\overrightarrow{b}$ og $\overrightarrow{c}$ være parallelle.

b)

Vi har at $(\overrightarrow{a}\times \overrightarrow{b}{)}^2=|\overrightarrow{a}{|}^2|\overrightarrow{b}{|}^2{\sin }^2\theta$ og $\overrightarrow{a}\cdot \overrightarrow{b}=|\overrightarrow{a}||\overrightarrow{b}|\cos \theta$. Altså er $(\overrightarrow{a}\times \overrightarrow{b}{)}^2+(\overrightarrow{a}\cdot \overrightarrow{b}{)}^2=|\overrightarrow{a}{|}^2|\overrightarrow{b}{|}^2{\sin }^2\theta +|\overrightarrow{a}{|}^2|\overrightarrow{b}{|}^2{\cos }^2\theta =|\overrightarrow{a}{|}^2|\overrightarrow{b}{|}^2({\sin }^2\theta +{\cos }^2\theta )=|\overrightarrow{a}{|}^2|\overrightarrow{b}{|}^2$

c)

Arealet av trekanten er $A=|\overrightarrow{a}\times \overrightarrow{b}|=\sqrt{(\overrightarrow{a}\times \overrightarrow{b}{)}^2}=\sqrt{|\overrightarrow{a}{|}^2|\overrightarrow{b}{|}^2-(\overrightarrow{a}\cdot \overrightarrow{b}{)}^2}$, der vi har brukt formelen fra forrige deloppgave.

Dersom $\overrightarrow{a}\cdot \overrightarrow{b}=0$ er vektorene $\overrightarrow{a}$ og $\overrightarrow{b}$ vinkelrette. Da er trekanten rettvinklet, så arealet blir $\frac{1}{2}|\overrightarrow{a}||\overrightarrow{b}|$. Dersom $\overrightarrow{a}\times \overrightarrow{b}=0$ må $\overrightarrow{a}$ og $\overrightarrow{b}$ være parallelle, så trekanten er degenerert, dvs. at to av hjørnene ligger på en linje, så arealet er $0$.

d)

Vi har at $\overrightarrow{a}=[2,3,4]-[1,1,1]=[1,2,3]$ og $\overrightarrow{b}=[3,1,5]-[1,1,1]=[2,0,4]$. Da er $\overrightarrow{a}\cdot \overrightarrow{b}=[1,2,3]\cdot [2,0,4]=2+12=14$, $|\overrightarrow{a}|=\sqrt{1+4+9}=\sqrt{14}$ og $|\overrightarrow{b}|=\sqrt{4+16}=\sqrt{20}$.

Arealformelen fra forrige deloppgave gir nå at $A=\frac{1}{2}\sqrt{14\cdot 20-{14}^2}=\frac{1}{2}\sqrt{84}=\sqrt{21}$

Oppgave 4

a)

Rekken $1+3+5+\cdots +(2n-1)$ har $n$ ledd med gjennomsnitt $\frac{2n-1+1}{2}=n$. Altså er summen $S_n=n^2$. For at $S_n=n^2=1600$, må $n=\sqrt{1600}=40$.

b)

Rekken kan skrives som $\sum _{i=0}^{\mathrm{\infty }}(\frac{1}{4}{)}^i$, altså en geometrisk rekke. Siden $|\frac{1}{4}|<1$ er rekken konvergent, og konvergerer mot $\frac{1}{1-\frac{1}{4}}=\frac{4}{3}$.

Oppgave 5

a)

Ellipsen $(\frac{x}{a}{)}^2+(\frac{y}{b}{)}^2=1$ er gitt. Vi flytter over det første leddet og ganger hele ligningen med $b^2$ og får $y^2=b^2-\frac{b^2{x}^2}{a^2}$

b)

Volumet av rotasjonslegemet er ${\int }_{-a}^a\pi y^{2}dx=\pi {\int }_{-a}^a{b}^2-\frac{b^2{x}^2}{a^2}dx=2a{b}^2\pi -\frac{\pi b^2}{3a^2}[x^3{]}_{-a}^a=\frac{4}{3}\pi a{b}^2$

Oppgave 6

a)

Ligningen til en tangent er generelt $y=\alpha x+\beta$. Stigningstallet $\alpha =f^{\prime }(a)=\frac{1}{2\sqrt{a-2}}$ Tangenten må gå gjennom punktet $P(a,f(a))=(a,\sqrt{a-2})$, så $\sqrt{a-2}=\frac{a}{2\sqrt{a-2}}+\beta$, altså er $\beta =\sqrt{a-2}-\frac{a}{2\sqrt{a-2}}=\frac{a-4}{2\sqrt{a-2}}$.

Punktet $A$ er bestemt av at tangentlinjen skjærer x-aksen, altså må $y=0$ i $A$. Setter vi inn $y=0$ i ligningen for tangenten får vi x-koordinaten til $A$. Vi får $0=\frac{x}{2\sqrt{a-2}}+\frac{a-4}{2\sqrt{a-2}}$, altså er $x=4-a$. Så $A(4-a,0)$. Videre er $B(x,f(x))$ der $f(x)=0$, altså må $\sqrt{x-2}=0$, som gir at $x=2$. Derfor er $B(2,0)$. Til slutt er $C(a,0)$.

b)

${\int }_2^a\sqrt{x-2}dx=[\frac{2}{3}(x-2{)}^{\frac{3}{2}}{]}_2^a=\frac{2}{3}(a-2{)}^{\frac{3}{2}}$.
Arealet av $\mathrm{△}ACP$ er $A=\frac{1}{2}f(a)(a-(4-a))=\sqrt{a-2}(a-2)=(a-2{)}^{\frac{3}{2}}$

c)

Dette er åpenbart fra de beregningene vi har gjort i forrige deloppgave. Arealet til trekanten er $(a-2{)}^{\frac{3}{2}}$. Området under grafen til $f$ er $\frac{2}{3}(a-2{)}^{\frac{3}{2}}$, så arealet av det andre området innenfor trekanten er $(a-2{)}^{\frac{3}{2}}-\frac{2}{3}(a-2{)}^{\frac{3}{2}}=\frac{1}{3}(a-2{)}^{\frac{3}{2}}$. Altså er området under grafen dobbelt så stort som det andre området.