Likninger
Her vil du finne en oversikt over de typer likninger som behandles på matematikk.net.
Likninger med en ukjent (1. grad)
Innledning
I matematikk er det vanlig å bruke bokstaver som erstatning for tallverdier. Bokstaver kan symbolisere tall som vi kjenner, for eksempel π som har tallverdi 3,14. Bokstavene kan også symbolisere tallverdier som vi ikke kjenner, men som vi ønsker å finne. I slike tilfeller bruker vi gjerne bokstavene x, y eller z.
I et spesielt regnestykke kan x kun ha en tallverdi, men x kan ha forskjellige verdier i forskjellige regnestykker.
La oss se på noen eksempler:
Per og Kari har til sammen 5 epler. Per har to. Hvor mange har Kari?
Dette stykket greier du sikkert i hodet, men la oss sette det opp som en ligning slik at vi lærer oss tenkemåten. La oss kalle antall epler som Kari har for x.
Per + Kari = tilsammen
2 + ? = 5
Som likning kan dette skrives:
2 + x = 5
Tenk på en skålvekt. En skålvekt er i likevekt dersom lasten er den samme i begge skålene. Vi kan legge på mer last på vekten, men for at den skal være i likevekt må vi legge like mye i begge skålene. Vi kan også fjerne last fra skålvekten, men vi må fjerne like mye fra begge skålene for at likevekten skal holde seg. Gjør vi ikke det kommer vekten ut av balanse.
Tenk deg at likhetstegnet i vår ligning er balansepunket på skålvekten. Vi kan legge til og trekke fra på begge sider, vi kan gange og dele, men det er viktig at vi gjør det samme på begge sider av likhetstegnet. Gjør vi ikke det kommer "vekten" ut av balanse.
Situasjonen med Per og Kari ser slik ut:

Karis epler befinner seg i sekken. Vår oppgave er å finne antall epler i sekken, x.
Dersom vi fjerner to epler på hver side av skålvekten ser det slik ut:
På matematikkspråk kan vi skrive det slik:
2 + x = 5
Dersom vi trekker bort to fra hver side av likhetstegnet får vi:
2 + x - 2 = 5 - 2
x = 5 - 2
"flytt og bytt" er en huskeregel, men det er viktig å forstå at man trekker fra samme tall på begge sider av likhetstegnet.
Med "flytt og bytt" mener man at man flytter leddet som ikke inneholder x over på høyre side av likhetstegnet og bytter fortegn. Likedan kan man flytte ledd som inneholder x fra høyre til venstre side av likhetstegnet og skifte fortegn. Det man i virkeligheten gjør er å trekke fra like mange på hver side.
Når vi løser en ligning er det vår oppgave å få x alene på venstre side av likhetstegnet.
Omvendte operasjoner
- Addisjon og subtraksjon opphever hverandre.
- Multiplikasjon og divisjon opphever hverandre.
- Operasjonene må utføres på alle ledd i likningen, på begge sider av likhetstegnet.
$5$ x $ =25 + 25$
Ligning med x som ledd
Man flytter alle ledd med x på venstre side og alle ledd uten x på høyre side av likhetstegnet. Husk å bytt fortegn på de ledd som flyttes. Trekk sammen på begge sider av likhetstegnet.
Eksempel 1:
<math> x = 2 </math>
Ligning med x som faktor
Løsningen er å dividere alle ledd på begge sider av likhetstegnet med tallet som står foran x.
Eksempel 2:
<math>5x = x + 8 \quad \quad</math> Flytter over x på venstre side og skifter fortegn.
<math> 5x - x = 8 \quad \quad</math> Trekker sammen
<math> 4x = 8 \quad|:4 \quad \quad</math>Deler begge sider av likhetstegnet på det tallet som står forran x, i dette tilfelle 4.
<math> x = 2 </math>
Ligninger med x i teller
Løsningen er å multiplisere alle ledd på begge sider av likhetstegnet med tallet i nevner.
Eksempel 1:
Ligninger med x i nevner
Løsningen er å multiplisere alle ledd på begge sider av likhetstegnet med x.
Eksempel 1:
<math> x = 1 </math>
Kombinasjoner av metoder
Ofte vil ligningene du løser være en kombinasjon av metodene over:
Eksempel 2:
<math> x = \frac12 </math>
Prøve på Svaret
Hvordan kan vi være sikre på at utregningene i eksemplet over er riktige? Et godt hjelpemiddel er å sette prøve på svaret. Det betyr at vi setter inn den x verdien vi har funnet i ligningen. Vi behandle hver side av likhetstegnet for seg. Dersom svaret vi får blir det samme på begge sider av likhetstegnet har vi med stor sannsynlighet regnet riktig.
Vi tester svaret over:
Eksempel
<math>VS: \qquad \qquad 3 \cdot \frac12 + \frac{\frac12}{2} = \frac32 + \frac 14 = \frac 74 </math>
<math>HS:\qquad \qquad 4 - \frac{2}{\frac12} + \frac{7\cdot \frac12}{2}= 4 - 4 + \frac74 = \frac74</math>
Vi ser at vi får det samme på begge sider og kan konkludere med at x verdien vi fant er riktig.
Gjør det til en regel at du setter prøve på svaret, selv om det ikke alltid spørres etter det.
Dagligdags Bruk - tekststykker
Når du har lært regnereglene blir utfordringen å omforme dagligdagse problemer til ligninger. Dette er et meget slagkraftig redskap, når du lærer å bruke det:
Eksempel 1:
Astrid er halvparten så gammel som Thorild. Knut er tre år eldre enn Thorild. Til sammen er de 53 år gamle. Hvor gammel er Astrid, Thorild og Knut?
Løsning:
Vi kaller alderen til Thorild for <math>x.</math>
Knut er: <math>x+3</math>
Når man legger sammen alderen til de tre, får følgende likning:
<math> \frac x2 + x + (x+3)=53</math>
<math> 2,5x =50</math>
<math> x =20</math>
Siden x er 20 betyr det at Thorild er 20 år, Astrid er 10 år og Knut 23 år gammel.
Operasjonenesrekkefølge
Dersom man har en ligning med både brøk og parentes kan den løses etter følgende oppskrift:
- multipliser ut parentesene
- sett parenteser rundt brøker med negative fortegn, dersom de har flere ledd i teller
- fjern brøkene ved å multiplisere alle ledd på begge sider av likhetstegnet med minste felles multiplum
- flytt og bytt slik at alle x ledd kommer på venstre side og alle ledd uten x på høyre side trekk sammen
- divider begge sider på koeffisienten foran x
Likningsett med to ukjente
Andregradslikninger
Innledning
Fra siden om potenser uten brøkeksponent vet vi at $x \cdot x = x^2$. Sagt med ord sier vi at "$x$ multiplisert med seg selv er lik $x$ i andre".
Andregradslikninger inneholder alltid et ledd hvor $x^2$ er en faktor.
En andregradslikning er en likning på formen $ax^2 + bx + c = 0$, der $a$, $b$ og $c$ er konstanter og $a \neq 0$. Konstantene i en annengradslikning kalles koeffisienter.
En løsninger av en likning kalles også en rot i likningen. Å finne røttene i en likning er altså det samme som å løse likningen.
En fullstendig andregradslikning skrives på formen
- <math>
\displaystyle ax^2 + bx + c = 0 </math>
Likningen har tre ledd:
- <math> ax^2 </math> kalles andregradsleddet,
- <math> bx </math> kalles førstegradsleddet,
- <math> c </math> kalles konstantleddet.
Ufullstendig likninger
Dersom minst en av koeffisientene $b$ eller $c$ er lik null sier vi at andregradslikningen er ufullstendig. Dette er spesialtilfeller av andregradslikninger, fordi én av koeffisientene er lik null, slik at likningene mangler et ledd.
Dersom $a = 0$ har vi en førstegradslikning som løses med metoden beskrevet i likninger av første grad.
Tilfellet b = 0
Dersom $b = 0$ ser likningen slik ut:
- <math>
\displaystyle ax^2 + c = 0 </math>
Denne løses med "bytt og flytt", for så å ta kvadratrot:
- <math>
\begin{aligned} x = \pm \sqrt {- \frac {c}{a}} \end{aligned} </math>
Legg merke til at enten $a$ eller $c$ (men ikke begge!) må være negativ for at denne likningen skal ha en løsning. Vi kan ikke ta kvadratroten av et negativt tall.
Eksempel:
Løs likningen
- <math>
\displaystyle 4x^2 - 8 = 0 </math>
Vi løser ved "bytt og flytt" og deretter ta kvadratroten:
- <math>
\begin{aligned} 4x^2 &= 8 \\ x^2 &= \frac84 \\ x &= \pm \sqrt { \frac {8}{4}} \end{aligned} </math>
- <math>
\displaystyle x = \sqrt {2} \qquad \vee \qquad x = - \sqrt {2} </math>
Tilfellet c = 0
Dersom $c = 0$ har vi følgende formel:
- <math>
\displaystyle ax^2 + bx = 0 </math>
Vi løser ved faktorisering:
- <math>
\displaystyle x (ax + b) = 0 </math>
- <math>
\begin{aligned} x = 0 \qquad &\vee \qquad ax + b = 0 \\ x = 0 \qquad &\vee \qquad x = - \frac ba \end{aligned} </math>
Eksempel:
Løs likningen
- <math>
\displaystyle -3x^2 + 6x = 0 </math>
Løsning ved faktorisering:
- <math>
\displaystyle x (-3x + 6) = 0 </math>
- <math>
\begin{aligned} x = 0 \qquad &\vee \qquad -3x + 6 = 0 \\ x = 0 \qquad &\vee \qquad x = 2 \end{aligned} </math>
ABC-formelen
En andregradslikning på formen $ax^2 + bx + c =0$ kan alltid løses ved hjelp av ABC-formelen, som ser slik ut:
ABC-formelen er
- <math>
\displaystyle x= \frac{-b \pm \sqrt{b^2-4ac}}{2a} </math>
når
- <math>
\displaystyle ax^2 + bx + c =0 </math>
Dersom $b^2-4ac$ er positiv, vil likningen ha to ulike løsninger. Dersom $b^2-4ac = 0$ kan vi si at likningen har en enkelt løsning - eller også to like løsninger.
$a$, $b$ og $c$ er koeffisientene i andregradsuttrykket. Legg merke til at dersom $b^2 - 4ac$ er mindre enn null, får man et negativt tall under rottegnet. Man sier da at likningen ikke har reelle løsninger.
(I høyere kurs viser man at likningen kan ha komplekse løsninger).
Eksempel 1:
Løs likningen
- <math>
\displaystyle 3x^2 + 2x - 1 =0 </math>
Likningen har koeffisenter $a = 3$ , $b = 2$ og $c = -1.$
Ved å bruke ABC-formelen får man:
- <math>
\begin{aligned} x &= \frac{-2 \pm \sqrt{2^2-4 \cdot 3 \cdot (-1)}}{2 \cdot 3} \\ \\ &= \frac{-2 \pm \sqrt{4+12}}{6} \\ \\ &= \frac{-2 \pm 4}{6} \end{aligned} </math>
Likningen har to ulike løsninger:
- <math>
\begin{aligned} x = \frac{-2 + 4}{6} \qquad &\vee \qquad x= \frac{-2 - 4}{6} \\ \\ x = \frac{1}{3} \qquad &\vee \qquad x = - 1 \end{aligned} </math>
Eksempel 2:
Finn røttene i likningen
- <math>
\displaystyle -x^2 + 4x - 4 =0 </math>
Koeffisientene er $a = -1$ , $b = 4$ og $c = -4.$
Ved å bruke ABC-formelen får man:
- <math>
\begin{aligned} x &= \frac{-4 \pm \sqrt{4^2-4 \cdot (-1) \cdot (-4)}}{2 \cdot (-1)} \\ \\ &= \frac{-4 \pm \sqrt{16-16}}{-2} \end{aligned} </math>
Med null under rottegnet får man kun en løsning, $x = 2$.
Eksempel 3:
Løs likningen:
- <math>
\displaystyle 3x^2 + 2x + 2 =0 </math>
Koeffisientene er $a = 1$ , $b = -2$ og $c = 2$.
Ved å bruke ABC-formelen får man:
- <math>
\begin{aligned} x &= \frac{2 \pm \sqrt{(-2)^2-4 \cdot 1 \cdot 2}}{2 \cdot 1} \\ \\ &= \frac{2 \pm \sqrt{4-8}}{2} \\ \\ &= \frac{2 \pm \sqrt{-4}}{2} \end{aligned} </math>
Her ser man et man får et negativt tall under rottegnet. Da er det på tide å stoppe opp og konkludere med at likningen ikke har reell løsning.
Eksempel 4:
Løs likningen:
- <math>
\displaystyle 4x^2 - 1 =0 </math>
Koeffisientene er $a = 4$ , $b = 0$ og $c = -1.$
Likningen mangler førstegradsleddet ($b = 0$), og det enkleste i dette eksempelet er å bruke "bytt og flytt" og så ta kvadratroten, som vist over. Det er også fullt mulig å bruke ABC-formelen, og da får man:
- <math>
\begin{aligned} x &= \frac{ \pm \sqrt{-4 \cdot 4 \cdot (-1)}}{2 \cdot 4} \\ \\ &= \frac{ \pm \sqrt{16}}{8} \\ \\ &=\pm \frac{ 4}{8} \end{aligned} </math>
Likningen har to løsninger:
- <math>
\displaystyle x= \frac{1}{2} \qquad \vee \qquad x= - \frac{1}{2} </math>
Eksempel 5:
Løs likningen:
- <math>
\displaystyle -3x^2 + 6x = 0 </math>
Koeffisentene er $a = -3$ , $b = 6$ og $c = 0.$
Ved å bruke ABC-formelen får man:
- <math>
\begin{aligned} x &= \frac{-6 \pm \sqrt{6^2}}{-6} \\ \\ &= \frac{-6 \pm 6}{-6} \end{aligned} </math>
- <math>
\displaystyle x= 2 \qquad \vee \qquad x= 0 </math>
Man ser at ABC-formelen virker her også, men siden konstantleddet mangler ($c = 0$), ville det være mer fornuftig å faktorisere ut $x$ og løse likningene som vist over.
Grafisk fremstilling av andregradslikninger
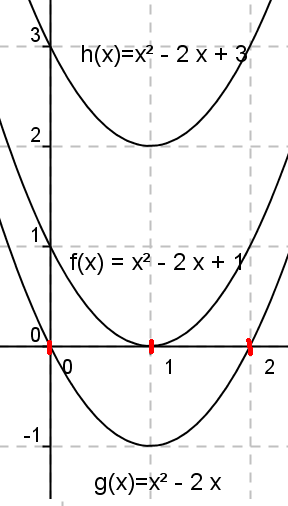
Hvorfor har noen likninger to løsninger, noen en og andre ingen? Det kan vi forstå dersom vi studerer grafen til andregradspolynomet i likningen. Løsninger i likningen finner vi som verdiene av $x$ der grafen skjærer $x$-aksen, det vil si der $y = 0$.
Figuren under viser tre ulike andregradspolynom.
Dersom grafen til andregradspolynomet krysser $x$-aksen, har likningen to løsninger. Likningen $g(x) = 0$ har to løsninger fordi $b^2-4ac>0$, og grafen til $g(x)$ skjærer $x$-aksen to steder.
Dersom grafen tangerer $x$-aksen har likningen en løsning. Likningen $f(x) = 0$ har en løsning fordi $b^2-4ac=0$. Grafen til $f(x)$ tangerer $x$-aksen i ett punkt, i $x= \frac{-b}{2a}$.
Dersom grafen til polynomet ikke krysser eller tangerer $x$-aksen, har likningen ingen løsning. Likningen $h(x) =0$ har ingen løsning fordi $b^2-4ac<0$. Man kan ikke ta kvadratroten av et negativt tall.
Bevis for ABC-formelen
For å bevise ABC-formelen bruker en første kvadratsetning, som vist i det følgende avsnittet.
- <math>
\begin{aligned} ax^2 + bx + c &= 0 \\ \\ x^2 + \frac bax + \frac ca &= 0 \\ \\ x^2 + \frac bax &= - \frac ca \\ \\ x^2 + 2\frac {b}{2a}x &= - \frac ca \\ \\ x^2 + 2\frac {b}{2a}x + (\frac {b}{2a})^2 &= - \frac ca + (\frac {b}{2a})^2 \\ \\ (x +\frac {b}{2a})^2 &= - \frac ca + \frac {b^2}{4a^2} \\ \\ (x +\frac {b}{2a})^2 &= - \frac {4ac}{4a a} + \frac {b^2}{4a^2} \\ \\ (x +\frac {b}{2a})^2 &= \frac {-4ac+b^2}{4a^2} \\ \\ (x +\frac {b}{2a}) &= \pm \sqrt{\frac {b^2 -4ac}{4a^2}} \\ \\ x &= -\frac {b}{2a} \pm {\frac {\sqrt {b^2 -4ac}}{2a}} \\ \\ x &= \frac{-b \pm \sqrt{b^2-4ac}}{2a} \end{aligned} </math>
Fullstendig kvadrat
Man kan bygge opp et fullstendig kvadrat ved å halvere, kvadrere, addere.....
For å kunne bruke teknikken må du kunne kvadratsetningene godt.
Det følgende eksempelet viser hvordan det gjøres:
Eksempel:
Løs likningen
- <math>
\displaystyle 2x^2 - 3x +1 = 0 </math>
Vi omformer likningen:
- <math>
\begin{aligned} x^2 - \frac 32 x + \frac 12 &=0 \\ \\ x^2 - \frac 32 x &= - \frac 12 \\ \\ x^2 - \frac 32 x &= - \frac 12 \\ \\ x^2 - \frac 32 x + ( \frac 34)^2 &= - \frac 12 + ( \frac 34)^2 \\ \\ (x - \frac 34)^2 &= \frac {1}{16} \end{aligned} </math>
- <math>
\begin{aligned} x - \frac 34 = \sqrt{ \frac {1}{16}}\qquad &\vee \qquad x - \frac 34 = -\sqrt{ \frac {1}{16}} \\ \\ x = 1\qquad &\vee \qquad x = \frac {1}{2} \end{aligned} </math>
Dersom du sliter med algebra bør du kanskje holde deg til ABC-formelen, men dersom du har oversikt og har ambisjoner om god karakter (5,6), er metoden med fullstendig kvadrat noe du bør beherske.
Andregradslikninger på produktform
Man kan ha andregradslikninger på formen:
- <math>
\displaystyle (x + 1)(x – 2) = 0 </math>
Du ser at dette er en andregradslikning om du multipliserer ut parentesene:
- <math>
\displaystyle (x + 1)(x – 2) = x^2 - 2x + x – 2 = x^2 – x – 2 </math>
Man kan multiplisere ut faktorene som vist over og bruke ABC–formelen, men det finnes en mye enklere måte å løse likningen på:
Dersom produktet av to faktorer skal bli null, må en av faktorene være null.
Likningen $mn = 0$ medfører at $m$ eller $n$ må være lik null, om likningen skal være oppfylt.
I eksemplet
- <math>
\displaystyle (x + 1)(x – 2) = 0 </math>
betyr det at $x+1 = 0$ , eller at $x – 2 = 0$.
Det gir løsningene $x = -1$ og $x = 2$.
Problemet er redusert til løsninger av to enkle førstegradslikninger.
Faktorisering av andregradsuttrykk
Det generelle andregradsuttrykket er $ax^2 + bx + c.$ Ofte har man behov for å faktorisere uttrykket for å kunne forkorte og forenkle.
Man har følgende formel for faktorisering av andregradsuttrykk:
- <math>
\displaystyle ax^2 + bx + c = a( x-x_1)(x-x_2) </math>
Der $x_1$ og $x_2$ er løsninger av $ax^2 + bx + c = 0.$
Eksempel:
Faktoriser polynomet
- <math>
\displaystyle 6x^2-4x-2 </math>
Vi løser først likningen $6x^2-4x-2=0$ ved hjelp av ABC-formelen og får
- <math>
\displaystyle x_1 = 1 \qquad \vee \qquad x_2 = - \frac13 </math>
Så bruker vi formelen over og får:
- <math>
\displaystyle 6x^2-4x-2 = a(x-x_1)(x-x_2) = 6(x-1)(x + \frac 13) </math>
Denne fremgangsmåten er spesielt nyttig (helt nødvendig) når man skal forkorte brøker som inneholder andregradspolynomer.
Eksempel:
Skriv enklest mulig:
- <math>
\displaystyle \frac{6x^2-4x-2}{x + \frac13} </math>
Vi faktoriserer og får:
- <math>
\displaystyle \frac{6(x-1)(x + \frac 13)}{x + \frac13} = 6(x-1) </math>
Sum og produkt av røtter
Man har følgende sammenhenger mellom sum og produkt av røtter (løsninger):
En fullstendig andregradslikning skrives på formen
- <math>
\displaystyle ax^2 + bx + c = 0 </math>
Dersom $x_1$ og $x_2$ er røtter (løsninger) i likningen, så er
- <math>
\begin{aligned} x_1 + x_2 &= - \frac ba \\ \\ x_1 \cdot x_2 &= \frac ca \end{aligned} </math>
Eksempel:
Vi ønsker å finne et andregradsuttrykk som har røttene $x = -2$ og $x = 1$. Utover det har vi ingen andre krav.
Vi får:
- <math>
\begin{aligned} x_1 + x_2 &=- \frac ba \\ \\ -2 + 1 &= - \frac ba \\ \\ a &= b \end{aligned} </math>
Siden vi ikke har krav til koeffisientene kan vi jo velge $a = 1$. Da får vi at $a = 1$ og $b = 1$.
Produktet av røttene må oppfylle likningen
- <math>
\begin{aligned} x_1 \cdot x_2 &= \frac ca \\ \\ -2 \cdot 1 &= \frac ca \\ \\ c &= -2 \end{aligned} </math>
Vi får da likningen
- <math>
\displaystyle x^2 + x - 2 = 0 </math>
Ved å bruke ABC-formelen ser man at dette er en (av mange) likninger som har løsning for $x = 1$ og for $x = -2.$
Dersom man anvender disse formlene og finner en likning, må man sjekke at den virkelig har løsninger.
Irrasjonale likninger
Irrasjonale ligninger
Innledning
Dersom den ukjente i en ligning befinner seg under ett eller flere rottegn, sies ligningen å være irrasjonal.
Man må være fortrolig med bruk av kvadratsetningene og løsning av 2.gradsligninger før man arbeider med slike ligninger.
Falsk løsning
Irrasjonale ligninger løses vanligvis ved å kvadrere på begge sider av likhetstegnet.
Dette kan generere falske løsninger.
Du må derfor alltid sette prøve på svaret.
<math> x = -2
x^2 = (-2)^2
x^2 = 4 </math>
Løser man <math>x^2 = 4</math>, får man både <math>x = -2</math> og <math>x = 2</math>. Kvadreringen genererer altså en falsk løsning.
Eksempel 1
Før man kvadrerer skal rottegnet (og uttrykket under) stå alene på én side.
<math> \sqrt{x-2} = 4
(\sqrt{x-2})^2 = 4^2
x - 2 = 16
x = 18 </math>
Ved å sette prøve ser vi at <math>x = 18</math> er en løsning.
Eksempel 2
<math> \sqrt{x-2} = 3 - \sqrt{x+3}
\sqrt{x-2} + \sqrt{x+3} = 3
(\sqrt{x-2} + \sqrt{x+3})^2 = 9
x - 2 + 2\sqrt{x-2}\sqrt{x+3} + x + 3 = 9
2x + 1 + 2\sqrt{x-2}\sqrt{x+3} = 9
2\sqrt{x-2}\sqrt{x+3} = 8 - 2x
\sqrt{x-2}\sqrt{x+3} = 4 - x
(\sqrt{x-2}\sqrt{x+3})^2 = (4-x)^2
9x = 22
x = \frac{22}{9} </math>
Setter vi prøve, får vi lik verdi på begge sider. Dermed er <math>x = \frac{22}{9}</math> en løsning.
Eksempel 3
<math> x - \sqrt{3x+7} + 1 = 0
(-\sqrt{3x+7})^2 = (-x - 1)^2
3x + 7 = x^2 + 2x + 1
x^2 - x - 6 = 0
x = -2 \vee x = 3 </math>
Setter vi prøve, ser vi at <math>x = -2</math> ikke er løsning.
Løsningen er derfor:
<math>x = 3</math>
Eksempel 4
<math> \sqrt{2x + 10 + \sqrt{x+3}} = 5
2x + 10 + \sqrt{x+3} = 25
\sqrt{x+3} = 15 - 2x
x + 3 = 225 - 60x + 4x^2
4x^2 - 61x + 222 = 0
x = 6 \vee x = 9,25 </math>
Setter vi prøve, ser vi at kun <math>x = 6</math> er en løsning.
Trigonometriske likninger
Det finnes forskjellige typer trigonometriske likninger og ofte er det forskjellige måter å løse dem på. Nedenfor følger en oversikt over de vanligste typene og et forslag til hvordan de kan løses.
Det er viktig å ha enhetssirkelen i bakhodet og spesielt være klar over følgende:
- <math>\sin(x+2\pi)=\sin\,x</math>
- <math>\cos(x+2\pi)=\cos\,x</math>
- <math>\tan(x+\pi)=\tan\,x</math>
1. Trigonometriske grunnlikninger
Trigonometriske likninger som kun involverer én trigonometrisk funksjon, kaller vi trigonometriske grunnlikninger. Disse er de enkleste trigonometriske likningene å løse, og krever kun kunnskap om de trigonometriske funksjonenes inverser.
Løsningsmetode for trigonometriske grunnlikninger
Vi tar for oss ligningen
$a\sin(bx)=c$
Vi vil løse denne ligninger for <math>x</math>. Det første vi gjør er å isolere <math>\sin(bx)</math> på venstresiden:
$\sin(bx)=\frac ca$
Siden høyresiden er lik venstresiden, vil <math>\arcsin</math> av høyresiden være lik <math>\arcsin</math> av venstresiden. Altså:
$\arcsin(\sin(bx))=\arcsin(\frac ca)$ Dette gir oss to uttrykk for <math>x</math>:
$bx=\arcsin(\frac ca)\,\vee\,\pi-bx=\arcsin(\frac ca)$
Sinus er periodisk i <math>2\pi</math> så vi må legge til en vilkårlig multippel av <math>2\pi</math> på hver side.
<math>bx+k\cdot2\pi=\arcsin(\frac ca)\,\vee\,\pi-bx+k\cdot2\pi=\arcsin(\frac ca)\,,\,k\in\mathbb{Z}</math>
- Når vi isolerer <math>x</math> på venstresiden får vi
- <math>x=\frac{\arcsin(\frac ca)-k\cdot2\pi}{b}\,\vee\,x=\frac{\arcsin(\frac ca)-\pi(2k+1)}{b}\,,\,k\in\mathbb{Z}</math>
Den samme fremgangsmåten kan benyttes på trigonometriske grunnlikninger med <math>\cos</math> og <math>\tan</math> også, men husk at disse har litt forskjellige egenskaper, så løsningene blir ikke de samme.
EKSEMPEL 1.
COS
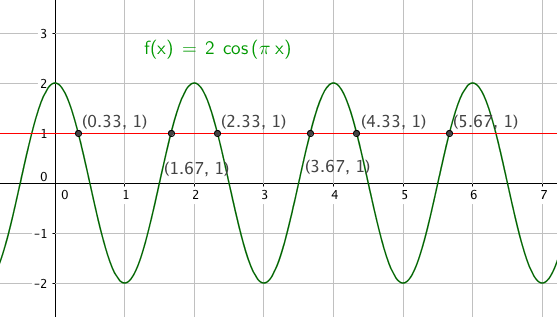
$2cos(\pi x)=1 \quad \quad \quad x\in [0, 2\pi> $
$cos( \pi x) = \frac 12 \\ \pi x = \frac{\pi}{3} +k2\pi \vee \pi x $
$= 2\pi-\frac{\pi}{3} + k2\pi \\ x= \frac 13+2k \vee x=2- \frac13 +2k \\ x= \frac 13 \vee x= \frac 73 \vee x= \frac{13}{3} \vee x= \frac 53 \vee x= \frac{11}{3} \vee x= \frac{17}{3}$
$x \in${$ \frac{1}{3}, \frac{5}{3}, \frac{7}{3}, \frac{11}{3}, \frac{13}{3}, \frac{17}{3}$}
Slik ser det ut:
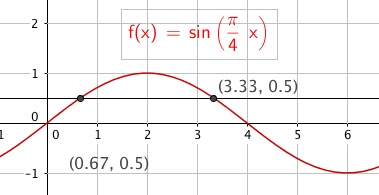
SIN
$sin( \frac{\pi}{4}x) = \frac 12 \quad \quad \quad x \in[0, 2 \pi> \\ \frac{\pi}{4}x = \frac{\pi}{6} +2k \pi \vee \frac{\pi}{4}x = \pi - \frac{\pi}{6} +2k \pi \\ x= \frac 23 +8k \vee x = 4- \frac 23 + 8k \\ x= \frac 23 \vee x = \frac{10}{3}$
$x \in ${$ \frac 23, \frac{10}{3}$}
Slik ser det ut:
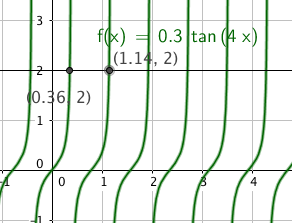
TAN
$0,3 tan(4x)= 2 \quad \quad \quad x \in [0, \frac{\pi}{2}> \\ tan(4x) = 6,667 \\ 4x = 1,42 + k \pi \\ x= 0,36 \vee x= 1,14$
$x \in ${ 0,36 , 1,14}
Slik ser det ut:
2)
$a cos^2 x + b cos x + c = 0 \quad $ eller $ \quad a sin^2 x + b sin x + c = 0$
Løses ved å erstatt cos x , eventuelt sin x, med u. Løser andregradsligningen og setter løsningen(e) lik cos x (eller sin x) og finner mulige x verdier.
Eksempel 2.
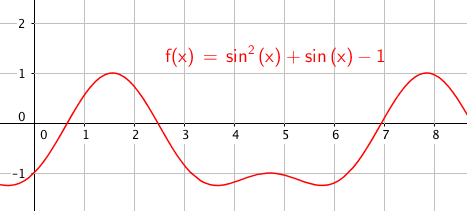
<math>\sin^2x+\sin\,x-1=0\,,\,x\in[0,2\pi></math>
Setter sin x = u og bruker andregradsformelen, og får:
<math>\sin\,x=\frac{\sqrt{5}-1}{2}</math>
<math>\sin\,x=\frac{\sqrt{5}+1}{2}</math>
Merk at <math>\frac{\sqrt{5}+1}{2}>1</math>, altså har ikke denne grunnlikningen noen løsninger.
Vi står igjen med kun den første trigonometriske grunnlikningen. Når vi løser denne, får vi
$x= 0,67 \vee x= 2,48$
Slik ser det ut:
$x \in${0,67 , 2,48}
3)
Begge sider divideres med cos x (forskjellig fra null). Vi får da en identitet i tan x.
Eksempel 3.
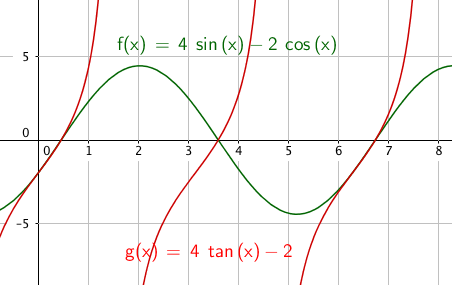
$4sinx-2cosx=0 \quad \quad x \in [0, 2 \pi>\\ 4tanx-2=0 \\ tanx = \frac 12 \\ x = tan^{-1}(\frac 12) = 0,46 + k \pi \\ x= 0,46 \vee x = 3,61$
$x \in$ {0,46 , 3,61}
Slik ser det ut:
4)
Ligningen løses ved å erstatte $sin^2x \quad $ med $1 - cos^2 x \quad$ eller $ cos^2 x \quad$ med $1 - sin^2 x$
Eksempel 4.
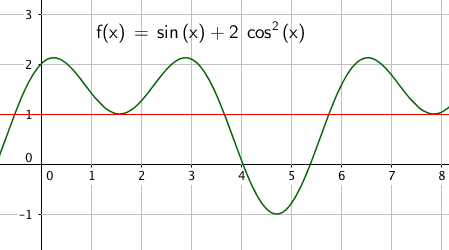
- <math>\sin\,x+2cos^2x=1\,,\,x\in[0,2\pi > </math>
- Vi kjenner identiteten <math>\sin^2x+\cos^2x=1</math>.
Den kan vi bruke her for å omforme ligningen til
- <math>\sin\,x+2-2\sin^2x=1</math>
- <math>2\sin^2x-\sin\,x-1=0</math>
- Dette er en andregradslikning i $\sin\,x$, som vi kan løse:
- <math>\sin\,x=\frac{1\pm\sqrt{1+8}}{4}=\frac{1\pm 3}{4}</math>
- <math>\sin\,x=\frac{1+3}{4}=1 \,\vee\,\sin\,x=\frac{1-3}{4}=-\frac12</math>
- <math>\sin\,x=1\,\Rightarrow\,x=\frac{\pi}{2}</math>
- <math>\sin\,x=-\frac12\,\Rightarrow\,x=\frac{7\pi}{6} \,\vee\,x=\frac{11\pi}{6}</math>
$x= \frac {\pi}{2} \vee x= \frac{7 \pi}{6} \vee x= \frac{11 \pi}{6}$
$x \in${$\frac {\pi}{2}, \frac{7 \pi}{6}, \frac{11 \pi}{6}$}
Slik ser det ut:
5)
Løses ved å dividere begge sider av likhetstegnet med $cos^2 x \quad \quad cos x \neq 0$
Eksempel 5.
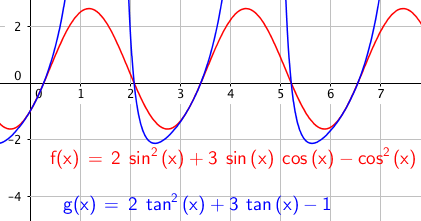
$2sin^2x+3sinxcosx - cos^2x=0 \quad x \in [0, 2\pi>\\ 2tan^2x+3tanx-1=0 \\ 2u^2+3u-1=0$
$tan x =-1,06 \vee tanx = 0,27 \\x= -1,06 + k\pi \vee x= 0,27 + k\pi \\ x = 0,27 \vee x=3,45 \vee x=2,08 \vee x=5,22 $
$x \in$ {0,27 , 2,08 , 3,45 , 5,22}
Slik ser det ut:
6)
Her må konstantleddet skrives om : $d = d \cdot 1 =d(sin^2 x + cos^2 x)$ . Ligningen løses nå som beskrevet i punktet over.
Eksempel 6.
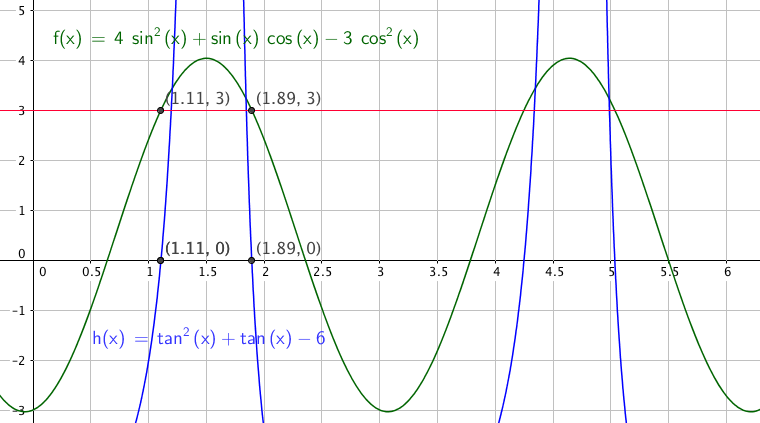
$4sin^2x+ sinx cos x - 3cos^2x=3 \quad \quad x \in [0, 2\pi> \\4sin^2x+ sinx cos x - 3cos^2x = 3sin^2x + 3cos^2x \\ sin^2x + sinx cosx - 6cos^2 =0 \\ tan^2x + tanx - 6 = 0 \\ tanx = -3 \vee tanx = 2 \\ x= -1,24 +k\pi \vee x=1,11 + k\pi \\ x= 1,11 \vee x= 4,25 \vee x= 1,90 \vee x=5,04 $
$x \in ${1,11 , 1,90 , 4,25 , 5,04}
Slik ser det ut:
7)
- <math>a\sin cx + bcos cx = d</math>
- <math> Asin (cx + \varphi)=d</math> der <math>A=\sqrt{a^2+b^2}</math> og <math>\varphi</math> er gitt ved <math> tan \varphi = \frac ba</math> og <math>\varphi</math>ligger i samme kvadrant som (a,b).
Eksempel 7.
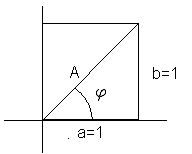
- Eksempel:
Vinkelen <math>\varphi</math> ligger i første kvadrant, <math>\varphi =tan^{-1}(1)= \frac {\pi}{4} </math>
Vi får$\sqrt 2 sin(x + \frac \pi 4) = 1 \\ sin (x+ \frac \pi 4) = \frac{\sqrt 2}{2} \\ x + \frac {\pi}{4} = \frac {\pi}{4} +2k\pi \vee x + \frac{\pi}{4}= \pi - \frac{\pi}{4} +2k\pi \\ x=0 \vee x= \frac {\pi}{2}$
$x \in$ {0, $\frac \pi 2$}
Det ser slik ut:
8)
$a^2\pm ab= 0 \Rightarrow a( a \pm b)= 0$
a og b er sinx og cosx, eler cosx og sinx.
Eksempel 8.
Når vi skal løse trigonometriske ligninger må vi ofte dele den opp i flere trigonometriske grunnlikninger før vi kan løse den. Et klassisk eksempel er faktoriseringsmetoden. Vi tar for oss ligningen
<math>\sin\,x\,\cos\,x-cos\,x=0\,,\,x\in [0,2\pi></math>
Selv om det kan være fristende, må du, uansett hva du gjør, ikke dele på <math>\cos\,x</math>. Generelt prøver man å ikke dele eller multiplisere med funksjoner av variabler, fordi du kan miste løsninger, eller lage falske løsninger. Dette gjelder generelt når du deler på null eller multipliserer med null. I stedet faktoriserer vi ligningen:
<math>\cos\,x\,(\sin\,x-1)=0</math>
- Nå ser vi at for at ligningen skal oppfylles, må <math>\cos\,x=0</math> eller <math>\sin\,x-1=0</math>. Vi har klart å redusere den kompositte trigonometriske ligningen til to trigonometriske grunnlikninger.
- <math>\sin\,x=1 \,\Rightarrow\, x=\frac{\pi}{2}</math>
- <math>\cos\,x=0 \,\Rightarrow\, x=\frac{\pi}{2} \,\vee\, x=\frac{3\pi}{2}</math>
$ x \in${$\frac{\pi}{2} , \frac{3\pi}{2}$}
- NB: Dersom du på forhånd har sjekket at det du deler eller multipliserer med ikke er lik null, er det greit å gjennomføre operasjonen. Dette kan gjøres ved å plugge inn null for den aktuelle faktoren og se om likningen oppfylles.